Published online by Cambridge University Press: 16 July 2019
We establish the first global results for groups definable in tame expansions of o-minimal structures. Let 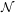 ${\mathcal{N}}$
be an expansion of an o-minimal structure
${\mathcal{N}}$
be an expansion of an o-minimal structure 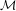 ${\mathcal{M}}$
that admits a good dimension theory. The setting includes dense pairs of o-minimal structures, expansions of
${\mathcal{M}}$
that admits a good dimension theory. The setting includes dense pairs of o-minimal structures, expansions of 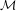 ${\mathcal{M}}$
by a Mann group, or by a subgroup of an elliptic curve, or a dense independent set. We prove: (1) a Weil’s group chunk theorem that guarantees a definable group with an o-minimal group chunk is o-minimal, (2) a full characterization of those definable groups that are o-minimal as those groups that have maximal dimension; namely, their dimension equals the dimension of their topological closure, (3) as an application, if
${\mathcal{M}}$
by a Mann group, or by a subgroup of an elliptic curve, or a dense independent set. We prove: (1) a Weil’s group chunk theorem that guarantees a definable group with an o-minimal group chunk is o-minimal, (2) a full characterization of those definable groups that are o-minimal as those groups that have maximal dimension; namely, their dimension equals the dimension of their topological closure, (3) as an application, if 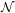 ${\mathcal{N}}$
expands
${\mathcal{N}}$
expands 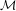 ${\mathcal{M}}$
by a dense independent set, then every definable group is o-minimal.
${\mathcal{M}}$
by a dense independent set, then every definable group is o-minimal.
The research was supported by an Independent Research Grant from the German Research Foundation (DFG) and a Zukunftskolleg Research Fellowship.