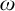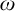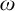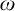1. Introduction
Keisler measures yield a natural notion of smallness for a definable subset of a structure: a subset X of
![]() $M^x$
defined by
$M^x$
defined by
![]() $\phi (x,a)$
is universally measure zero if it is assigned measure zero by every invariant Keisler measure on M. A more classical model theoretic notion of smallness is forking: dividing captures the idea that a small subset of a model can be “moved enough” by automorphisms so as to not overlap with itself. We are interested in comparing these notions of smallness in a sufficiently saturated and strongly homogeneous model.
$\phi (x,a)$
is universally measure zero if it is assigned measure zero by every invariant Keisler measure on M. A more classical model theoretic notion of smallness is forking: dividing captures the idea that a small subset of a model can be “moved enough” by automorphisms so as to not overlap with itself. We are interested in comparing these notions of smallness in a sufficiently saturated and strongly homogeneous model.
In stable theories, a definable set is universally measure zero if and only if it forks over
![]() $\emptyset $
[Reference Chernikov, Hrushovski, Kruckman, Krupiński, Moconja, Pillay and Ramsey3]. This is also the case in
$\emptyset $
[Reference Chernikov, Hrushovski, Kruckman, Krupiński, Moconja, Pillay and Ramsey3]. This is also the case in
![]() $\omega $
-categorical NIP theories [Reference Braunfeld, Jahel and Paolo2]. Until recently, it was unknown whether the two notions coincided in simple theories. The first counterexample, showing that in simple theories there can be non-forking formulas which are universally measure zero, is given in [Reference Chernikov, Hrushovski, Kruckman, Krupiński, Moconja, Pillay and Ramsey3]. Using the same technique, the authors also give examples of simple groups which are not definably amenable and prove some positive results in the context of small theories. Neither of the counterexamples given is
$\omega $
-categorical NIP theories [Reference Braunfeld, Jahel and Paolo2]. Until recently, it was unknown whether the two notions coincided in simple theories. The first counterexample, showing that in simple theories there can be non-forking formulas which are universally measure zero, is given in [Reference Chernikov, Hrushovski, Kruckman, Krupiński, Moconja, Pillay and Ramsey3]. Using the same technique, the authors also give examples of simple groups which are not definably amenable and prove some positive results in the context of small theories. Neither of the counterexamples given is
![]() $\omega $
-categorical. The theory of the first counterexample contains as a reduct the theory of the free action of the free group
$\omega $
-categorical. The theory of the first counterexample contains as a reduct the theory of the free action of the free group
![]() $\mathrm {F}_5$
on an infinite set, which has infinitely many
$\mathrm {F}_5$
on an infinite set, which has infinitely many
![]() $1$
-types over a single parameter. Meanwhile, on the definably amenable group case, all groups definable in an
$1$
-types over a single parameter. Meanwhile, on the definably amenable group case, all groups definable in an
![]() $\omega $
-categorical simple theory are definably amenable [Reference Chernikov, Hrushovski, Kruckman, Krupiński, Moconja, Pillay and Ramsey3, Corollary 4.14]. Indeed,
$\omega $
-categorical simple theory are definably amenable [Reference Chernikov, Hrushovski, Kruckman, Krupiński, Moconja, Pillay and Ramsey3, Corollary 4.14]. Indeed,
![]() $\omega $
-categorical supersimple groups are actually amenable being finite-by-abelian-by-finite [Reference Evans and Wagner10].
$\omega $
-categorical supersimple groups are actually amenable being finite-by-abelian-by-finite [Reference Evans and Wagner10].
It is natural to ask whether adding the assumption of
![]() $\omega $
-categoricity we can prove that being universally measure zero is the same as forking. Firstly, the known counterexample makes heavy use of a construction which is inherently not
$\omega $
-categoricity we can prove that being universally measure zero is the same as forking. Firstly, the known counterexample makes heavy use of a construction which is inherently not
![]() $\omega $
-categorical. Secondly,
$\omega $
-categorical. Secondly,
![]() $\omega $
-categoricity implies that any invariant Keisler measure is also definable, i.e., the set of parameters a for which
$\omega $
-categoricity implies that any invariant Keisler measure is also definable, i.e., the set of parameters a for which
![]() $\mu (\phi (x,a))=\alpha $
is
$\mu (\phi (x,a))=\alpha $
is
![]() $\emptyset $
-definable. In general, this is a substantially stronger assumption than invariance.
$\emptyset $
-definable. In general, this is a substantially stronger assumption than invariance.
Another motivation for an
![]() $\omega $
-categorical counterexample comes from the study of
$\omega $
-categorical counterexample comes from the study of
![]() $\omega $
-categorical
$\omega $
-categorical
![]() $MS$
-measurable structures [Reference Macpherson and Steinhorn16]. Until recently [Reference Evans8, Reference Marimon17], it was an open question whether all supersimple
$MS$
-measurable structures [Reference Macpherson and Steinhorn16]. Until recently [Reference Evans8, Reference Marimon17], it was an open question whether all supersimple
![]() $\omega $
-categorical structures of finite
$\omega $
-categorical structures of finite
![]() $SU$
-rank are
$SU$
-rank are
![]() $MS$
-measurable. Indeed, this question of Elwes and Macpherson [Reference Elwes, Macpherson, Chatzidakis, Macpherson, Pillay and Wilkie7] was the initial motivation for our study of Keisler measures in the context of
$MS$
-measurable. Indeed, this question of Elwes and Macpherson [Reference Elwes, Macpherson, Chatzidakis, Macpherson, Pillay and Wilkie7] was the initial motivation for our study of Keisler measures in the context of
![]() $\omega $
-categorical Hrushovski constructions. An
$\omega $
-categorical Hrushovski constructions. An
![]() $MS$
-measurable structure [Reference Macpherson and Steinhorn16] has a dimension-measure function which is definable, finite and such that the dimension and measures satisfy Fubini’s theorem. As we shall see in Lemma 4.8, forking and being universally measure zero yield the same notion of smallness in an
$MS$
-measurable structure [Reference Macpherson and Steinhorn16] has a dimension-measure function which is definable, finite and such that the dimension and measures satisfy Fubini’s theorem. As we shall see in Lemma 4.8, forking and being universally measure zero yield the same notion of smallness in an
![]() $MS$
-measurable context.
$MS$
-measurable context.
In this article, we show how for various classes of supersimple
![]() $\omega $
-categorical Hrushovski constructions we have formulas that do not fork over
$\omega $
-categorical Hrushovski constructions we have formulas that do not fork over
![]() $\emptyset $
but are universally measure zero:
$\emptyset $
but are universally measure zero:
Theorem 5.4. There are
![]() $\omega $
-categorical supersimple theories T of finite
$\omega $
-categorical supersimple theories T of finite
![]() $SU$
-rank with a formula
$SU$
-rank with a formula
![]() $\phi (x, a)$
which does not fork over the empty set, but which is universally measure zero.
$\phi (x, a)$
which does not fork over the empty set, but which is universally measure zero.
More generally, in Theorem 4.4, we show that if forking and being universally measure zero agree in a simple
![]() $\omega $
-categorical structure, then it must satisfy a stronger version of the independence theorem. It is easy to build
$\omega $
-categorical structure, then it must satisfy a stronger version of the independence theorem. It is easy to build
![]() $\omega $
-categorical Hrushovski constructions for which this fails. These structures are extremely amenable in the sense of [Reference Hrushovski, Krupiński and Pillay12], which implies the existence of invariant types, and so invariant Keisler measures, in each variable.
$\omega $
-categorical Hrushovski constructions for which this fails. These structures are extremely amenable in the sense of [Reference Hrushovski, Krupiński and Pillay12], which implies the existence of invariant types, and so invariant Keisler measures, in each variable.
We begin with Section 2, where we introduce ergodic measures and Keisler measures. Ergodic measures simplify our study since any measure can be considered as an “integral average” of them. Meanwhile, Keisler measures are the natural notion of a measure on a first-order structure. In Section 3, we study the
![]() $L^2$
-spaces associated with an invariant Keisler measure. From some results of Jahel and Tsankov [Reference Jahel and Tsankov13, Theorem 3.2 and Corollary 3.5], we know that in
$L^2$
-spaces associated with an invariant Keisler measure. From some results of Jahel and Tsankov [Reference Jahel and Tsankov13, Theorem 3.2 and Corollary 3.5], we know that in
![]() $\omega $
-categorical structures, ergodic measures are better behaved and a weak form of algebraic independence implies a form of probabilistic independence in the measure (Corollary 3.8). In Section 4, we show how in simple
$\omega $
-categorical structures, ergodic measures are better behaved and a weak form of algebraic independence implies a form of probabilistic independence in the measure (Corollary 3.8). In Section 4, we show how in simple
![]() $\omega $
-categorical structures with forking and being universally measure zero agreeing we have a stronger version of the independence theorem (Theorem 4.4). We conclude the section with some implications for
$\omega $
-categorical structures with forking and being universally measure zero agreeing we have a stronger version of the independence theorem (Theorem 4.4). We conclude the section with some implications for
![]() $MS$
-measurable structures. Finally, in Section 5, we give the example of an
$MS$
-measurable structures. Finally, in Section 5, we give the example of an
![]() $\omega $
-categorical structure, supersimple of finite
$\omega $
-categorical structure, supersimple of finite
![]() $SU$
-rank with a formula which does not fork over the empty set but which is universally measure zero.
$SU$
-rank with a formula which does not fork over the empty set but which is universally measure zero.
This article requires some knowledge in model theory. Chapters 1–4 of Tent and Ziegler’s book [Reference Tent and Ziegler22] should be sufficient, together with Chapter 16 of [Reference Poizat20] for understanding imaginaries and weak elimination of imaginaries. On simple theories, Chapters 2 and 3 of [Reference Kim14] cover the relevant definitions and results, including the definition of
![]() $SU$
-rank and the independence theorem. We also require some basic knowledge of Hilbert spaces and
$SU$
-rank and the independence theorem. We also require some basic knowledge of Hilbert spaces and
![]() $L^2$
-spaces, such as Chapter 1 of [Reference Conway5]. In Section 2 we give a self-contained introduction to ergodic measures and Keisler measures. The reader interested in
$L^2$
-spaces, such as Chapter 1 of [Reference Conway5]. In Section 2 we give a self-contained introduction to ergodic measures and Keisler measures. The reader interested in
![]() $MS$
-measurable structures should consult [Reference Macpherson and Steinhorn16] or [Reference Elwes, Macpherson, Chatzidakis, Macpherson, Pillay and Wilkie7]. This article does not require knowledge of Hrushovski constructions since all of the properties that we use are listed in Theorem 5.1. Further details about
$MS$
-measurable structures should consult [Reference Macpherson and Steinhorn16] or [Reference Elwes, Macpherson, Chatzidakis, Macpherson, Pillay and Wilkie7]. This article does not require knowledge of Hrushovski constructions since all of the properties that we use are listed in Theorem 5.1. Further details about
![]() $\omega $
-categorical Hrushovski constructions can be found in [Reference Wagner, Kaye and Macpherson24, Section 6.2.1], while [Reference Marimon17], especially in the Appendix, provides the details on the specific construction we give as an example in Theorem 5.4.
$\omega $
-categorical Hrushovski constructions can be found in [Reference Wagner, Kaye and Macpherson24, Section 6.2.1], while [Reference Marimon17], especially in the Appendix, provides the details on the specific construction we give as an example in Theorem 5.4.
To conclude, we provide some notation and conventions. Firstly, we work with a complete countable first-order
![]() $\mathcal {L}$
-theory T. From Section 3, by
$\mathcal {L}$
-theory T. From Section 3, by
![]() $\mathcal {M}$
we denote the countable model of an
$\mathcal {M}$
we denote the countable model of an
![]() $\omega $
-categorical theory. We write M for when we consider
$\omega $
-categorical theory. We write M for when we consider
![]() $\mathcal {M}$
as a set. We use greek letters
$\mathcal {M}$
as a set. We use greek letters
![]() $\phi , \psi , \chi , \dots $
to refer to formulas. The letters
$\phi , \psi , \chi , \dots $
to refer to formulas. The letters
![]() $x,y,z, \dots $
indicate variables, and may also indicate a finite tuple of variables. Similarly, the lowercase letters
$x,y,z, \dots $
indicate variables, and may also indicate a finite tuple of variables. Similarly, the lowercase letters
![]() $a,b,c, \dots $
indicate parameters from M, and may also indicate a finite tuple. Meanwhile, we indicate subsets of M by the uppercase
$a,b,c, \dots $
indicate parameters from M, and may also indicate a finite tuple. Meanwhile, we indicate subsets of M by the uppercase
![]() $A, B, C, \dots $
. For
$A, B, C, \dots $
. For
![]() $a, a'$
tuples from
$a, a'$
tuples from
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $A\subseteq M$
, we write
$A\subseteq M$
, we write
![]() $a\equiv _A a'$
to say that a and
$a\equiv _A a'$
to say that a and
![]() $a'$
have the same type over A.
$a'$
have the same type over A.
2. Keisler measures and ergodic measures
We begin with a brief and self-contained introduction to ergodic measures and Keisler measures. Firstly, we introduce ergodic measures in a general context. Then, we explain their utility for the study of Keisler measures.
2.1. Ergodic measures
Ergodic measures are an essential tool in our paper. They are better behaved than invariant measures and any invariant measure can be decomposed as an integral average of ergodic measures. Here we briefly introduce these measures and mention some basic results about them. Chapter 12 of Phelps’ book [Reference Phelps19] covers the theory we discuss at the adequate level of generality for our purposes.
We work in the context of a topological group G acting on a topological space X via a continuous action
![]() $\cdot :G\times X\to X$
. When X is compact and Hausdorff, we call this action a
$\cdot :G\times X\to X$
. When X is compact and Hausdorff, we call this action a
![]() ${G}$
-flow. Let
${G}$
-flow. Let
![]() $\mathcal {B}(X)$
be the set of Borel subsets of X, and let
$\mathcal {B}(X)$
be the set of Borel subsets of X, and let
![]() $\mu :\mathcal {B}(X)\to [0,1]$
be a Borel probability measure. We say that
$\mu :\mathcal {B}(X)\to [0,1]$
be a Borel probability measure. We say that
![]() $\mu $
is
$\mu $
is
![]() ${G}$
-invariant if for any
${G}$
-invariant if for any
![]() $\tau \in G$
and any
$\tau \in G$
and any
![]() $A\in \mathcal {B}(X)$
, we have that
$A\in \mathcal {B}(X)$
, we have that
![]() $\tau \cdot A\in \mathcal {B}(X)$
and
$\tau \cdot A\in \mathcal {B}(X)$
and
![]() $\mu (\tau \cdot A)=\mu (A)$
.
$\mu (\tau \cdot A)=\mu (A)$
.
Definition 2.1. We say that a G-invariant Borel probability measure
![]() $\mu $
is
$\mu $
is
![]() ${G}$
-ergodic if for all
${G}$
-ergodic if for all
![]() $A\in \mathcal {B}(X)$
, we have that if for all
$A\in \mathcal {B}(X)$
, we have that if for all
![]() $\tau \in G$
,
$\tau \in G$
,
then either
![]() $\mu (A)=0$
or
$\mu (A)=0$
or
![]() $\mu (A)=1$
.
$\mu (A)=1$
.
An alternative definition tells us that any invariant function is constant [Reference Einsiedler6, Proposition 2.14]:
Proposition 2.2. Let
![]() $(X, \mathcal {B}, \mu )$
be a probability space and G be a group acting on X such that
$(X, \mathcal {B}, \mu )$
be a probability space and G be a group acting on X such that
![]() $\mu $
is G-invariant. Then, the following are equivalent
$\mu $
is G-invariant. Then, the following are equivalent
![]() $:$
$:$
-
1. The measure
 $\mu $
is G-ergodic.
$\mu $
is G-ergodic. -
2. Any measurable function
 $f:X\to \mathbb {C}$
, which is G-invariant almost everywhere
$f:X\to \mathbb {C}$
, which is G-invariant almost everywhere
 $($
i.e., for any
$($
i.e., for any
 $\tau \in G, f\circ \tau =f$
a.e.
$\tau \in G, f\circ \tau =f$
a.e.
 $)$
is constant almost everywhere.
$)$
is constant almost everywhere.
We are interested in studying G-ergodic measures since, when X is metrizable, they yield an ergodic decomposition of any G-invariant measure. Hence, their study is essential to the understanding of the G-invariant measures on X. Below, for
![]() $f\in C(X, \mathbb {C})$
, we write
$f\in C(X, \mathbb {C})$
, we write
![]() $\mu (f)=\int _X f \mathrm {d}\mu $
. From [Reference Phelps19, p. 77] we have:
$\mu (f)=\int _X f \mathrm {d}\mu $
. From [Reference Phelps19, p. 77] we have:
Theorem 2.3 (Ergodic decomposition)
Let X be a compact metrizable space with a group G acting continuously on it. Let
![]() $\mu $
be a G-invariant Borel probability measure on X. Then, the space
$\mu $
be a G-invariant Borel probability measure on X. Then, the space
![]() $\mathfrak {M}(X)$
of G-invariant Borel probability measures on X is also metrizable and the set of G-ergodic measures
$\mathfrak {M}(X)$
of G-invariant Borel probability measures on X is also metrizable and the set of G-ergodic measures
![]() $\mathrm {Erg}(X)$
is a Borel subset of
$\mathrm {Erg}(X)$
is a Borel subset of
![]() $\mathfrak {M}(X)$
. Furthermore, there is a unique Borel probability measure
$\mathfrak {M}(X)$
. Furthermore, there is a unique Borel probability measure
![]() $\mathfrak {m}$
on
$\mathfrak {m}$
on
![]() $\mathfrak {M}(X)$
such that for any
$\mathfrak {M}(X)$
such that for any
![]() $f\in C(X, \mathbb {C})$
,
$f\in C(X, \mathbb {C})$
,
 $$\begin{align*}\mu(f)=\int_{\mathrm{Erg}(X)} \nu(f) \mathrm{d}\mathfrak{m}(\nu).\end{align*}$$
$$\begin{align*}\mu(f)=\int_{\mathrm{Erg}(X)} \nu(f) \mathrm{d}\mathfrak{m}(\nu).\end{align*}$$
2.2. Keisler measures
Keisler measures are finitely additive probability measures on the space of definable subsets of a structure. Chapter 7 of Simon’s book [Reference Simon21] is a good introduction to the subject. We give a brief self-contained discussion and note the importance of ergodic measures in the study of invariant Keisler measures.
Let T be a complete
![]() $\mathcal {L}$
-theory, where
$\mathcal {L}$
-theory, where
![]() $\mathcal {L}$
is a countable first-order language and
$\mathcal {L}$
is a countable first-order language and
![]() $\mathcal {M}\models T$
. Let
$\mathcal {M}\models T$
. Let
![]() $\mathrm {Def}_x(M)$
denote the Boolean algebra of
$\mathrm {Def}_x(M)$
denote the Boolean algebra of
![]() $\mathcal {L}(M)$
-formulas in the free variable x up to
$\mathcal {L}(M)$
-formulas in the free variable x up to
![]() $\mathrm {Th}(\mathcal {M}_M)$
-equivalence, where
$\mathrm {Th}(\mathcal {M}_M)$
-equivalence, where
![]() $\mathcal {M}_M$
is the expansion of
$\mathcal {M}_M$
is the expansion of
![]() $\mathcal {M}$
by constant symbols for each element of M. Let
$\mathcal {M}$
by constant symbols for each element of M. Let
![]() $S_x(M)$
be the Stone space of types over M in the variable x with the usual topology. We write
$S_x(M)$
be the Stone space of types over M in the variable x with the usual topology. We write
![]() $[\phi (x,a)]$
for the clopen set of types containing the formula
$[\phi (x,a)]$
for the clopen set of types containing the formula
![]() $\phi (x,a)$
.
$\phi (x,a)$
.
This space is always compact and Hausdorff. Moreover, when M is countable, it is also metrizable. This can be seen by taking an enumeration of the
![]() $\mathcal {L}(M)$
-formulas
$\mathcal {L}(M)$
-formulas
![]() $\phi _1, \phi _2, \dots $
and then for
$\phi _1, \phi _2, \dots $
and then for
![]() $p_1, p_2\in S_x(M),$
letting
$p_1, p_2\in S_x(M),$
letting
![]() $d(p_1,p_2)=\frac {1}{2^n}$
, where n is the smallest natural number such that
$d(p_1,p_2)=\frac {1}{2^n}$
, where n is the smallest natural number such that
![]() $\phi _n$
is not contained in both
$\phi _n$
is not contained in both
![]() $p_1$
and
$p_1$
and
![]() $p_2$
. The automorphism group
$p_2$
. The automorphism group
![]() $\mathrm {Aut}(M)$
naturally acts on
$\mathrm {Aut}(M)$
naturally acts on
![]() $\mathrm {Def}_x(M)$
and on
$\mathrm {Def}_x(M)$
and on
![]() $S_x(M)$
, where for
$S_x(M)$
, where for
![]() $\tau \in \mathrm {Aut}(M)$
,
$\tau \in \mathrm {Aut}(M)$
,
![]() $\tau \cdot \phi (x, a)=\phi (x, \tau (a))$
and for
$\tau \cdot \phi (x, a)=\phi (x, \tau (a))$
and for
![]() $p\in S_x(M)$
,
$p\in S_x(M)$
,
Definition 2.4. Let
![]() $\mathcal {M}$
be an
$\mathcal {M}$
be an
![]() $\mathcal {L}$
-structure. We say that
$\mathcal {L}$
-structure. We say that
![]() $\mu :\mathrm {Def}_x(M)\to [0,1]$
is a Keisler measure if it is a finitely additive measure such that
$\mu :\mathrm {Def}_x(M)\to [0,1]$
is a Keisler measure if it is a finitely additive measure such that
![]() $\mu (x=x)=1$
. We say that
$\mu (x=x)=1$
. We say that
![]() $\mu $
is
$\mu $
is
![]() $\mathrm {Aut}(M)$
-invariant if for any
$\mathrm {Aut}(M)$
-invariant if for any
![]() $\tau \in \mathrm {Aut}(M)$
,
$\tau \in \mathrm {Aut}(M)$
,
For an infinite cardinal
![]() $\kappa $
, we say that
$\kappa $
, we say that
![]() $\mathcal {M}$
is strongly
$\mathcal {M}$
is strongly
![]() $\boldsymbol {\kappa }$
-homogeneous if whenever a and
$\boldsymbol {\kappa }$
-homogeneous if whenever a and
![]() $a'$
are tuples of cardinality
$a'$
are tuples of cardinality
![]() $<\kappa $
such that
$<\kappa $
such that
![]() $a\equiv a'$
, there is
$a\equiv a'$
, there is
![]() $\tau \in \mathrm {Aut}(M)$
such that
$\tau \in \mathrm {Aut}(M)$
such that
![]() $\tau (a)=a'$
. If
$\tau (a)=a'$
. If
![]() $\mathcal {M}$
is strongly
$\mathcal {M}$
is strongly
![]() $\omega $
-homogeneous, for a Keisler measure to be
$\omega $
-homogeneous, for a Keisler measure to be
![]() $\mathrm {Aut}(M)$
-invariant is equivalent to saying that, if
$\mathrm {Aut}(M)$
-invariant is equivalent to saying that, if
![]() $a\equiv a'$
, then
$a\equiv a'$
, then
![]() $\mu (\phi (x, a))=\mu (\phi (x, a'))$
.
$\mu (\phi (x, a))=\mu (\phi (x, a'))$
.
As noted in the introduction, Keisler measures give us a natural notion of smallness for a definable set.
Definition 2.5. Let
![]() $\mathcal {M}$
be
$\mathcal {M}$
be
![]() $\omega $
-saturated and strongly
$\omega $
-saturated and strongly
![]() $\omega $
-homogeneous. We say that
$\omega $
-homogeneous. We say that
![]() $\phi (x, b)\in \mathrm {Def}_x(M)$
is universally measure zero if
$\phi (x, b)\in \mathrm {Def}_x(M)$
is universally measure zero if
![]() $\mu (\phi (x,b))=0$
for every
$\mu (\phi (x,b))=0$
for every
![]() $\mathrm {Aut}(M)$
-invariant Keisler measure. Similarly, let
$\mathrm {Aut}(M)$
-invariant Keisler measure. Similarly, let
![]() $A\subseteq M$
and let
$A\subseteq M$
and let
![]() $\mathcal {M}$
be
$\mathcal {M}$
be
![]() $\kappa $
-saturated and strongly
$\kappa $
-saturated and strongly
![]() $\kappa $
-homogeneous for
$\kappa $
-homogeneous for
![]() $\kappa =\max \{|A|^+, \omega \}$
. We say that
$\kappa =\max \{|A|^+, \omega \}$
. We say that
![]() $\phi (x, b)\in \mathrm {Def}_x(M)$
is universally measure zero over
$\phi (x, b)\in \mathrm {Def}_x(M)$
is universally measure zero over
![]() ${A}$
if it is assigned measure zero by every
${A}$
if it is assigned measure zero by every
![]() $\mathrm {Aut}(M/A)$
-invariant Keisler measure. We call
$\mathrm {Aut}(M/A)$
-invariant Keisler measure. We call
![]() $\mathcal {O}(A)$
the set of formulas in
$\mathcal {O}(A)$
the set of formulas in
![]() $\mathrm {Def}_x(M)$
which are universally measure zero over A.
$\mathrm {Def}_x(M)$
which are universally measure zero over A.
The set
![]() $\mathcal {O}_x(A)=\mathcal {O}(A)\cap \mathrm {Def}_x(M)$
forms an ideal in the Boolean algebra of
$\mathcal {O}_x(A)=\mathcal {O}(A)\cap \mathrm {Def}_x(M)$
forms an ideal in the Boolean algebra of
![]() $\mathrm {Def}_x(M)$
[Reference Chernikov, Hrushovski, Kruckman, Krupiński, Moconja, Pillay and Ramsey3]. Similarly,
$\mathrm {Def}_x(M)$
[Reference Chernikov, Hrushovski, Kruckman, Krupiński, Moconja, Pillay and Ramsey3]. Similarly,
![]() $F_x(A)$
, the set of formulas in the variable x with parameters from M forking over A, also forms an ideal. Our main result is that there are
$F_x(A)$
, the set of formulas in the variable x with parameters from M forking over A, also forms an ideal. Our main result is that there are
![]() $\omega $
-categorical supersimple theories for which
$\omega $
-categorical supersimple theories for which
![]() $\mathcal {O}(\emptyset )$
strictly contains the set of formulas forking over
$\mathcal {O}(\emptyset )$
strictly contains the set of formulas forking over
![]() $\emptyset $
,
$\emptyset $
,
![]() $F(\emptyset )$
.
$F(\emptyset )$
.
Remark 2.6. In other articles [Reference Chernikov, Hrushovski, Kruckman, Krupiński, Moconja, Pillay and Ramsey3], being universally measure zero is defined in the monster model for the theory. In this article, since we work over finite sets, no generality is lost by focusing on an
![]() $\omega $
-saturated strongly
$\omega $
-saturated strongly
![]() $\omega $
-homogeneous model. In fact, if
$\omega $
-homogeneous model. In fact, if
![]() $F(\emptyset )=\mathcal {O}(\emptyset )$
in an
$F(\emptyset )=\mathcal {O}(\emptyset )$
in an
![]() $\omega $
-saturated strongly
$\omega $
-saturated strongly
![]() $\omega $
-homogeneous model of T, this is the case in all such models (cf. [Reference Hrushovski, Krupiński and Pillay12, Proposition 2.3]). In particular, we may focus on invariant Keisler measures on the countable model of the
$\omega $
-homogeneous model of T, this is the case in all such models (cf. [Reference Hrushovski, Krupiński and Pillay12, Proposition 2.3]). In particular, we may focus on invariant Keisler measures on the countable model of the
![]() $\omega $
-categorical theory we are studying. More generally, whenever we compare the sizes of
$\omega $
-categorical theory we are studying. More generally, whenever we compare the sizes of
![]() $F(A)$
and
$F(A)$
and
![]() $\mathcal {O}(A)$
in this article we always work over a sufficiently saturated and strongly homogeneous model.
$\mathcal {O}(A)$
in this article we always work over a sufficiently saturated and strongly homogeneous model.
A Keisler measure
![]() $\mu $
can be extended uniquely to a regular
$\mu $
can be extended uniquely to a regular
![]() $\sigma $
-additive Borel probability measure
$\sigma $
-additive Borel probability measure
![]() $\mu : \mathcal {B}_x(M)\to [0,1]$
, where
$\mu : \mathcal {B}_x(M)\to [0,1]$
, where
![]() $\mathcal {B}_x(M)$
is the set of Borel subsets of
$\mathcal {B}_x(M)$
is the set of Borel subsets of
![]() $S_x(M)$
[Reference Simon21, Section 7.1]. Conversely, any regular Borel probability measure on
$S_x(M)$
[Reference Simon21, Section 7.1]. Conversely, any regular Borel probability measure on
![]() $S_x(M)$
induces a Keisler measure by considering its restriction to clopen sets. This correspondence still holds between
$S_x(M)$
induces a Keisler measure by considering its restriction to clopen sets. This correspondence still holds between
![]() $\mathrm {Aut}(M)$
-invariant Keisler measures in the variable x and
$\mathrm {Aut}(M)$
-invariant Keisler measures in the variable x and
![]() $\mathrm {Aut}(M)$
-invariant regular Borel probability measures on
$\mathrm {Aut}(M)$
-invariant regular Borel probability measures on
![]() $S_x(M)$
. From here, we shall speak interchangeably of the two.
$S_x(M)$
. From here, we shall speak interchangeably of the two.
Remark 2.7. An
![]() $\mathrm {Aut}(M^{eq})$
-invariant Keisler measure
$\mathrm {Aut}(M^{eq})$
-invariant Keisler measure
![]() $\mu ^{eq}$
on
$\mu ^{eq}$
on
![]() $\mathcal {M}^{eq}$
in the real variable x is entirely determined by its restriction to its induced
$\mathcal {M}^{eq}$
in the real variable x is entirely determined by its restriction to its induced
![]() $\mathrm {Aut}(M)$
-invariant Keisler measure
$\mathrm {Aut}(M)$
-invariant Keisler measure
![]() $\mu $
on
$\mu $
on
![]() $\mathcal {M}$
. Furthermore,
$\mathcal {M}$
. Furthermore,
![]() $\mu ^{eq}$
is ergodic if and only if
$\mu ^{eq}$
is ergodic if and only if
![]() $\mu $
is.
$\mu $
is.
If we are interested in studying the universally measure zero formulas for a countable structure, it is helpful to study
![]() $\mathrm {Aut}(M)$
-ergodic measures on
$\mathrm {Aut}(M)$
-ergodic measures on
![]() $S_x(M)$
. From the ergodic decomposition 2.3, we get:
$S_x(M)$
. From the ergodic decomposition 2.3, we get:
Corollary 2.8. Let
![]() $\mathcal {M}$
be a countable structure and let
$\mathcal {M}$
be a countable structure and let
![]() $\mu $
be an
$\mu $
be an
![]() $\mathrm {Aut}(M)$
-invariant Borel probability measure on
$\mathrm {Aut}(M)$
-invariant Borel probability measure on
![]() $S_x(M)$
. Let
$S_x(M)$
. Let
![]() $\mathfrak {M}_x(M)$
be the space of
$\mathfrak {M}_x(M)$
be the space of
![]() $\mathrm {Aut}(M)$
-invariant Borel probability measures on
$\mathrm {Aut}(M)$
-invariant Borel probability measures on
![]() $S_x(M)$
. Then, there is a unique Borel probability measure
$S_x(M)$
. Then, there is a unique Borel probability measure
![]() $\mathfrak {m}$
on
$\mathfrak {m}$
on
![]() $\mathfrak {M}_x(M)$
such that for any
$\mathfrak {M}_x(M)$
such that for any
![]() $\mathcal {L}(M)$
-formula
$\mathcal {L}(M)$
-formula
![]() $\phi (x,a)$
,
$\phi (x,a)$
,
 $$\begin{align*}\mu([\phi(x,a)])=\int_{\mathrm{Erg}_x(M)} \nu([\phi(x,a)]) \mathrm{d}\mathfrak{m}(\nu),\end{align*}$$
$$\begin{align*}\mu([\phi(x,a)])=\int_{\mathrm{Erg}_x(M)} \nu([\phi(x,a)]) \mathrm{d}\mathfrak{m}(\nu),\end{align*}$$
where
![]() $\mathrm {Erg}_x(M)$
is the space of
$\mathrm {Erg}_x(M)$
is the space of
![]() $\mathrm {Aut}(M)$
-ergodic measures.
$\mathrm {Aut}(M)$
-ergodic measures.
Remark 2.9. When M is countable, every Borel measure
![]() $\mu $
on
$\mu $
on
![]() $S_x(M)$
is regular [Reference Bogachev1, Theorem 7.1.7]. From [Reference Evans and Tsankov9, Corollary 1.2], we actually know that when
$S_x(M)$
is regular [Reference Bogachev1, Theorem 7.1.7]. From [Reference Evans and Tsankov9, Corollary 1.2], we actually know that when
![]() $\mathcal {M}$
is the countable model of an
$\mathcal {M}$
is the countable model of an
![]() $\omega $
-categorical theory,
$\omega $
-categorical theory,
![]() $\mathrm {Erg}_x(M)$
is closed in the space
$\mathrm {Erg}_x(M)$
is closed in the space
![]() $\mathfrak {M}_x(M)$
.
$\mathfrak {M}_x(M)$
.
For conciseness of notation, in subsequent sections we shall generally refer to
![]() $\mu $
as an ergodic measure on
$\mu $
as an ergodic measure on
![]() $\mathcal {M}^{eq}$
(in the variable x). By this we mean that
$\mathcal {M}^{eq}$
(in the variable x). By this we mean that
![]() $\mu $
is a Borel probability measure on
$\mu $
is a Borel probability measure on
![]() $S_x(M^{eq})$
invariant under the action of
$S_x(M^{eq})$
invariant under the action of
![]() $\mathrm {Aut}(M^{eq})$
, which is also
$\mathrm {Aut}(M^{eq})$
, which is also
![]() $\mathrm {Aut}(M^{eq})$
-ergodic. As noted above, when x is a variable in the real sort, there is a one-to-one correspondence between these ergodic measures and the ergodic
$\mathrm {Aut}(M^{eq})$
-ergodic. As noted above, when x is a variable in the real sort, there is a one-to-one correspondence between these ergodic measures and the ergodic
![]() $\mathrm {Aut}(M)$
-invariant Borel probability measures on
$\mathrm {Aut}(M)$
-invariant Borel probability measures on
![]() $S_x(M)$
. More generally, given the various correspondences explained in this section we can safely use
$S_x(M)$
. More generally, given the various correspondences explained in this section we can safely use
![]() $\mu $
to denote both the Keisler measure and the corresponding Borel probability measures on
$\mu $
to denote both the Keisler measure and the corresponding Borel probability measures on
![]() $S_x(M)$
and
$S_x(M)$
and
![]() $S_x(M^{eq})$
.
$S_x(M^{eq})$
.
3. Weak algebraic independence and probabilistic independence
Given the Borel probability space
![]() $(S_x(M^{eq}), \mathcal {B}_x(M^{eq}), \mu )$
induced by an invariant Keisler measure on M in the variable x, we wish to study the associated Hilbert space
$(S_x(M^{eq}), \mathcal {B}_x(M^{eq}), \mu )$
induced by an invariant Keisler measure on M in the variable x, we wish to study the associated Hilbert space
![]() $L^2(\mu )$
. In this section we introduce some of the relevant tools for this, following the discussion of [Reference Jahel and Tsankov13, Reference Tsankov23]. Furthermore, we shall show how various results of [Reference Jahel and Tsankov13] yield that a weak form of algebraic independence between parameters implies a form of probabilistic independence in an ergodic measure. This result is Corollary 3.8.
$L^2(\mu )$
. In this section we introduce some of the relevant tools for this, following the discussion of [Reference Jahel and Tsankov13, Reference Tsankov23]. Furthermore, we shall show how various results of [Reference Jahel and Tsankov13] yield that a weak form of algebraic independence between parameters implies a form of probabilistic independence in an ergodic measure. This result is Corollary 3.8.
Let
![]() $\mathcal {M}$
be a countable
$\mathcal {M}$
be a countable
![]() $\omega $
-categorical structure. We have that
$\omega $
-categorical structure. We have that
![]() $\mathrm {Aut}(M)$
is a Polish group, that is, a separable completely metrizable topological group. In particular, in the topology of
$\mathrm {Aut}(M)$
is a Polish group, that is, a separable completely metrizable topological group. In particular, in the topology of
![]() $G=\mathrm {Aut}(M)$
, the pointwise stabilizers of finite sets
$G=\mathrm {Aut}(M)$
, the pointwise stabilizers of finite sets
![]() $G_A=\mathrm {Aut}(M/A)$
for
$G_A=\mathrm {Aut}(M/A)$
for
![]() $A\subset M$
finite, are neighbourhoods of the identity and the set of cosets of these pointwise stabilizers form a basis of open sets for the topology [Reference Macpherson15, Section 4.1].
$A\subset M$
finite, are neighbourhoods of the identity and the set of cosets of these pointwise stabilizers form a basis of open sets for the topology [Reference Macpherson15, Section 4.1].
Definition 3.1. Let
![]() $\mathcal {H}$
be a complex Hilbert space and
$\mathcal {H}$
be a complex Hilbert space and
![]() $U(\mathcal {H})$
be its unitary group. A unitary representation of a topological group G is a continuous action of G on
$U(\mathcal {H})$
be its unitary group. A unitary representation of a topological group G is a continuous action of G on
![]() $\mathcal {H}$
by unitary operators. Equivalently, we may say that it is a homomorphism
$\mathcal {H}$
by unitary operators. Equivalently, we may say that it is a homomorphism
![]() $\pi : G\to U(\mathcal {H})$
such that for each
$\pi : G\to U(\mathcal {H})$
such that for each
![]() $f\in \mathcal {H}$
the map
$f\in \mathcal {H}$
the map
![]() $\tau \mapsto \pi (\tau )\cdot f$
is continuous.
$\tau \mapsto \pi (\tau )\cdot f$
is continuous.
As noted in the previous section, a Keisler measure
![]() $\mu $
on
$\mu $
on
![]() $\mathcal {M}$
in the variable x induces a Borel probability space
$\mathcal {M}$
in the variable x induces a Borel probability space
![]() $(S_x(M^{eq}), \mathcal {B}_x(M^{eq}), \mu )$
. We are interested in studying the complex
$(S_x(M^{eq}), \mathcal {B}_x(M^{eq}), \mu )$
. We are interested in studying the complex
![]() $L^2$
-space
$L^2$
-space
![]() $L^2(S_x(M^{eq}), \mathcal {B}_x(M^{eq}), \mu )$
, which we abbreviate
$L^2(S_x(M^{eq}), \mathcal {B}_x(M^{eq}), \mu )$
, which we abbreviate
![]() $L^2(\mu )$
.
$L^2(\mu )$
.
The action of
![]() $\mathrm {Aut}(M)$
on M naturally induces an action
$\mathrm {Aut}(M)$
on M naturally induces an action
![]() $\lambda : \mathrm {Aut}(M)\times L^2(\mu )\to L^2(\mu )$
, where for
$\lambda : \mathrm {Aut}(M)\times L^2(\mu )\to L^2(\mu )$
, where for
![]() $\sigma \in \mathrm {Aut}(M), f\in L^2(\mu )$
,
$\sigma \in \mathrm {Aut}(M), f\in L^2(\mu )$
,
This action is well defined and preserves integrals. For each
![]() $\sigma \in \mathrm {Aut}(M)$
, the map
$\sigma \in \mathrm {Aut}(M)$
, the map
![]() $\Lambda _\sigma :L^2(\mu )\to L^2(\mu )$
given by
$\Lambda _\sigma :L^2(\mu )\to L^2(\mu )$
given by
![]() $f\mapsto \lambda (\sigma , f)$
is a unitary operator. Moreover, the map
$f\mapsto \lambda (\sigma , f)$
is a unitary operator. Moreover, the map
![]() $\pi : \mathrm {Aut}(M) \to U(L^2(\mu ))$
from the group of automorphisms of M to the group of unitary operators of
$\pi : \mathrm {Aut}(M) \to U(L^2(\mu ))$
from the group of automorphisms of M to the group of unitary operators of
![]() $L^2(\mu )$
given by
$L^2(\mu )$
given by
![]() $\sigma \mapsto \Lambda _\sigma $
is a unitary representation (cf. Section 3 of [Reference Tsankov23]).
$\sigma \mapsto \Lambda _\sigma $
is a unitary representation (cf. Section 3 of [Reference Tsankov23]).
Let
![]() $\mathcal {H}$
be a complex Hilbert space and the action of
$\mathcal {H}$
be a complex Hilbert space and the action of
![]() $G=\mathrm {Aut}(M)$
on
$G=\mathrm {Aut}(M)$
on
![]() $\mathcal {H}$
be a unitary representation. For
$\mathcal {H}$
be a unitary representation. For
![]() $A\subseteq M^{eq}$
we write, following [Reference Jahel and Tsankov13],
$A\subseteq M^{eq}$
we write, following [Reference Jahel and Tsankov13],
where for
![]() $S\subset \mathcal {H}$
,
$S\subset \mathcal {H}$
,
![]() $\overline {S}$
is its closure.
$\overline {S}$
is its closure.
Definition 3.2. Let
![]() $\mathcal {H}$
be a Hilbert space and
$\mathcal {H}$
be a Hilbert space and
![]() $\mathcal {K}\subseteq \mathcal {H}$
be a subspace. We denote the orthogonal complement of
$\mathcal {K}\subseteq \mathcal {H}$
be a subspace. We denote the orthogonal complement of
![]() $\mathcal {K}$
in
$\mathcal {K}$
in
![]() $\mathcal {H}$
(often denoted as
$\mathcal {H}$
(often denoted as
![]() $\mathcal {K}^\perp $
) as
$\mathcal {K}^\perp $
) as
![]() $\mathcal {H}\ominus \mathcal {K}$
. When
$\mathcal {H}\ominus \mathcal {K}$
. When
![]() $\mathcal {K}$
is a closed subspace, we have that
$\mathcal {K}$
is a closed subspace, we have that
![]() $\mathcal {H}=\mathcal {K}\oplus (\mathcal {H}\ominus \mathcal {K})$
. Given subspaces
$\mathcal {H}=\mathcal {K}\oplus (\mathcal {H}\ominus \mathcal {K})$
. Given subspaces
![]() $\mathcal {H}_0, \mathcal {H}_1, \mathcal {H}_2\subseteq \mathcal {H}$
, and
$\mathcal {H}_0, \mathcal {H}_1, \mathcal {H}_2\subseteq \mathcal {H}$
, and
![]() $\mathcal {H}_0\subseteq \mathcal {H}_i$
for
$\mathcal {H}_0\subseteq \mathcal {H}_i$
for
![]() $i\in \{1,2\}$
we say that
$i\in \{1,2\}$
we say that
![]() $\mathcal {H}_1$
and
$\mathcal {H}_1$
and
![]() $\mathcal {H}_2$
are orthogonal over
$\mathcal {H}_2$
are orthogonal over
![]() $\mathcal {H}_0$
and write
$\mathcal {H}_0$
and write
![]() $\mathcal {H}_1\perp _{\mathcal {H}_0}\mathcal {H}_2$
if
$\mathcal {H}_1\perp _{\mathcal {H}_0}\mathcal {H}_2$
if
![]() $(\mathcal {H}_1\ominus \mathcal {H}_0)\perp (\mathcal {H}_2\ominus \mathcal {H}_0)$
.
$(\mathcal {H}_1\ominus \mathcal {H}_0)\perp (\mathcal {H}_2\ominus \mathcal {H}_0)$
.
Note that when the
![]() $\mathcal {H}_i$
are all closed subspaces for
$\mathcal {H}_i$
are all closed subspaces for
![]() $i\in \{1, 2, 3\}$
with
$i\in \{1, 2, 3\}$
with
![]() $\mathcal {H}_1\perp _{\mathcal {H}_0}\mathcal {H}_2$
, we have that for
$\mathcal {H}_1\perp _{\mathcal {H}_0}\mathcal {H}_2$
, we have that for
![]() $f\in \mathcal {H}_1$
we can decompose f into
$f\in \mathcal {H}_1$
we can decompose f into
![]() $f=f_1+f_0$
, where
$f=f_1+f_0$
, where
![]() $f'\in \mathcal {H}_1\ominus \mathcal {H}_0$
and
$f'\in \mathcal {H}_1\ominus \mathcal {H}_0$
and
![]() $f_0\in \mathcal {H}_0$
. Similarly, for
$f_0\in \mathcal {H}_0$
. Similarly, for
![]() $g\in \mathcal {H}_2$
we can decompose it as
$g\in \mathcal {H}_2$
we can decompose it as
![]() $g=g_2+g_0$
. Now, by the orthogonalities
$g=g_2+g_0$
. Now, by the orthogonalities
![]() $(\mathcal {H}_i\ominus \mathcal {H}_0)\perp \mathcal {H}_0$
for
$(\mathcal {H}_i\ominus \mathcal {H}_0)\perp \mathcal {H}_0$
for
![]() $i\in \{1,2\}$
and
$i\in \{1,2\}$
and
![]() $(\mathcal {H}_1\ominus \mathcal {H}_0)\perp (\mathcal {H}_2\ominus \mathcal {H}_0)$
, we have that
$(\mathcal {H}_1\ominus \mathcal {H}_0)\perp (\mathcal {H}_2\ominus \mathcal {H}_0)$
, we have that
where
![]() $\langle \cdot , \cdot \rangle $
is the inner product on
$\langle \cdot , \cdot \rangle $
is the inner product on
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
In an
![]() $\omega $
-categorical structure, we have the following theorem of Jahel and Tsankov, which translates weak algebraic independence into orthogonality of the associated Hilbert spaces:
$\omega $
-categorical structure, we have the following theorem of Jahel and Tsankov, which translates weak algebraic independence into orthogonality of the associated Hilbert spaces:
Theorem 3.3 [Reference Jahel and Tsankov13, Theorem 3.2]
Let M be
![]() $\omega $
-categorical and
$\omega $
-categorical and
![]() $G=\mathrm {Aut}(M)$
. Let
$G=\mathrm {Aut}(M)$
. Let
![]() $A, B\subseteq M^{eq}$
be algebraically closed with respect to
$A, B\subseteq M^{eq}$
be algebraically closed with respect to
![]() $\mathrm {acl}^{eq}$
. Then,
$\mathrm {acl}^{eq}$
. Then,
![]() $\mathcal {H}_A\perp _{\mathcal {H}_{A\cap B}}\mathcal {H}_B$
.
$\mathcal {H}_A\perp _{\mathcal {H}_{A\cap B}}\mathcal {H}_B$
.
Remark 3.4. Recently, [Reference Chevalier and Hrushovski4] develops some results of this kind outside the context of
![]() $\omega $
-categorical structures.
$\omega $
-categorical structures.
Note that the space of constant functions is closed in
![]() $L^2(\mu )$
; hence, from Proposition 2.2 we get:
$L^2(\mu )$
; hence, from Proposition 2.2 we get:
Corollary 3.5. Let
![]() $\mu $
be an ergodic measure on
$\mu $
be an ergodic measure on
![]() $\mathcal {M}^{eq}$
in the variable x. Then,
$\mathcal {M}^{eq}$
in the variable x. Then,
![]() $L^2(\mu )_{\mathrm {dcl}^{eq}(\emptyset )}$
is generated by the constant indicator function
$L^2(\mu )_{\mathrm {dcl}^{eq}(\emptyset )}$
is generated by the constant indicator function
![]() $\mathbb {1}$
.
$\mathbb {1}$
.
Proof Suppose
![]() $f\in L^2(\mu )_{\mathrm {dcl}^{eq}(\emptyset )}$
. Then, for some finite
$f\in L^2(\mu )_{\mathrm {dcl}^{eq}(\emptyset )}$
. Then, for some finite
![]() $C\subseteq \mathrm {dcl}^{eq}(\emptyset )$
, f is
$C\subseteq \mathrm {dcl}^{eq}(\emptyset )$
, f is
![]() $G_C$
-invariant. However, since any element in
$G_C$
-invariant. However, since any element in
![]() $\mathrm {dcl}^{eq}(\emptyset )$
is fixed by
$\mathrm {dcl}^{eq}(\emptyset )$
is fixed by
![]() $\mathrm {Aut}(M^{eq})$
-automorphisms,
$\mathrm {Aut}(M^{eq})$
-automorphisms,
![]() $G_C=G_\emptyset $
. This means that f is invariant almost everywhere, and therefore constant by ergodicity of the measure.
$G_C=G_\emptyset $
. This means that f is invariant almost everywhere, and therefore constant by ergodicity of the measure.
An ergodic measure also concentrates on an orbit. So, for ergodic
![]() $\mu $
, in
$\mu $
, in
![]() $L^2(\mu )$
the constant function
$L^2(\mu )$
the constant function
![]() $\mathbb {1}$
will be in the same equivalence class as
$\mathbb {1}$
will be in the same equivalence class as
![]() $\mathbb {1}_\phi $
, where
$\mathbb {1}_\phi $
, where
![]() $\phi $
isolates one of the finitely many types over the empty set, by Ryll-Nardzewski.
$\phi $
isolates one of the finitely many types over the empty set, by Ryll-Nardzewski.
Definition 3.6. Let
![]() $A, B, C \subseteq \mathcal {M}^{eq}$
. Then, A and C are weakly algebraically independent over B, written
$A, B, C \subseteq \mathcal {M}^{eq}$
. Then, A and C are weakly algebraically independent over B, written ![]() if
if
![]() $\mathrm {acl}^{eq}(AB)\cap \mathrm {acl}^{eq}(BC)=\mathrm {acl}^{eq}(B)$
.
$\mathrm {acl}^{eq}(AB)\cap \mathrm {acl}^{eq}(BC)=\mathrm {acl}^{eq}(B)$
.
Theorem 3.3 yields very powerful results when considering an ergodic measure and the inner product on
![]() $L^2(\mu )$
.
$L^2(\mu )$
.
Theorem 3.7. Let
![]() $\mathcal {M}$
be an
$\mathcal {M}$
be an
![]() $\omega $
-categorical countable structure with
$\omega $
-categorical countable structure with
![]() $\mathrm {acl}^{eq}(\emptyset )=\mathrm {dcl}^{eq}(\emptyset )$
. Consider the complex Hilbert space
$\mathrm {acl}^{eq}(\emptyset )=\mathrm {dcl}^{eq}(\emptyset )$
. Consider the complex Hilbert space
![]() $\mathcal {H}=L^2(\mu )$
, where
$\mathcal {H}=L^2(\mu )$
, where
![]() $\mu $
is an ergodic measure. Suppose that
$\mu $
is an ergodic measure. Suppose that
![]() $A, B \subseteq M^{eq}$
are algebraically closed and that
$A, B \subseteq M^{eq}$
are algebraically closed and that ![]() . Let
. Let
![]() $f\in \mathcal {H}_A, g\in \mathcal {H}_B$
. Then,
$f\in \mathcal {H}_A, g\in \mathcal {H}_B$
. Then,
Proof Let
![]() $f_0$
and
$f_0$
and
![]() $g_0$
be the projections of f and g, respectively, on
$g_0$
be the projections of f and g, respectively, on
![]() $\mathcal {H}_\emptyset $
. Now, since
$\mathcal {H}_\emptyset $
. Now, since
![]() $f\perp _{\mathcal {H}_\emptyset } g$
,
$f\perp _{\mathcal {H}_\emptyset } g$
,
![]() $\langle f, g \rangle =\langle f_0, g_0 \rangle $
. Since
$\langle f, g \rangle =\langle f_0, g_0 \rangle $
. Since
![]() $f_0, g_0\in \mathcal {H}_\emptyset $
, by Lemma 3.5,
$f_0, g_0\in \mathcal {H}_\emptyset $
, by Lemma 3.5,
![]() $f_0=\alpha \mathbb {1}$
,
$f_0=\alpha \mathbb {1}$
,
![]() $g=\beta \mathbb {1}$
for
$g=\beta \mathbb {1}$
for
![]() $\alpha , \beta \in \mathbb {C}$
. Now, this yields that
$\alpha , \beta \in \mathbb {C}$
. Now, this yields that
Being in a probability space,
![]() $\langle \mathbb {1}, \mathbb {1}\rangle =1$
. However, since
$\langle \mathbb {1}, \mathbb {1}\rangle =1$
. However, since
![]() $\langle f-f_0, f_0\rangle =0$
, we obtain that
$\langle f-f_0, f_0\rangle =0$
, we obtain that
![]() $\langle f, \mathbb {1} \rangle =\alpha $
, and similarly,
$\langle f, \mathbb {1} \rangle =\alpha $
, and similarly,
![]() $\langle g, \mathbb {1} \rangle =\beta $
. This yields the desired result.
$\langle g, \mathbb {1} \rangle =\beta $
. This yields the desired result.
This is already substantially observed in Corollary 3.5 and Remark 3.6 of [Reference Jahel and Tsankov13]. In particular, since we are interested in the measures of formulas, we have that:
Corollary 3.8. Let
![]() $\mathcal {M}$
be
$\mathcal {M}$
be
![]() $\omega $
-categorical. Let
$\omega $
-categorical. Let
![]() $\mu $
be an ergodic measure on
$\mu $
be an ergodic measure on
![]() ${M}^{eq}$
in the variable x. Suppose that
${M}^{eq}$
in the variable x. Suppose that
![]() $\mathrm {acl}^{eq}(\emptyset )=\mathrm {dcl}^{eq}(\emptyset )$
. Let
$\mathrm {acl}^{eq}(\emptyset )=\mathrm {dcl}^{eq}(\emptyset )$
. Let
![]() $a, {b}$
be tuples from
$a, {b}$
be tuples from
![]() $\mathcal {M}^{eq}$
such that
$\mathcal {M}^{eq}$
such that ![]() . Then, for any
. Then, for any
![]() $\mathcal {L}^{eq}$
-formulas
$\mathcal {L}^{eq}$
-formulas
![]() $\phi (x, {y}), \psi (x, {z})$
,
$\phi (x, {y}), \psi (x, {z})$
,
Proof Note that the indicator functions
![]() $\mathbb {1}_{\phi (x, {a})}$
and
$\mathbb {1}_{\phi (x, {a})}$
and
![]() $\mathbb {1}_{\psi (x, {b})}$
are in
$\mathbb {1}_{\psi (x, {b})}$
are in
![]() $\mathcal {H}_{\mathrm {acl}^{eq}({a})}$
and
$\mathcal {H}_{\mathrm {acl}^{eq}({a})}$
and
![]() $\mathcal {H}_{\mathrm {acl}^{eq}({b})}$
, respectively, and that
$\mathcal {H}_{\mathrm {acl}^{eq}({b})}$
, respectively, and that
 $$ \begin{align*} \mu(\phi(x, {a})\cap \psi(x, {b})) & = \int_{S_x(M)} \mathbb{1}_{\phi(x, {a})\cap\psi(x, {b})} \mathrm{d}\mu\\ & =\int_{S_x(M)} \mathbb{1}_{\phi(x, {a})}\cdot \mathbb{1}_{\psi(x, {b})} \mathrm{d}\mu \\ & = \left(\int_{S_x(M)} \mathbb{1}_{\phi(x, A)}\mathrm{d}\mu\right)\overline{\left(\int_{S_x(M)} \mathbb{1}_{\phi(x, {a})}\mathrm{d}\mu\right)} \\ &=\mu(\phi(x, {a}))\overline{\mu(\psi(x, {b}))} \\ &= \mu(\phi(x, {a}))\mu(\psi(x, {b})). \end{align*} $$
$$ \begin{align*} \mu(\phi(x, {a})\cap \psi(x, {b})) & = \int_{S_x(M)} \mathbb{1}_{\phi(x, {a})\cap\psi(x, {b})} \mathrm{d}\mu\\ & =\int_{S_x(M)} \mathbb{1}_{\phi(x, {a})}\cdot \mathbb{1}_{\psi(x, {b})} \mathrm{d}\mu \\ & = \left(\int_{S_x(M)} \mathbb{1}_{\phi(x, A)}\mathrm{d}\mu\right)\overline{\left(\int_{S_x(M)} \mathbb{1}_{\phi(x, {a})}\mathrm{d}\mu\right)} \\ &=\mu(\phi(x, {a}))\overline{\mu(\psi(x, {b}))} \\ &= \mu(\phi(x, {a}))\mu(\psi(x, {b})). \end{align*} $$
Here the third equality holds by Theorem 3.7 and the last one follows since our measure is real-valued. Hence, the result follows.
Remark 3.9. This corollary has a partial converse which is well known in ergodic theory [Reference Jahel and Tsankov13, Proposition 4.8]. Fix an invariant Keisler measure
![]() $\mu $
and suppose that for any formula
$\mu $
and suppose that for any formula
![]() $\phi (x,a)$
there is an automorphism
$\phi (x,a)$
there is an automorphism
![]() $\sigma \in \mathrm {Aut}(M)$
such that
$\sigma \in \mathrm {Aut}(M)$
such that
Then,
![]() $\mu $
is ergodic.
$\mu $
is ergodic.
We conclude this section with a brief discussion of the assumption of
![]() $\mathrm {acl}^{eq}(\emptyset )=\mathrm {dcl}^{eq}(\emptyset )$
in Theorem 3.7 and Corollary 3.8. The assumption is needed in order to have the equality
$\mathrm {acl}^{eq}(\emptyset )=\mathrm {dcl}^{eq}(\emptyset )$
in Theorem 3.7 and Corollary 3.8. The assumption is needed in order to have the equality
![]() $L^2(\mu )_{\mathrm {acl}^{eq}(\emptyset )}= L^2(\mu )_{\mathrm {dcl}^{eq}(\emptyset )}$
. The latter then yields the desired results since we know from Corollary 3.5 that
$L^2(\mu )_{\mathrm {acl}^{eq}(\emptyset )}= L^2(\mu )_{\mathrm {dcl}^{eq}(\emptyset )}$
. The latter then yields the desired results since we know from Corollary 3.5 that
![]() $L^2(\mu )_{\mathrm {dcl}^{eq}(\emptyset )}$
is generated by the constant indicator function. However, we can also obtain the relevant independence results when
$L^2(\mu )_{\mathrm {dcl}^{eq}(\emptyset )}$
is generated by the constant indicator function. However, we can also obtain the relevant independence results when
![]() $\mathrm {acl}^{eq}(\emptyset )\supsetneq \mathrm {dcl}^{eq}(\emptyset )$
. The following lemma is common knowledge:
$\mathrm {acl}^{eq}(\emptyset )\supsetneq \mathrm {dcl}^{eq}(\emptyset )$
. The following lemma is common knowledge:
Lemma 3.10. Let
![]() $\mathcal {M}$
be
$\mathcal {M}$
be
![]() $\omega $
-categorical. Let
$\omega $
-categorical. Let
![]() $A\subseteq M$
be finite. Fix the variable x in the home sort. Then, there is
$A\subseteq M$
be finite. Fix the variable x in the home sort. Then, there is
![]() $A_0\subseteq \mathrm {acl}^{eq}(A)$
finite such that for every b, a tuple from
$A_0\subseteq \mathrm {acl}^{eq}(A)$
finite such that for every b, a tuple from
![]() $\mathcal {M}$
in the variable x,
$\mathcal {M}$
in the variable x,
By this we mean that if b and
![]() $b'$
in the variable x have the same type over
$b'$
in the variable x have the same type over
![]() $A_0$
, then they have the same type over
$A_0$
, then they have the same type over
![]() $\mathrm {acl}^{eq}(A)$
in
$\mathrm {acl}^{eq}(A)$
in
![]() $\mathcal {M}^{eq}$
.
$\mathcal {M}^{eq}$
.
Proof This is substantially Lemma 2.4 in [Reference Evans and Tsankov9].
A useful consequences of the lemma is:
Corollary 3.11. Let
![]() $\mathcal {M}$
be
$\mathcal {M}$
be
![]() $\omega $
-categorical. Let
$\omega $
-categorical. Let
![]() $\mu $
be an invariant Keisler measure on
$\mu $
be an invariant Keisler measure on
![]() $\mathcal {M}^{eq}$
in the variable x. Then, there is finite
$\mathcal {M}^{eq}$
in the variable x. Then, there is finite
![]() $A_0\subseteq \mathrm {acl}^{eq}(\emptyset )$
such that
$A_0\subseteq \mathrm {acl}^{eq}(\emptyset )$
such that
Proof Let
![]() $A_0\subseteq \mathrm {acl}^{eq}(\emptyset )$
be finite such that 3.1 from Lemma 3.10 holds. Suppose that
$A_0\subseteq \mathrm {acl}^{eq}(\emptyset )$
be finite such that 3.1 from Lemma 3.10 holds. Suppose that
![]() $f\in L^2(\mu )$
is
$f\in L^2(\mu )$
is
![]() $G_A$
-invariant for
$G_A$
-invariant for
![]() $G=\mathrm {Aut}(M^{eq})$
and A a finite subset of
$G=\mathrm {Aut}(M^{eq})$
and A a finite subset of
![]() $\mathrm {acl}^{eq}(\emptyset )$
. Then, f is also
$\mathrm {acl}^{eq}(\emptyset )$
. Then, f is also
![]() $G_{A'}$
-invariant for
$G_{A'}$
-invariant for
![]() $A'=A\cup A_0$
. But then, by choice of
$A'=A\cup A_0$
. But then, by choice of
![]() $A_0$
(with respect to the variable x), the
$A_0$
(with respect to the variable x), the
![]() $G_{A'}$
-orbit of any type in
$G_{A'}$
-orbit of any type in
![]() $S_x(M^{eq})$
is the same as its
$S_x(M^{eq})$
is the same as its
![]() $G_{A_0}$
-orbit. Hence, f is
$G_{A_0}$
-orbit. Hence, f is
![]() $G_{A_0}$
-invariant.
$G_{A_0}$
-invariant.
For an
![]() $\omega $
-categorical structure
$\omega $
-categorical structure
![]() $\mathcal {M}$
and given the variable x and
$\mathcal {M}$
and given the variable x and
![]() $A_0$
as above, there are finitely many types over
$A_0$
as above, there are finitely many types over
![]() $A_0$
in the variable x, isolated by formulas
$A_0$
in the variable x, isolated by formulas
![]() $\chi _1(x), \dots , \chi _m(x)$
. By additivity, any invariant Keisler measure
$\chi _1(x), \dots , \chi _m(x)$
. By additivity, any invariant Keisler measure
![]() $\mu $
can be written as a weighted sum of measures
$\mu $
can be written as a weighted sum of measures
![]() $\mu _{\chi _i}$
for
$\mu _{\chi _i}$
for
![]() $1\leq i\leq m'\leq m$
, where, for
$1\leq i\leq m'\leq m$
, where, for
![]() $\mu (\chi _i(x))>0$
,
$\mu (\chi _i(x))>0$
,
![]() $\mu _{\chi _i}$
is the
$\mu _{\chi _i}$
is the
![]() $\mathrm {Aut}(M/A_0)$
-invariant Keisler measure induced from
$\mathrm {Aut}(M/A_0)$
-invariant Keisler measure induced from
![]() $\mu $
by
$\mu $
by
 $$\begin{align*}\mu_{\chi_i}(\phi(x,a))=\frac{\mu(\phi(x,a)\wedge \chi_i(x))}{\mu(\chi_i(x))}.\end{align*}$$
$$\begin{align*}\mu_{\chi_i}(\phi(x,a))=\frac{\mu(\phi(x,a)\wedge \chi_i(x))}{\mu(\chi_i(x))}.\end{align*}$$
From Corollary 3.11, we know that for any
![]() $\mathrm {Aut}(M/A_0)$
-ergodic measure
$\mathrm {Aut}(M/A_0)$
-ergodic measure
![]() $\nu $
we have that for
$\nu $
we have that for ![]() , and
, and
![]() $\mathcal {L}^{eq}$
-formulas
$\mathcal {L}^{eq}$
-formulas
![]() $\phi (x,y), \psi (x, z)$
,
$\phi (x,y), \psi (x, z)$
,
Hence, in the context of
![]() $\mathrm {acl}^{eq}(\emptyset )\supsetneq \mathrm {dcl}^{eq}(\emptyset )$
, in order to study invariant Keisler measures on an
$\mathrm {acl}^{eq}(\emptyset )\supsetneq \mathrm {dcl}^{eq}(\emptyset )$
, in order to study invariant Keisler measures on an
![]() $\omega $
-categorical structure
$\omega $
-categorical structure
![]() $\mathcal {M}$
we may naturally move to study the
$\mathcal {M}$
we may naturally move to study the
![]() $\mathrm {Aut}(M/A_0)$
-invariant Keisler measures.
$\mathrm {Aut}(M/A_0)$
-invariant Keisler measures.
4. A strong independence theorem
In this section, we prove that in a simple
![]() $\omega $
-categorical structure
$\omega $
-categorical structure
![]() $\mathcal {M}$
with
$\mathcal {M}$
with
![]() $\mathrm {acl}^{eq}(\emptyset )=\mathrm {dcl}^{eq}(\emptyset )$
if forking over the empty set is the same as being universally measure zero, then
$\mathrm {acl}^{eq}(\emptyset )=\mathrm {dcl}^{eq}(\emptyset )$
if forking over the empty set is the same as being universally measure zero, then
![]() $\mathcal {M}$
satisfies a stronger version of the independence theorem over finite algebraically closed sets. We conclude with some consequences for
$\mathcal {M}$
satisfies a stronger version of the independence theorem over finite algebraically closed sets. We conclude with some consequences for
![]() $\omega $
-categorical
$\omega $
-categorical
![]() $MS$
-measurable structures. Unless specified otherwise,
$MS$
-measurable structures. Unless specified otherwise,
![]() $\mathcal {M}$
denotes the countable model of an
$\mathcal {M}$
denotes the countable model of an
![]() $\omega $
-categorical theory.
$\omega $
-categorical theory.
Firstly, we note how the measure
![]() $\mu (\phi (x, a)\wedge \psi (x, b))$
only depends on the types of the individual parameters when a and b are weakly algebraically independent.
$\mu (\phi (x, a)\wedge \psi (x, b))$
only depends on the types of the individual parameters when a and b are weakly algebraically independent.
Corollary 4.1. Let
![]() $\mathcal {M}$
be an
$\mathcal {M}$
be an
![]() $\omega $
-categorical structure with
$\omega $
-categorical structure with
![]() $\mathrm {acl}^{eq}(\emptyset )=\mathrm {dcl}^{eq}(\emptyset )$
. Suppose that
$\mathrm {acl}^{eq}(\emptyset )=\mathrm {dcl}^{eq}(\emptyset )$
. Suppose that
![]() $a, b\in \mathcal {M}^{eq}$
are such that
$a, b\in \mathcal {M}^{eq}$
are such that ![]() . Let
. Let
![]() $\phi (x, y), \psi (x, z)$
be
$\phi (x, y), \psi (x, z)$
be
![]() $\mathcal {L}^{eq}$
-formulas. Then, for an arbitrary
$\mathcal {L}^{eq}$
-formulas. Then, for an arbitrary
![]() $\mathrm {Aut}(M)$
-invariant Keisler measure
$\mathrm {Aut}(M)$
-invariant Keisler measure
![]() $\mu : \mathrm {Def}_x(M)\to [0,1]$
,
$\mu : \mathrm {Def}_x(M)\to [0,1]$
,
only depends on
![]() $\mathrm {tp}(a)$
and
$\mathrm {tp}(a)$
and
![]() $\mathrm {tp}(b)$
.
$\mathrm {tp}(b)$
.
Proof Let ![]() be such that
be such that
![]() $a'\equiv a$
and
$a'\equiv a$
and
![]() $b'\equiv b$
. Then, by Corollary 3.8, we get that for any ergodic measure
$b'\equiv b$
. Then, by Corollary 3.8, we get that for any ergodic measure
![]() $\nu $
,
$\nu $
,
But then, by the ergodic decomposition, Corollary 2.8, we have that for any
![]() $\mathrm {Aut}(M)$
-invariant Keisler measure
$\mathrm {Aut}(M)$
-invariant Keisler measure
Definition 4.2. Let
![]() $\mathcal {M}$
be an
$\mathcal {M}$
be an
![]() $\mathcal {L}$
-structure and
$\mathcal {L}$
-structure and
![]() $A\subset M$
. We write
$A\subset M$
. We write
![]() $F(A)$
for the set of formulas with parameters from
$F(A)$
for the set of formulas with parameters from
![]() $\mathcal {M}$
forking over A.
$\mathcal {M}$
forking over A.
Following Remark 2.6, we always compare the forking and universally measure zero ideals in sufficiently saturated and strongly homogeneous models. As noted in the introduction, from [Reference Chernikov, Hrushovski, Kruckman, Krupiński, Moconja, Pillay and Ramsey3] we know that
![]() $F(\emptyset )\subseteq \mathcal {O}(\emptyset )$
. We are interested in studying what happens when
$F(\emptyset )\subseteq \mathcal {O}(\emptyset )$
. We are interested in studying what happens when
![]() $F(\emptyset )=\mathcal {O}(\emptyset )$
in order to find a structure where the two sets differ.
$F(\emptyset )=\mathcal {O}(\emptyset )$
in order to find a structure where the two sets differ.
Definition 4.3. Let
![]() $\mathcal {M}$
be an
$\mathcal {M}$
be an
![]() $\mathcal {L}$
-structure. We say that
$\mathcal {L}$
-structure. We say that
![]() $\mathcal {M}$
satisfies the strong independence theorem over
$\mathcal {M}$
satisfies the strong independence theorem over
![]() $A\subseteq \mathcal {M}^{eq}$
if the following holds:
$A\subseteq \mathcal {M}^{eq}$
if the following holds:
Let
![]() $a, b, c_0, c_1\in M^{eq}$
be such that
$a, b, c_0, c_1\in M^{eq}$
be such that ![]() ,
,
![]() $c_0\equiv _A c_1$
and
$c_0\equiv _A c_1$
and ![]() ,
, ![]() . Then, there is
. Then, there is
![]() $c^*\in \mathcal {M}^{eq}$
such that
$c^*\in \mathcal {M}^{eq}$
such that
![]() $c^*\equiv _{Aa} c_0, c^*\equiv _{Ab} c_1$
, and
$c^*\equiv _{Aa} c_0, c^*\equiv _{Ab} c_1$
, and ![]() .
.
Here, the relation ![]() denotes non-forking independence. From Corollary 4.1 we obtain that simple
denotes non-forking independence. From Corollary 4.1 we obtain that simple
![]() $\omega $
-categorical structures where forking coincides with being universally measure zero satisfy the strong independence theorem over the empty set.
$\omega $
-categorical structures where forking coincides with being universally measure zero satisfy the strong independence theorem over the empty set.
Theorem 4.4. Let
![]() $\mathcal {M}$
be a simple
$\mathcal {M}$
be a simple
![]() $\omega $
-categorical structure with
$\omega $
-categorical structure with
![]() $\mathrm {acl}^{eq}(\emptyset )=\mathrm {dcl}^{eq}(\emptyset )$
. Suppose that
$\mathrm {acl}^{eq}(\emptyset )=\mathrm {dcl}^{eq}(\emptyset )$
. Suppose that
![]() $F(\emptyset )=\mathcal {O}(\emptyset )$
, i.e., a formula forks over the empty set if and only if it is universally measure zero. Then,
$F(\emptyset )=\mathcal {O}(\emptyset )$
, i.e., a formula forks over the empty set if and only if it is universally measure zero. Then,
![]() $\mathcal {M}$
satisfies the strong independence theorem over the empty set.
$\mathcal {M}$
satisfies the strong independence theorem over the empty set.
Proof Suppose that there are
![]() $a, b, c_0, c_1\in \mathcal {M}^{eq}$
as in Definition 4.3. Let
$a, b, c_0, c_1\in \mathcal {M}^{eq}$
as in Definition 4.3. Let
![]() $\phi (x, a)$
and
$\phi (x, a)$
and
![]() $\psi (x, b)$
isolate
$\psi (x, b)$
isolate
![]() $\mathrm {tp}(c_0/a)$
and
$\mathrm {tp}(c_0/a)$
and
![]() $\mathrm {tp}(c_1/b)$
. By the existence property of non-forking independence, there is
$\mathrm {tp}(c_1/b)$
. By the existence property of non-forking independence, there is
![]() $b'\equiv b$
such that
$b'\equiv b$
such that ![]() . By Corollary 4.1, for any Keisler measure,
. By Corollary 4.1, for any Keisler measure,
By simplicity,
![]() $\phi (x, a)\wedge \psi (x, b')$
does not fork over the empty set since the independence theorem holds over
$\phi (x, a)\wedge \psi (x, b')$
does not fork over the empty set since the independence theorem holds over
![]() $\emptyset $
. Hence, by
$\emptyset $
. Hence, by
![]() $F(\emptyset )=\mathcal {O}(\emptyset )$
,
$F(\emptyset )=\mathcal {O}(\emptyset )$
,
![]() $\phi (x, a)\wedge \psi (x, b)$
is not universally measure zero, and so is non-forking over the empty set. This proves the strong independence theorem over the empty set for
$\phi (x, a)\wedge \psi (x, b)$
is not universally measure zero, and so is non-forking over the empty set. This proves the strong independence theorem over the empty set for
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Remark 4.5. In general, a simple
![]() $\omega $
-categorical theory with
$\omega $
-categorical theory with
![]() $\mathrm {acl}^{eq}(\emptyset )=\mathrm {dcl}^{eq}(\emptyset )$
satisfies the independence theorem over the empty set (see, for example, [Reference Marimon17]). However, the condition of
$\mathrm {acl}^{eq}(\emptyset )=\mathrm {dcl}^{eq}(\emptyset )$
satisfies the independence theorem over the empty set (see, for example, [Reference Marimon17]). However, the condition of
![]() $F(\emptyset )=\mathcal {O}(\emptyset )$
yields a strengthening of the independence theorem, where the “base” of the amalgamation is weakly algebraically independent rather than non-forking independent. In fact, while non-forking independence implies weak algebraic independence, the converse does not hold in general.
$F(\emptyset )=\mathcal {O}(\emptyset )$
yields a strengthening of the independence theorem, where the “base” of the amalgamation is weakly algebraically independent rather than non-forking independent. In fact, while non-forking independence implies weak algebraic independence, the converse does not hold in general.
Definition 4.6. We say that an
![]() $\omega $
-categorical simple structure
$\omega $
-categorical simple structure
![]() $\mathcal {M}$
is one-based if given
$\mathcal {M}$
is one-based if given
![]() $A, B\subseteq \mathcal {M}^{eq}$
algebraically closed, then
$A, B\subseteq \mathcal {M}^{eq}$
algebraically closed, then
If
![]() $\mathcal {M}$
is one-based, for
$\mathcal {M}$
is one-based, for
![]() $A\subseteq M$
we have that
$A\subseteq M$
we have that
In particular, in a one-based structure, satisfying the independence theorem over A is equivalent to satisfying the strong independence theorem over A.
However, there are not one-based simple
![]() $\omega $
-categorical structures. The only known example of this are
$\omega $
-categorical structures. The only known example of this are
![]() $\omega $
-categorical Hrushovski constructions. For these, to satisfy the strong independence theorem is a genuinely stronger requirement than satisfying the independence theorem.
$\omega $
-categorical Hrushovski constructions. For these, to satisfy the strong independence theorem is a genuinely stronger requirement than satisfying the independence theorem.
We conclude this section with some consequences for
![]() $MS$
-measurable structures in an
$MS$
-measurable structures in an
![]() $\omega $
-categorical context. For a general introduction to
$\omega $
-categorical context. For a general introduction to
![]() $MS$
-measurable structures we suggest [Reference Elwes, Macpherson, Chatzidakis, Macpherson, Pillay and Wilkie7] or the original article [Reference Macpherson and Steinhorn16]. In [Reference Marimon17], I discuss in detail
$MS$
-measurable structures we suggest [Reference Elwes, Macpherson, Chatzidakis, Macpherson, Pillay and Wilkie7] or the original article [Reference Macpherson and Steinhorn16]. In [Reference Marimon17], I discuss in detail
![]() $\omega $
-categorical
$\omega $
-categorical
![]() $MS$
-measurable structures, and we direct the reader to that article for the relevant definitions and some basic results. The general idea is that
$MS$
-measurable structures, and we direct the reader to that article for the relevant definitions and some basic results. The general idea is that
![]() $MS$
-measurable structures have an associated dimension-measure function assigning each definable set a dimension and a measure. The dimension-measure function is invariant (and definable), the measure always takes strictly positive values, and the dimension and the measure satisfy Fubini’s theorem. Being
$MS$
-measurable structures have an associated dimension-measure function assigning each definable set a dimension and a measure. The dimension-measure function is invariant (and definable), the measure always takes strictly positive values, and the dimension and the measure satisfy Fubini’s theorem. Being
![]() $MS$
-measurable is a property of a theory. An important feature proved in [Reference Macpherson and Steinhorn16] is that
$MS$
-measurable is a property of a theory. An important feature proved in [Reference Macpherson and Steinhorn16] is that
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $MS$
-measurable if and only if
$MS$
-measurable if and only if
![]() $\mathcal {M}^{eq}$
is.
$\mathcal {M}^{eq}$
is.
Remark 4.7. The dimension d of the dimension-measure function in an
![]() $MS$
-measurable theory induces a natural notion of independence: for tuples
$MS$
-measurable theory induces a natural notion of independence: for tuples
![]() $b,c$
, and small A, we write
$b,c$
, and small A, we write
where for a tuple b and A small,
A folklore result attributed to Ben-Yaacov in [Reference Elwes, Macpherson, Chatzidakis, Macpherson, Pillay and Wilkie7] is that this notion of independence corresponds to non-forking independence. See [Reference Marimon17] for a proof of this. Using this fact, we can prove that in
![]() $MS$
-measurable theories forking coincides with being universally measure zero (over any small set).
$MS$
-measurable theories forking coincides with being universally measure zero (over any small set).
Lemma 4.8. Let
![]() $\mathbb {M}$
be the monster model of an
$\mathbb {M}$
be the monster model of an
![]() $MS$
-measurable theory. Then,
$MS$
-measurable theory. Then,
![]() $F(A)=\mathcal {O}(A)$
for any small
$F(A)=\mathcal {O}(A)$
for any small
![]() $A\subseteq \mathbb {M}$
.
$A\subseteq \mathbb {M}$
.
Proof Suppose there is a formula
![]() $\phi (x,b)$
which does not fork over A, but has measure zero for every
$\phi (x,b)$
which does not fork over A, but has measure zero for every
![]() $\mathrm {Aut}(\mathbb {M}/A)$
-invariant Keisler measure. Let
$\mathrm {Aut}(\mathbb {M}/A)$
-invariant Keisler measure. Let
![]() $c\vDash \phi (x,b)$
be such that
$c\vDash \phi (x,b)$
be such that ![]() . Since dimension-independence corresponds to non-forking independence, as noted in Remark 4.7,
. Since dimension-independence corresponds to non-forking independence, as noted in Remark 4.7,
![]() $d(c/Ab)=d(c/A)$
. Let
$d(c/Ab)=d(c/A)$
. Let
![]() $\psi (x,a)\in \mathrm {tp}(c/A)$
be such that
$\psi (x,a)\in \mathrm {tp}(c/A)$
be such that
![]() $d(\psi (x,a))=d(c/A)$
. By
$d(\psi (x,a))=d(c/A)$
. By
![]() $MS$
-measurability [Reference Macpherson and Steinhorn16, Proposition 5.3], we have an induced
$MS$
-measurability [Reference Macpherson and Steinhorn16, Proposition 5.3], we have an induced
![]() $\mathrm {Aut}(\mathbb {M}/A)$
-invariant Keisler measure
$\mathrm {Aut}(\mathbb {M}/A)$
-invariant Keisler measure
![]() $\mu _\psi $
on
$\mu _\psi $
on
![]() $\mathrm {Def}_x(\mathbb {M})$
given by
$\mathrm {Def}_x(\mathbb {M})$
given by
 $$\begin{align*}\mu_\psi(\chi(x,d))= \begin{cases} \frac{\mu(\chi(x,d)\wedge \psi(x,a))}{\mu(\psi(x,a))}, & \text{ for } d(\chi(x,d)\wedge \psi(x,a)))=d(\psi(x,a)),\\ 0, & \text{otherwise}, \end{cases} \end{align*}$$
$$\begin{align*}\mu_\psi(\chi(x,d))= \begin{cases} \frac{\mu(\chi(x,d)\wedge \psi(x,a))}{\mu(\psi(x,a))}, & \text{ for } d(\chi(x,d)\wedge \psi(x,a)))=d(\psi(x,a)),\\ 0, & \text{otherwise}, \end{cases} \end{align*}$$
where
![]() $\mu $
is the measure in the dimension-measure. Being universally measure zero (over A), we have that
$\mu $
is the measure in the dimension-measure. Being universally measure zero (over A), we have that
![]() $\mu _\psi (\phi (x,b))=\mu (\phi (x,b)\wedge \psi (x,a))=0$
, which contradicts positivity of the measure.
$\mu _\psi (\phi (x,b))=\mu (\phi (x,b)\wedge \psi (x,a))=0$
, which contradicts positivity of the measure.
From Corollary 4.1 we obtain that
![]() $\omega $
-categorical
$\omega $
-categorical
![]() $MS$
-measurable structures satisfy the strong independence theorem over the algebraic closures of finite sets. Indeed, we also get the corresponding probabilistic independence statement. Recall from Lemma 3.10 that for
$MS$
-measurable structures satisfy the strong independence theorem over the algebraic closures of finite sets. Indeed, we also get the corresponding probabilistic independence statement. Recall from Lemma 3.10 that for
![]() $A\subseteq M^{eq}$
the algebraic closure of a finite set, and fixing the variable x, there is
$A\subseteq M^{eq}$
the algebraic closure of a finite set, and fixing the variable x, there is
![]() $A_0\subset A$
finite such that types in the variable x over A are isolated by
$A_0\subset A$
finite such that types in the variable x over A are isolated by
![]() $\mathcal {L}^{eq}$
-formulas with parameters from
$\mathcal {L}^{eq}$
-formulas with parameters from
![]() $A_0$
.
$A_0$
.
Theorem 4.9. Let
![]() $\mathcal {M}$
be
$\mathcal {M}$
be
![]() $\omega $
-categorical and
$\omega $
-categorical and
![]() $MS$
-measurable. Then, it satisfies the strong independence theorem over the algebraic closures of finite sets:
$MS$
-measurable. Then, it satisfies the strong independence theorem over the algebraic closures of finite sets:
Let
![]() $A\subseteq M^{eq}$
be the algebraic closure of a finite set,
$A\subseteq M^{eq}$
be the algebraic closure of a finite set,
![]() $a_0, a_1, b, c$
tuples from
$a_0, a_1, b, c$
tuples from
![]() $M^{eq}$
. Suppose
$M^{eq}$
. Suppose
![]() $a_0\equiv _A a_1$
,
$a_0\equiv _A a_1$
, ![]() , and that
, and that ![]() ,
, ![]() . Then, there is
. Then, there is
![]() $a^*$
such that
$a^*$
such that
![]() $a^*\equiv _{Ab} a_0$
,
$a^*\equiv _{Ab} a_0$
,
![]() $a^*\equiv _{Ac} a_1$
, and
$a^*\equiv _{Ac} a_1$
, and ![]() . Moreover,
. Moreover,
 $$\begin{align*}\mu(\mathrm{tp}(a_0/Ab)\cup \mathrm{tp}(a_1/Ac))=\frac{\mu(a_0/Ab)\mu(a_1/Ac)}{\mu(a_0/A)}.\end{align*}$$
$$\begin{align*}\mu(\mathrm{tp}(a_0/Ab)\cup \mathrm{tp}(a_1/Ac))=\frac{\mu(a_0/Ab)\mu(a_1/Ac)}{\mu(a_0/A)}.\end{align*}$$
Proof In [Reference Marimon17] we proved a version of this statement where ![]() (instead of
(instead of ![]() ) simplifying some more general results in [Reference Hrushovski11]. We shall use this and Corollary 4.1 to deduce the theorem. Let
) simplifying some more general results in [Reference Hrushovski11]. We shall use this and Corollary 4.1 to deduce the theorem. Let
![]() $\phi (x, b)$
and
$\phi (x, b)$
and
![]() $\psi (x, c)$
isolate
$\psi (x, c)$
isolate
![]() $\mathrm {tp}(a_0/Ab)$
and
$\mathrm {tp}(a_0/Ab)$
and
![]() $\mathrm {tp}(a_1/Ac)$
respectively. Let
$\mathrm {tp}(a_1/Ac)$
respectively. Let
![]() $\chi (x)$
isolate
$\chi (x)$
isolate
![]() $\mathrm {tp}(a_i/A)$
, and let
$\mathrm {tp}(a_i/A)$
, and let
![]() $\mu _\chi $
be the
$\mu _\chi $
be the
![]() $\mathrm {Aut}(M^{eq}/A)$
invariant Keisler measure induced by
$\mathrm {Aut}(M^{eq}/A)$
invariant Keisler measure induced by
![]() $\chi (x)$
. We consider
$\chi (x)$
. We consider
![]() $\mu _\chi (\phi (x, b)\wedge \psi (x, c))$
. By extension we can find
$\mu _\chi (\phi (x, b)\wedge \psi (x, c))$
. By extension we can find
![]() $c'\equiv _A c$
such that
$c'\equiv _A c$
such that ![]() . Since non-forking independence implies weak algebraic independence, by Corollary 4.1
. Since non-forking independence implies weak algebraic independence, by Corollary 4.1
But the former has positive measure by the independence theorem over algebraically closed sets (and d-independence being the same as non-forking independence). Hence,
![]() $\phi (x, b)\wedge \psi (x, c)$
must have a realisation which is independent from
$\phi (x, b)\wedge \psi (x, c)$
must have a realisation which is independent from
![]() $bc$
over A. From [Reference Marimon17], for
$bc$
over A. From [Reference Marimon17], for ![]() we have that
we have that
 $$\begin{align*}\mu(\phi(x, b)\wedge \psi(x, c'))=\frac{\mu(\phi(x, b))\mu(\psi(x, c))}{\mu(\chi(x))}.\end{align*}$$
$$\begin{align*}\mu(\phi(x, b)\wedge \psi(x, c'))=\frac{\mu(\phi(x, b))\mu(\psi(x, c))}{\mu(\chi(x))}.\end{align*}$$
However, multiplying both sides of (4.1) by
![]() $\mu (\chi (x))$
,
$\mu (\chi (x))$
,
This yields the desired equation.
Remark 4.10. By the proof above and Remark 3.9, an
![]() $MS$
-measurable
$MS$
-measurable
![]() $\omega $
-categorical structure induces various ergodic Keisler measures. Let
$\omega $
-categorical structure induces various ergodic Keisler measures. Let
![]() $A\subseteq M^{eq}$
be the algebraic closure of a finite set and
$A\subseteq M^{eq}$
be the algebraic closure of a finite set and
![]() $\chi (x)$
isolate a type over A. Then, the induced
$\chi (x)$
isolate a type over A. Then, the induced
![]() $\mathrm {Aut}(M/A)$
-invariant Keisler measure
$\mathrm {Aut}(M/A)$
-invariant Keisler measure
![]() $\mu _\chi $
is
$\mu _\chi $
is
![]() $\mathrm {Aut}(M/A)$
-ergodic. We can also prove this using [Reference Marimon17] and Remark 3.9.
$\mathrm {Aut}(M/A)$
-ergodic. We can also prove this using [Reference Marimon17] and Remark 3.9.
5. The counterexample
We are now ready to introduce our example of a simple
![]() $\omega $
-categorical structure with
$\omega $
-categorical structure with
![]() $F(\emptyset )\subsetneq \mathcal {O}(\emptyset )$
. It will be an
$F(\emptyset )\subsetneq \mathcal {O}(\emptyset )$
. It will be an
![]() $\omega $
-categorical Hrushovski construction. For details on Hrushovski constructions the reader may refer to [Reference Wagner, Kaye and Macpherson24, Section 6.2.1]. This construction is also used in [Reference Marimon17] as an example of an
$\omega $
-categorical Hrushovski construction. For details on Hrushovski constructions the reader may refer to [Reference Wagner, Kaye and Macpherson24, Section 6.2.1]. This construction is also used in [Reference Marimon17] as an example of an
![]() $\omega $
-categorical supersimple structure which is not
$\omega $
-categorical supersimple structure which is not
![]() $MS$
-measurable, so the reader may refer to that article for details on this particular construction. The basic idea is that (non-trivial) simple
$MS$
-measurable, so the reader may refer to that article for details on this particular construction. The basic idea is that (non-trivial) simple
![]() $\omega $
-categorical Hrushovski constructions are not one-based. Hence, there are pairs which are weakly algebraic independent, but forking-dependent. This allows us to build Hrushovski constructions which are simple but which do not satisfy the strong independence theorem.
$\omega $
-categorical Hrushovski constructions are not one-based. Hence, there are pairs which are weakly algebraic independent, but forking-dependent. This allows us to build Hrushovski constructions which are simple but which do not satisfy the strong independence theorem.
Theorem 5.1. There is an
![]() $\omega $
-categorical graph
$\omega $
-categorical graph
![]() $\mathcal {M}$
supersimple of
$\mathcal {M}$
supersimple of
![]() $SU$
-rank
$SU$
-rank
![]() $2$
with the following properties:
$2$
with the following properties:
-
•
 $\mathrm {Aut}(M)$
acts transitively on the vertices of M.
$\mathrm {Aut}(M)$
acts transitively on the vertices of M. -
• Points are algebraically closed.
-
• Edges are algebraically closed, but for
 $b\in M$
the formula
$b\in M$
the formula
 $E(x,b)$
asserting that x has an edge with b forks over
$E(x,b)$
asserting that x has an edge with b forks over
 $\emptyset $
.
$\emptyset $
. -
• For
 $a, b\in M$
with no edge between them,
$a, b\in M$
with no edge between them,
 $\mathrm {acl}(ab)=ab$
or
$\mathrm {acl}(ab)=ab$
or
 $\mathrm {acl}(ab)=abc$
, where
$\mathrm {acl}(ab)=abc$
, where
 $abc$
is a path of length two with endpoints a and b. In either case,
$abc$
is a path of length two with endpoints a and b. In either case,  .
. -
• The smallest k-cycle in
 $\mathcal {M}$
is a
$\mathcal {M}$
is a
 $6$
-cycle.
$6$
-cycle. -
• The structure
 $\mathcal {M}$
has weak elimination of imaginaries.
$\mathcal {M}$
has weak elimination of imaginaries.
Furthermore, we can choose
![]() $\mathcal {M}$
to satisfy independent n-amalgamation over the algebraic closures of finite sets for any
$\mathcal {M}$
to satisfy independent n-amalgamation over the algebraic closures of finite sets for any
![]() $n\in \mathbb {N}$
, and also for all
$n\in \mathbb {N}$
, and also for all
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Proof The structure is an
![]() $\omega $
-categorical Hrushovski construction. It is the same construction as in [Reference Marimon17, Construction 5.1]. In the appendix of that article we prove supersimplicity, weak elimination of imaginaries, and note how higher independent amalgamation can be obtained. The other properties also follow by construction and basic calculations with the dimension, recalling that in a Hrushovski construction, the Hrushovski dimension corresponds to
$\omega $
-categorical Hrushovski construction. It is the same construction as in [Reference Marimon17, Construction 5.1]. In the appendix of that article we prove supersimplicity, weak elimination of imaginaries, and note how higher independent amalgamation can be obtained. The other properties also follow by construction and basic calculations with the dimension, recalling that in a Hrushovski construction, the Hrushovski dimension corresponds to
![]() $SU$
-rank [Reference Wagner, Kaye and Macpherson24, Corollary 6.2.26].
$SU$
-rank [Reference Wagner, Kaye and Macpherson24, Corollary 6.2.26].
Remark 5.2. The graph
![]() $\mathcal {M}$
in Theorem 5.1 is also extremely amenable in the sense of [Reference Hrushovski, Krupiński and Pillay12]. That is, every type in
$\mathcal {M}$
in Theorem 5.1 is also extremely amenable in the sense of [Reference Hrushovski, Krupiński and Pillay12]. That is, every type in
![]() $S(\emptyset )$
extends to an
$S(\emptyset )$
extends to an
![]() $\mathrm {Aut}(M)$
-invariant type over M. Since invariant types can be considered as invariant Keisler measures taking only the values
$\mathrm {Aut}(M)$
-invariant type over M. Since invariant types can be considered as invariant Keisler measures taking only the values
![]() $0$
and
$0$
and
![]() $1$
, this guarantees that there are some invariant Keisler measures on
$1$
, this guarantees that there are some invariant Keisler measures on
![]() $\mathcal {M}$
in each variable. To see that these structures are extremely amenable, for a finite tuple
$\mathcal {M}$
in each variable. To see that these structures are extremely amenable, for a finite tuple
![]() $\overline {a}$
from M, consider the type
$\overline {a}$
from M, consider the type
![]() $p(\overline {x})$
given by
$p(\overline {x})$
given by
Substantially,
![]() $p(\overline {x})$
asserts that
$p(\overline {x})$
asserts that
![]() $\overline {x}$
has no relation to
$\overline {x}$
has no relation to
![]() $\mathcal {M}$
and is weakly algebraically independent from it. From [Reference Marimon17, Section 4] we can conclude that this type is consistent, complete, and invariant by the extension property and because types of finite tuples are determined by the quantifier-free types of their algebraic closures.
$\mathcal {M}$
and is weakly algebraically independent from it. From [Reference Marimon17, Section 4] we can conclude that this type is consistent, complete, and invariant by the extension property and because types of finite tuples are determined by the quantifier-free types of their algebraic closures.
It is commonly known that in a structure with weak elimination of imaginaries, for
![]() $A, B\subseteq M$
algebraically closed in
$A, B\subseteq M$
algebraically closed in
![]() $\mathcal {M}$
, we have that
$\mathcal {M}$
, we have that
Hence, for a and b sharing an edge, ![]() , but
, but
![]() $\mathrm {tp}(a/b)$
forks over
$\mathrm {tp}(a/b)$
forks over
![]() $\emptyset $
. Meanwhile, for a and c at distance two from each other,
$\emptyset $
. Meanwhile, for a and c at distance two from each other, ![]() . Hence, for
. Hence, for
![]() $\mathcal {M}$
to satisfy the strong independence theorem over the empty set,
$\mathcal {M}$
to satisfy the strong independence theorem over the empty set,
![]() $\mathcal {M}_f$
should include
$\mathcal {M}_f$
should include
![]() $5$
-cycles. But we have built
$5$
-cycles. But we have built
![]() $\mathcal {M}_f$
to exclude these. This implies the existence of a formula which does not fork over the empty set, but is universally measure zero. We can give this formula explicitly:
$\mathcal {M}_f$
to exclude these. This implies the existence of a formula which does not fork over the empty set, but is universally measure zero. We can give this formula explicitly:
Theorem 5.3. Let
![]() $\mathcal {M}$
be the
$\mathcal {M}$
be the
![]() $\omega $
-categorical structure described in Theorem 5.1. Let
$\omega $
-categorical structure described in Theorem 5.1. Let
![]() $\phi (x, y)$
be the formula stating that the points x and y are exactly at distance two from each other. Then, for
$\phi (x, y)$
be the formula stating that the points x and y are exactly at distance two from each other. Then, for
![]() $a\in M$
, the formula
$a\in M$
, the formula
![]() $\phi (x, a)$
is universally measure zero but does not fork over the empty set.
$\phi (x, a)$
is universally measure zero but does not fork over the empty set.
Proof Let
![]() $a, b\in M$
share an edge. Now,
$a, b\in M$
share an edge. Now,
![]() $\phi (x, a)\wedge \phi (x, b)$
is inconsistent since
$\phi (x, a)\wedge \phi (x, b)$
is inconsistent since
![]() $\mathcal {M}$
avoids
$\mathcal {M}$
avoids
![]() $5$
-cycles. Meanwhile,
$5$
-cycles. Meanwhile,
![]() $\phi (x, a)$
does not fork over the empty set since
$\phi (x, a)$
does not fork over the empty set since ![]() for c at distance two from a. However, since
for c at distance two from a. However, since ![]() , for an ergodic measure,
, for an ergodic measure,
where the second equality follows by Corollary 3.8 and the last equality by transitivity of the action of
![]() $\mathrm {Aut}(M)$
. From the calculation above we get that
$\mathrm {Aut}(M)$
. From the calculation above we get that
![]() $\mu (\phi (x, a))=0$
for any ergodic measure. By Corollary 2.8,
$\mu (\phi (x, a))=0$
for any ergodic measure. By Corollary 2.8,
![]() $\phi (x,a)$
is universally measure zero.
$\phi (x,a)$
is universally measure zero.
Hence, we get the desired counterexample:
Theorem 5.4. There are
![]() $\omega $
-categorical supersimple theories T of finite
$\omega $
-categorical supersimple theories T of finite
![]() $SU$
-rank with a formula
$SU$
-rank with a formula
![]() $\phi (x, a)$
which does not fork over the empty set, but which is universally measure zero.
$\phi (x, a)$
which does not fork over the empty set, but which is universally measure zero.
Furthermore, by Lemma 4.8, we get a counterexample to the question of Elwes and Macpherson [Reference Elwes, Macpherson, Chatzidakis, Macpherson, Pillay and Wilkie7]:
Corollary 5.5. There are
![]() $\omega $
-categorical supersimple theories T of finite
$\omega $
-categorical supersimple theories T of finite
![]() $SU$
-rank which are not
$SU$
-rank which are not
![]() $MS$
-measurable.
$MS$
-measurable.
The above was also answered in [Reference Evans8, Reference Marimon17], with
![]() $\omega $
-categorical Hrushovski constructions as counterexamples.
$\omega $
-categorical Hrushovski constructions as counterexamples.
Remark 5.6. The point at the heart of our proof is that it is possible to build simple
![]() $\omega $
-categorical Hrushovski constructions which do not satisfy the strong independence theorem. This can be done in different relational languages and with different ranks for the final structure. For example, using a
$\omega $
-categorical Hrushovski constructions which do not satisfy the strong independence theorem. This can be done in different relational languages and with different ranks for the final structure. For example, using a
![]() $3$
-hypergraph, we can build a simple
$3$
-hypergraph, we can build a simple
![]() $\omega $
-categorical Hrushovski construction of
$\omega $
-categorical Hrushovski construction of
![]() $SU$
-rank 1 with non-forking formulas which are universally measure zero.
$SU$
-rank 1 with non-forking formulas which are universally measure zero.
Remark 5.7. As noted after Definition 4.6, for a simple
![]() $\omega $
-categorical structure with
$\omega $
-categorical structure with
![]() $\mathrm {acl}^{eq}(A)=\mathrm {dcl}^{eq}(A)$
, being one-based implies satisfying the strong independence theorem over A. However, satisfying the strong independence theorem over the algebraic closures of finite sets does not imply being one-based: the standard example of a not one-based supersimple
$\mathrm {acl}^{eq}(A)=\mathrm {dcl}^{eq}(A)$
, being one-based implies satisfying the strong independence theorem over A. However, satisfying the strong independence theorem over the algebraic closures of finite sets does not imply being one-based: the standard example of a not one-based supersimple
![]() $\omega $
-categorical Hrushovski construction [Reference Wagner, Kaye and Macpherson24, Example 6.2.27] does satisfy the strong independence theorem over the algebraic closures of finite sets. See [Reference Marimon18] for details. At the moment of writing, we do not know whether satisfying
$\omega $
-categorical Hrushovski construction [Reference Wagner, Kaye and Macpherson24, Example 6.2.27] does satisfy the strong independence theorem over the algebraic closures of finite sets. See [Reference Marimon18] for details. At the moment of writing, we do not know whether satisfying
![]() $F(A)=\mathcal {O}(A)$
for all finite sets implies being one-based.
$F(A)=\mathcal {O}(A)$
for all finite sets implies being one-based.
5.1. Conclusions
Our result makes substantial use of the fact we work with not one-based
![]() $\omega $
-categorical structures. In fact, our counterexample relies on our simple structure not satisfying the strong independence theorem. As we noted in Remark 5.7, for this to be possible we must work with a not one-based structure. This raises two natural questions:
$\omega $
-categorical structures. In fact, our counterexample relies on our simple structure not satisfying the strong independence theorem. As we noted in Remark 5.7, for this to be possible we must work with a not one-based structure. This raises two natural questions:
Question 5.8. Suppose that
![]() $\mathcal {M}$
is a simple
$\mathcal {M}$
is a simple
![]() $\omega $
-categorical structure satisfying the strong independence theorem over the algebraic closures of finite sets. Does this imply that
$\omega $
-categorical structure satisfying the strong independence theorem over the algebraic closures of finite sets. Does this imply that
![]() $F(\emptyset )=\mathcal {O}(\emptyset )$
?
$F(\emptyset )=\mathcal {O}(\emptyset )$
?
Question 5.9. Suppose that
![]() $\mathcal {M}$
is a simple one-based
$\mathcal {M}$
is a simple one-based
![]() $\omega $
-categorical structure. Does this imply that
$\omega $
-categorical structure. Does this imply that
![]() $F(\emptyset )=\mathcal {O}(\emptyset )$
?
$F(\emptyset )=\mathcal {O}(\emptyset )$
?
Regarding Question 5.8, we might also ask whether satisfying some sufficiently strong higher amalgamation property implies
![]() $F(\emptyset )=\mathcal {O}(\emptyset )$
. In this article we have shown that satisfying independent n-amalgamation for all
$F(\emptyset )=\mathcal {O}(\emptyset )$
. In this article we have shown that satisfying independent n-amalgamation for all
![]() $n\in \mathbb {N}$
over finite algebraically closed sets is not sufficient, but an adequate generalisation of the strong independence theorem might work.
$n\in \mathbb {N}$
over finite algebraically closed sets is not sufficient, but an adequate generalisation of the strong independence theorem might work.
For both questions we may also ask whether the hypotheses mentioned (substituting “simple” by “supersimple”) imply
![]() $MS$
-measurability. The finite rank assumption is not needed since supersimple
$MS$
-measurability. The finite rank assumption is not needed since supersimple
![]() $\omega $
-categorical one-based structures are of finite rank [Reference Evans and Wagner10]. In this context, the author’s PhD thesis [Reference Marimon18] provides negative answers to both questions. In particular, we know of an example of a supersimple
$\omega $
-categorical one-based structures are of finite rank [Reference Evans and Wagner10]. In this context, the author’s PhD thesis [Reference Marimon18] provides negative answers to both questions. In particular, we know of an example of a supersimple
![]() $\omega $
-categorical Hrushovski construction of
$\omega $
-categorical Hrushovski construction of
![]() $SU$
-rank
$SU$
-rank
![]() $1$
which is not
$1$
which is not
![]() $MS$
-measurable in spite of satisfying the strong independence theorem over the algebraic closures of finite sets and independent n-amalgamation for all n [Reference Marimon18, Chapter 7.5]. We strongly suspect that some
$MS$
-measurable in spite of satisfying the strong independence theorem over the algebraic closures of finite sets and independent n-amalgamation for all n [Reference Marimon18, Chapter 7.5]. We strongly suspect that some
![]() $\omega $
-categorical Hrushovski construction will yield an example of a structure with
$\omega $
-categorical Hrushovski construction will yield an example of a structure with
![]() $F(\emptyset )\subsetneq \mathcal {O}(\emptyset )$
while satisfying the strong independence theorem (and arbitrarily strong higher amalgamation properties). Meanwhile, the universal homogeneous tetrahedron-free
$F(\emptyset )\subsetneq \mathcal {O}(\emptyset )$
while satisfying the strong independence theorem (and arbitrarily strong higher amalgamation properties). Meanwhile, the universal homogeneous tetrahedron-free
![]() $3$
-hypergraph is not
$3$
-hypergraph is not
![]() $MS$
-measurable in spite of being
$MS$
-measurable in spite of being
![]() $\omega $
-categorical supersimple and one-based [Reference Marimon18, Chapter 7.3]. If one could prove that
$\omega $
-categorical supersimple and one-based [Reference Marimon18, Chapter 7.3]. If one could prove that
![]() $F(\emptyset )\subsetneq \mathcal {O}(\emptyset )$
for this structure we would answer negatively both questions.
$F(\emptyset )\subsetneq \mathcal {O}(\emptyset )$
for this structure we would answer negatively both questions.
On the other hand, we do not know whether being
![]() $\omega $
-categorical and
$\omega $
-categorical and
![]() $MS$
-measurable implies being one-based. Indeed, this question was also asked by Elwes and Macpherson in [Reference Elwes, Macpherson, Chatzidakis, Macpherson, Pillay and Wilkie7]. In a more general context, it is unclear whether one might be able to show that forking and being universally measure zero disagree for not one-based supersimple
$MS$
-measurable implies being one-based. Indeed, this question was also asked by Elwes and Macpherson in [Reference Elwes, Macpherson, Chatzidakis, Macpherson, Pillay and Wilkie7]. In a more general context, it is unclear whether one might be able to show that forking and being universally measure zero disagree for not one-based supersimple
![]() $\omega $
-categorical structures:
$\omega $
-categorical structures:
Question 5.10. Suppose that
![]() $\mathcal {M}$
is supersimple
$\mathcal {M}$
is supersimple
![]() $\omega $
-categorical with
$\omega $
-categorical with
![]() $F(A)=\mathcal {O}(A)$
for all finite
$F(A)=\mathcal {O}(A)$
for all finite
![]() $A\subset M$
. Is
$A\subset M$
. Is
![]() $\mathcal {M}$
one-based?
$\mathcal {M}$
one-based?
By Lemma 4.8, a positive answer to this question would imply that all
![]() $\omega $
-categorical
$\omega $
-categorical
![]() $MS$
-measurable structures are one-based, answering the question of Elwes and Macpherson.
$MS$
-measurable structures are one-based, answering the question of Elwes and Macpherson.
Acknowledgements
This article was written during my PhD at Imperial College London under the supervision of David Evans and Charlotte Kestner, both of whom I thank for their support and help. Nicholas Ramsey gave an excellent talk at Imperial about [Reference Chernikov, Hrushovski, Kruckman, Krupiński, Moconja, Pillay and Ramsey3], which motivated me to look at whether
![]() $\omega $
-categorical Hrushovski constructions may also have been a counterexample. I am also grateful to my friend Matteo Tabaro for helpful discussions during my learning of ergodic theory. Finally, some of the ideas behind this article are greatly indebted to Ehud Hrushovski and his unpublished article [Reference Hrushovski11], which he kindly shared with me.
$\omega $
-categorical Hrushovski constructions may also have been a counterexample. I am also grateful to my friend Matteo Tabaro for helpful discussions during my learning of ergodic theory. Finally, some of the ideas behind this article are greatly indebted to Ehud Hrushovski and his unpublished article [Reference Hrushovski11], which he kindly shared with me.
Funding
The author’s PhD was supported by an Admin Roth Scholarship funded by the Department of Mathematics of Imperial College London. This research is also funded by the European Union (ERC, POCOCOP, 101071674). Views and opinions expressed are, however, those of the author only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them.