Let Ω be an algebraic number field, and let NΩ ⊂ ℚ be the group of norms of fractional ideals of Ω. Then NΩ is a subgroup of the positive rationals; the latter is the direct sum of a denumerable infinity of infinite cyclic groups, and so it is free abelian; thus NΩ is free abelian, and, since it is not finitely generated, we must have 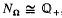 qua abstract groups. The purpose of this paper is, in the first place, to find a “metrical ” way of distinguishing these isomorphic groups, and, to this end, we introduce the notion of Farey density, defined as follows; let X be a positive integer, and consider the Farey section ℱ(X) of order X, thus the set of all reduced positive fractions with denominator < X; then the quotient
qua abstract groups. The purpose of this paper is, in the first place, to find a “metrical ” way of distinguishing these isomorphic groups, and, to this end, we introduce the notion of Farey density, defined as follows; let X be a positive integer, and consider the Farey section ℱ(X) of order X, thus the set of all reduced positive fractions with denominator < X; then the quotient
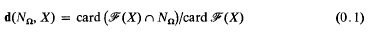
measures the proportion of elements of ℱ(X) which are in NΩ, and, as X → ∞, it gives a measure of the “density ” of fractional ideal norms in the rational interval (0, 1).