Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T21:56:11.758Z Has data issue: false hasContentIssue false
  • English
  • Français

The Farey density of norm subgroups in global fields (I)

Published online by Cambridge University Press:  26 February 2010

R. W. K. Odoni
R. W. K. Odoni
Affiliation:
Department of Mathematics, The University of Glasgow
Get access

Extract

Let Ω be an algebraic number field, and let NΩ ⊂ ℚ be the group of norms of fractional ideals of Ω. Then NΩ is a subgroup of the positive rationals; the latter is the direct sum of a denumerable infinity of infinite cyclic groups, and so it is free abelian; thus NΩ is free abelian, and, since it is not finitely generated, we must have 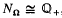qua abstract groups. The purpose of this paper is, in the first place, to find a “metrical ” way of distinguishing these isomorphic groups, and, to this end, we introduce the notion of Farey density, defined as follows; let X be a positive integer, and consider the Farey section ℱ(X) of order X, thus the set of all reduced positive fractions with denominator < X; then the quotient

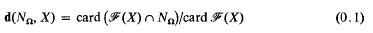
measures the proportion of elements of ℱ(X) which are in NΩ, and, as X → ∞, it gives a measure of the “density ” of fractional ideal norms in the rational interval (0, 1).

Type
Research Article
Information
Mathematika , Volume 20 , Issue 2 , December 1973 , pp. 155 - 169
Copyright
Copyright © University College London 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Landau, E., Handbuch der Primzahlverteilung (Teubner, Leipzig, 1909), Vol. 2, 643–644.Google Scholar
2. Wirsing, E., Kongress der Deutsche Math. Vereinigung, 1955.Google Scholar
3. Ostmann, H., Additive Zahlentheorie (Springer, 1956), Vol. 2, 67.Google Scholar
4. Frohlich, A., “The genus field and genus group for finite number fields”, Mathematika, 6 (1959, 40–46.CrossRefGoogle Scholar
5. Artin, E., “Über die Zetafunktionen gewisser algebraischen Zahlkörper”, Math. Annalen, 89 (1923).CrossRefGoogle Scholar
6. Hasse, H., Bericht uber neuere Untersuchungen und Probleme aus der Theorie der algebraischer Zahlkörper (Physica-Verlag, Wiirzburg, 1965), Vol. 2, 126.CrossRefGoogle Scholar
7. Hasse, H., Bericht uber neuere Untersuchungen und Probleme aus der Theorie der algebraischer Zahlkörper (Physica-Verlag, Wiirzburg, 1965), Vol. 2, 149 et seq.CrossRefGoogle Scholar
8. Brauer, R., “On Artin's L-series with general group characters”, Annals of Maths., (2), 48, 502–504.CrossRefGoogle Scholar
9. Landau, E., “Über der Verteilung der Primideale in den Idealklassen eines algebraischen Zahl- körpers”, Math. Annalen, 63 (1907), 145–204.CrossRefGoogle Scholar
10. Hardy, G. H. and Riesz, M., The general theory of Dirichlet series, Cambridge Tract, 18 (Cambridge 1915), 11–14.Google Scholar
11. Whittaker, E. T. and Watson, G. N., Course of modern analysis (Cambridge, 1927), Ch. 12, 244–245.Google Scholar
12. Hasse, H., loc. sit (6), Vol. 1, p. 5 et seq.Google Scholar
13. Hasse, H., loc. sit (6), Vol. 2, p. 23.Google Scholar
14. Hardy, G. H. and Wright, E. M., The theory of numbers, 4th ed. (Oxford, 1960).Google Scholar
15. Pall, Gordon, “The distribution of integers represented by binary quadratic forms”, Bull Amer. Math. Soc, 49 (1943), 447–449.CrossRefGoogle Scholar
16. Bernays, P., “Ueber die Darstellung ... durch primitiven, binären Quadratischen Formen ”, Dissertation (Göttingen, 1912).Google Scholar
17. Luthar, I. S.,“Generalisation of a theorem of Landau”, Ada Arithmetica, 12 (1966–67), 223–228.CrossRefGoogle Scholar