Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T19:31:16.007Z Has data issue: false hasContentIssue false
  • English
  • Français

On the largest prime factor of p+a

Published online by Cambridge University Press:  26 February 2010

C. Hooley
C. Hooley
Affiliation:
University College of South Wales and Monmouthshire, Cardiff, Wales
Get access

Extract

Among several interesting analogues of Chebyshev's problem about the largest prime factor of

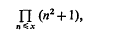
there is the question of the largest prime factor of

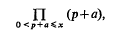
where a is a given non-zero integer and the product is taken over positive primes p. The latter subject appears to have been first treated by Goldfeld [2] and Motohashi [6], who showed that, if Px be the greatest prime factor in question, then there exists a constant 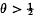such that Px > xθ for all sufficiently large x. Their method, which involved the use of both Bombieri's theorem and the Brun-Titchmarsh theorem, had some affinity with the earlier treatments of Chebyshev's original problem.

Type
Research Article
Information
Mathematika , Volume 20 , Issue 2 , December 1973 , pp. 135 - 143
Copyright
Copyright © University College London 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Gallagher, P. X., “The large sieve”, Mathematika, 14 (1967), 14–20.CrossRefGoogle Scholar
2. Goldfeld, M.,“On the number of primes p for which p+a has a large prime factor“, Mathematika, 16 (1969), 23–27.CrossRefGoogle Scholar
3. Hooley, C., “On the greatest prime factor of a quadratic polynomial”, Acta Mathematica, 117 (1967), 281–299.CrossRefGoogle Scholar
4. Hooley, C., “On the Brun-Titchmarsh theorem”, J. für die reine und angewandte Mathematik, 255 (1972), 60–79.Google Scholar
5. Montgomery, H. L., Topics in multiplicative number theory (Springer).Google Scholar
6. Motohashi, Y., “A note on the least prime in an arithmetic progression with a prime difference”, Ada Arith., 17 (1970), 283–285.CrossRefGoogle Scholar
7. Selberg, A., “On an elementary method in the theory of primes”, Norske vid. Selsk. Forh., Trondhjem, 19 (1947), 64–67.Google Scholar