2 Magnetic fields, electromotive force and electrical currents in a conducting cylinder

In Bisnovatyi-Kogan & Glushikhina (Reference Bisnovatyi-Kogan and Glushikhina2018a), the following general relations in Cartesian coordinates were written for the four kinetic coefficients, namely heat conductivity ($\lambda _{ij}$), diffusion ($\eta _{ij}$), thermodiffusion ($\mu _{ij}$) and diffusional thermal effect ($\nu _{ij}$) of electrons in non-degenerate non-relativistic plasma, that depends on magnetic field $B_i$, concentration of electrons $n_e$, electric field $E_i$, temperature $T$ and mass-average velocity $c_{0k}$:

(2.1)\begin{gather} q_i=q_{i}^{(T)}+q_{i}^{(D)} =-(\lambda^{(1)}\delta_{ij}-\lambda^{(2)} \varepsilon_{ijk}B_k+\lambda^{(3)}B_i B_j)\frac{\partial T}{\partial x_j} \nonumber\\ \quad -n_e (\nu^{(1)}\delta_{ij}-\nu^{(2)}\varepsilon_{ijk}B_k+\nu^{(3)}B_i B_j)d_j, \end{gather}

(2.2)\begin{gather} \langle v_{i} \rangle = \langle v_{i}^{(D)} \rangle + \langle v_{i}^{(T)} \rangle \nonumber\\ =-n_e (\eta^{(1)}\delta_{ij}-\eta^{(2)}\varepsilon_{ijk}B_k+\eta^{(3)}B_i B_j)d_j \nonumber\\ \quad\ \ -(\mu^{(1)}\delta_{ij}-\mu^{(2)}\varepsilon_{ijk}B_k+\mu^{(3)}B_i B_j)\frac{\partial T}{\partial x_j}, \end{gather}

(2.3)\begin{gather} d_{i} = \frac{\rho_{N}}{\rho} \frac{ \partial \ln P_{e}}{\partial x_{i}} - \frac{\rho_{e}}{P_{e}}\frac{1}{\rho}\frac{\partial P_{N}}{\partial x_{i}} +\frac{e}{kT}\left(E_i+\frac{1}{c} \varepsilon _{ikl} c_{0k} B_{l}\right). \end{gather}

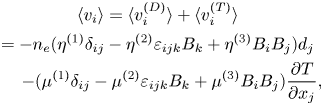
The indices $(T)$ and $(D)$ correspond to the heat flux $q_i$, and diffusion velocity $\langle v_{i} \rangle$ of electrons, determined by temperature gradient $\partial T/\partial x_j$, and diffusion vector $d_j$, respectively.

Here $P_e$ is the electron pressure, $P_N$ is the ion pressure, $\rho$ is the density, defined as $\rho = m_N n_N$, $n_N$ is the concentration of ions. The tensor kinetic coefficients $\lambda ^{(i)}$, $\mu ^{(i)}$, $\eta ^{(i)}$ and $\nu ^{(i)}$ determine the heat and diffusion fluxes in the following directions. The upper indices $^{(1)}$ determine the above-mentioned fluxes along the temperature gradient $\partial T/\partial x_i$, or diffusion vector $d_i$. The upper indices $^{(3)}$ are related to the direction along the magnetic field; and the upper indices $^{(2)}$ determine fluxes perpendicular to the plane defined by the magnetic field vector $B_i$ and any of the vectors $\partial T/\partial x_i$ or $d_i$. These last fluxes are referred to as the Hall ones, $q_{{\rm Hall}}$ and $j_{{\rm Hall}}$. We consider here terms in the heat flux and the electrical current produced by the temperature gradient only, so (2.1) and (2.2) can be written as

(2.4)\begin{gather} q_i=q_{i}^{(T)}=-(\lambda^{(1)}\delta_{ij}-\lambda^{(2)}\varepsilon_{ijk}B_k+\lambda^{(3)}B_i B_j) \frac{\partial T}{\partial x_j}, \end{gather}

(2.5)\begin{gather}\langle v_{i} \rangle=\langle v_{i}^{(T)} \rangle =-(\mu^{(1)}\delta_{ij}-\mu^{(2)}\varepsilon_{ijk}B_k+\mu^{(3)}B_i B_j) \frac{\partial T}{\partial x_j}. \end{gather}

Let us consider a plasma cylinder (see figures 1 and 2) with a uniform magnetic field $B$ along the $z$ axis, and a temperature gradient vector along the radius. In the case of a cylinder symmetry ${\partial }/{\partial z}={\partial }/{\partial \phi }=0$, the only non-zero parameters are $q_r, q_\phi, j_r, j_\phi, B_z$. Using the definition of the electrical current

(2.6)\begin{equation} j_i =-n_e e \langle v_i \rangle, \end{equation}

we obtain from (2.4) and (2.5) the following relations:

(2.7a–c)\begin{gather} q_r=-\lambda^{(1)}\frac{{\rm d} T}{{\rm d} r},\quad q_\phi=-B_z\left(\lambda^{(2)}\frac{{\rm d} T}{{\rm d} r}\right),\quad q_z =0, \end{gather}

(2.8a–c)\begin{gather}j_r=- e n_e\left(\mu^{(1)}\frac{{\rm d} T}{{\rm d} r}\right),\quad j_\phi=- en_eB_z\left(\mu^{(2)}\frac{{\rm d} T}{{\rm d} r}\right),\quad j_z=0. \end{gather}

Figure 1. Conducting cylinder with Hall current $j_{{\rm Hall}}$, depending on the magnitude of the radial temperature gradient and external constant magnetic field $B_0$ along its axis. The induced magnetic field $B_1$ is determined by the Hall current. Here $R_1$ is the radius of the central heated region with constant temperature $T_0$. The toroidal region, coloured in grey, contains Hall current and associated magnetic field, which has an opposite direction to the external field $B_0$, decreasing the resulting field along the cylinder.

Figure 2. The same cylinder as in figure 1, with opposite direction of the constant magnetic field $B_0$. We see that the magnetic field $B_1$, induced by Hall currents $j_{{\rm Hall}}$ is again opposite to the direction of $B_0$. Therefore, the resulting magnetic field decreases, for any direction of the magnetic field $B_0$.

Figures 1 and 2 have opposite directions of the initial magnetic field $B_0$. In both cases this field is deceasing due to the action of the Hall current. The same decrease of $B_z$ remains in the opposite direction of the heat flux, with heating of the outer boundary of the cylinder.

The Lorentz approximation is applied when the mass of light particles (electrons) is much smaller than the mass of heavy particles (ions or nuclei), and in addition electron–electron collisions are neglected. In this approximation the linearized Boltzmann equation, from which kinetic coefficients are derived, has an exact solution at zero magnetic field. In different approaches the solution in Lorentz approximation was considered by Chapmen & Cowling (Reference Chapmen and Cowling1952) (p. 187), see also Schatzman (Reference Schatzman1958) and Bisnovatyi-Kogan (Reference Bisnovatyi-Kogan2001).

The explicit exact solution in Lorentz approximation is obtained for the case of a zero magnetic field. The heat flux connected only with the temperature gradient, is given in Schatzman (Reference Schatzman1958) and Bisnovatyi-Kogan (Reference Bisnovatyi-Kogan2001):

(2.9a,b)\begin{equation} q^T_i=-\tilde\lambda_T \frac{\partial{T}}{\partial x_{i}},\quad \tilde\lambda_T= \frac{320}{3{\rm \pi}}\frac{k^2 Tn_e}{m_e}\tau_e. \end{equation}

For the average velocity we can write the expression in the Lorentz approximation (Glushikhina Reference Glushikhina2020) with the thermal diffusion for the non-degenerate case:

(2.10a,b)\begin{equation} \langle v_i^{T}\rangle=-\mu^{l}\frac{\partial{T}}{\partial x_{i}},\quad \mu^{l}\equiv \frac{\sigma_T}{en_e} = \frac{16k}{m_e {\rm \pi}}\tau_e. \end{equation}

Using the expression for the electric current density, we obtain the thermodiffusion part in the form

(2.11)\begin{equation} j_i^T =-n_e e \langle v_i^T \rangle =-\sigma_T \frac{\partial T}{\partial x_i}. \end{equation}

We use here the parameters: electron Larmor frequency $\omega _B$; the time between $eN$ collisions $\tau _e$; and thermal electrical conductivity coefficient $\sigma _T$; which in the non-degenerate Lorentz gas approximation are determined as (Bisnovatyi-Kogan Reference Bisnovatyi-Kogan2001)

(2.12)\begin{equation} \left.\begin{gathered} \omega_B=\frac{eB}{m_e c},\quad \tau_{e}=\frac{3}{4}\sqrt{\frac{m_e}{2{\rm \pi}}} \frac{(kT)^{3/2}}{Z^2{e}^4n_N\varLambda}, \\ \sigma_T = e n_e \mu_{e}=\frac{6\sqrt{2}}{{\rm \pi}^{3/2}\varLambda} \frac{e n_e k^2 T}{n_N e^4 Z^2}\left(\frac{kT}{m_e}\right)^{1/2} = \frac{16k e n_e}{m_e {\rm \pi}}\tau_e. \end{gathered}\right\} \end{equation}

Here $n_e, n_N$ are concentrations of electrons and nuclei with atomic number $Z$; $\varLambda$ is a Coulomb logarithm. The microscopic process of binary collision is not disturbed here by the magnetic field. For a very large magnetic field this approximation is not exact, but it does not change qualitatively the macroscopic behaviour of the system (Braginskii Reference Braginskii1958a).

Components of the kinetic coefficient's tensor in the presence of the magnetic field can be expressed using the kinetic coefficient in Lorentz approximation. In particular for thermal electrical conductivity with a $B_z$ magnetic field, the conductivity along magnetic field lines is $\sigma _T$, and across magnetic field lines it is equal to $\sigma _T/(1+\omega _{B}^{2}\tau _{e}^{2})$ In the Hall direction, that is perpendicular to the plane defined by $B_z$ and $\partial T/ \partial x$ the conductivity is written as $\sigma _T \omega _{B} \tau _{e}/(1+\omega _{B}^{2}\tau _{e}^{2})$ (Chapmen & Cowling Reference Chapmen and Cowling1952) (p. 322, p. 338). Hence components of the electrical current density vector $\boldsymbol {j}$ in a cylinder with $B_z$ and temperature gradient vector along the radius are determined as

(2.13)\begin{equation} \left.\begin{gathered} j_r=-\frac{\sigma_T (\boldsymbol{\nabla}T)_r}{1+\omega_B^2\tau_e^2}, \\ j_\varphi=-\frac{(\sigma_T(\boldsymbol{\nabla}T)_r ) \omega_B\tau_e }{1+\omega_B^2\tau_e^2},\quad j_z=0. \end{gathered}\right\} \end{equation}

The connection of vectors $\boldsymbol {j_\phi }$ and induced field $\boldsymbol {B}$ is determined by the Maxwell equations.

3 Model description, solutions and results

From Maxwell equations we obtain the following relations for the magnetic field components in the cylinder:

(3.1a,b)\begin{equation} B_r=B_\varphi=0,\quad \frac{c}{4{\rm \pi}}\frac{{\rm d} B_z}{{\rm d} r}= \frac{\sigma_T(\boldsymbol{\nabla}T)_r \omega_B\tau_e }{1+\omega_B^2\tau_e^2}. \end{equation}

The magnetic field $B_z$ in the cylinder consists of the constant component $B_0$, created by external source, and the field $B_{1}$, created by electrical current inside the cylinder:

(3.2)\begin{equation} B_z=B_0+B_1. \end{equation}

Let us consider a stationary state of the cylinder with a constant radial heat flux $Q$. The radial heat flux density is written now as

(3.3)\begin{equation} q_r=\frac{Q}{2 {\rm \pi}r}=-\tilde\lambda_T\frac{(\boldsymbol{\nabla} T)_r}{1+(\omega_B \tau_e)^2}. \end{equation}

This equation should be solved in combination with the equation for $B_z$ written as

(3.4)\begin{equation} \frac{{\rm d} B_z}{{\rm d} r}=\frac{4 {\rm \pi}}{c}\frac{\sigma_T(\boldsymbol{\nabla}T)_r \omega_B\tau_e }{1+(\omega_B\tau_e)^2}. \end{equation}

Using $(\boldsymbol {\nabla } T)_r$ from (3.3), we obtain the dependencies of the magnetic field derivative on the temperature, using (1.1), in the form

(3.5)\begin{equation} \frac{{\rm d} B_z}{{\rm d} r} =-\frac{3 Q \omega_B \tau_e e}{10 kT c r}. \end{equation}

Equations (3.3) and (3.5) cannot be extended on the axis with $r = 0$ because of singularities at zero radius. It is suggested in this problem, that the only source of heat is situated near the axis of the cylinder, and is represented by a uniformly heated cylinder with radius $R_1 << R_0$, where $R_0$ is the outer radius of the cylinder.

Equations (3.3) and (3.5) are solved jointly under boundary conditions $B_z(R_1)=B_0, \quad T(R_0)=T_0$, at given parameter $Q$. Introducing non-dimensional Hall component $b_1$ as $B_1 = B_0 b_1$, taking into account the definition $\omega _{B} = {eB_z}/{m_e c} = {e(B_0 +B_1)}/{m_e c} = \omega _{B0} (1+ b_1)$ and $x = {r}/{R_0}$ we write the (3.5) in the form

(3.6)\begin{equation} \frac{{\rm d} b_1}{{\rm d}x}=- \frac{3 e Q \tau_e }{10 k c T B_{0} x} \omega_{B0} (1+ b_1). \end{equation}

Equation (3.3) may be written in the following form:

(3.7)\begin{equation} Q = \frac{-\tilde\lambda_T (\boldsymbol{\nabla} T)_{r} 2 {\rm \pi}r}{1+\omega^2_{B0} \tau^2_{e} (1+b_1)^{2}}. \end{equation}

Assuming in (3.6) constant ratio $\tau _e/T = F$, then (3.5) takes the form

(3.8)\begin{equation} \frac{{\rm d} b_1}{{\rm d}x}=-\frac{3 e Q F}{10 c k B_0 x }\omega_{B0}(1+b_1),\quad 1> x>x_1 = \frac{R_1}{R_0},\quad b_1(x_1) = 0. \end{equation}

The analytical solution of (3.8) is written as

(3.9a,b)\begin{equation} b_1 =\left(\frac{x_1}{x}\right)^{\gamma} - 1,\quad \gamma = \frac{3 e QF}{10 k c B_0}\omega_{B0}. \end{equation}

The value of $b_1$ is approaching $(-1)$ at $x_1 \to 0$. In the case of a plasma cylinder with parameters from (2.12), the equations (3.6) and (3.7), determining the Hall component $b_1$, are written as follows:

(3.10)\begin{equation} \left.\begin{gathered} \frac{{\rm d} b_1}{{\rm d}x}=- \frac{3 e Q}{10 k c B_0 x } \omega_{B0} (1+ b_1) C_1 T^{1/2}, \\ \frac{{\rm d} T}{{\rm d}x}=-\frac{1+ C_1^{2} T^{3} \omega_{B0}^2(1+b_1)^2}{2 {\rm \pi}x C_2 T^{5/2}} Q . \end{gathered}\right\} \end{equation}

The constants $C_1$ and $C_2$ are determined from relations

(3.11)\begin{gather} \tau _e = \frac{3(kT)^{3/2}}{4Z^2 e^4 n_N \varLambda}\sqrt{\frac{m_e}{2 {\rm \pi}}} = C_1T^{3/2}, \end{gather}

(3.12)\begin{gather}\tilde \lambda_T = \frac{20 kT\sigma_T}{3 e} = \frac{40 \sqrt{2} k n_e}{{\rm \pi}^{3/2}\varLambda n_N}\left( \frac{kT}{e^2 Z}\right)^{2} \left( \frac{kT}{m_e} \right)^{1/2} = C_2 T^{5/2} \end{gather}

so that

(3.13a,b)\begin{equation} \omega_B=\omega_{B0}(1+b_1),\quad \omega_{B}\tau_e=C_1 T^{3/2}\omega_{B0}(1+b_1). \end{equation}

Let us introduce dimensionless parameters:

(3.14a–d)\begin{equation} {\tilde T}=\frac{T}{T_0},\quad N = \frac{3 e Q\omega_{B0} C_1}{10 kcB_0}T_0^{1/2},\quad G = C_1^{2} T_0^3 \omega_{B0}^{2},\quad E=\frac{2{\rm \pi} C_2 T_0^{7/2}}{Q}. \end{equation}

Equations (3.10) have following form with new parameters:

(3.15a,b)\begin{equation} \frac{{\rm d} b_1}{{\rm d}x} =-N\frac{(1+b_1){\tilde T}^{1/2}}{x},\quad \frac{{\rm d}\tilde T}{{\rm d}x}=-\frac{1+G (1+b_1)^2 {\tilde T^3}}{x E {\tilde T^{5/2}}}. \end{equation}

We solve (3.13a,b) numerically in the interval $x_1\leq x\leq 1$ at boundary conditions

(3.16a,b)\begin{equation} b_1(x_1) = 0,\quad \tilde T(x_1) = 1. \end{equation}

Results of the solution are presented in the figures 3–8 for the case of plasma parameters in the NS crust.

Figure 3. Magnetic field in the cylinder, induced by the Hall current, for $F = 5.2\times 10^{-5}$, $E = 0.012$ and three values of $N$: $N_1 = 6.0$; $N_2 = 0.6$; $N_3 = 6.0\times 10^{-2}$. These values are related to $Z = 26$, and include combinations $B_{0} = 10^{12}\ \textrm {G},\ T_0 = 10^{9}\ \textrm {K},\ \rho _0 = 10^{7}$ g cm$^{-3}$ for $N_1$; $B_{0} = 10^{13}\ \textrm {G}, T_0 = 10^{9}\ \textrm {K},\ \rho _0 = 10^{8}$ g cm$^{-3}$ for $N_2$; $B_{0} = 10^{14}\ \textrm {G},\ T_0 = 10^{9}\ \textrm {K}, \rho _0 = 10^{9}$ g cm$^{-3}$ for $N_3$.

Figure 4. Temperature distribution in the cylinder for the same parameters as in figure 3.

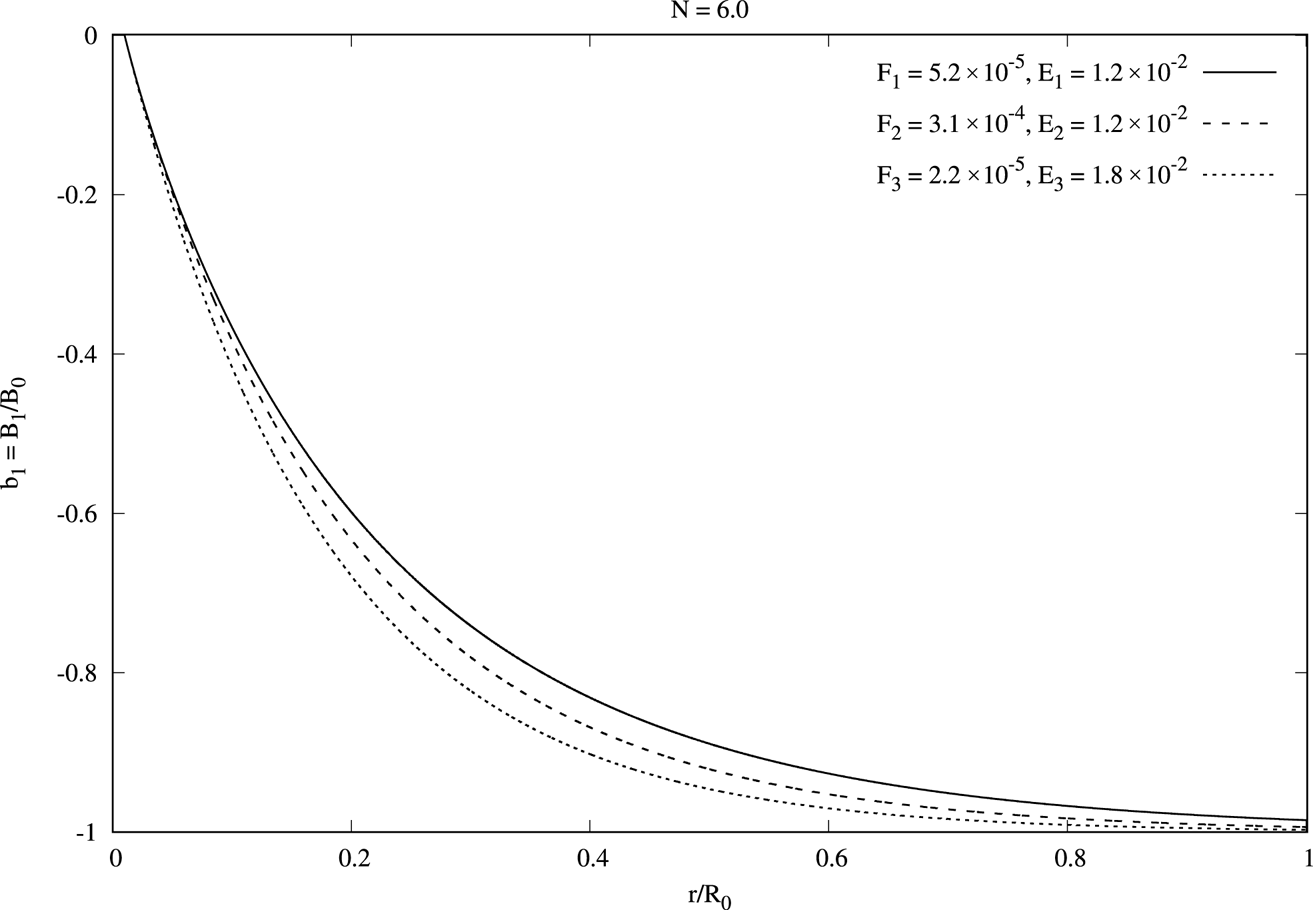
Figure 5. Magnetic field in the cylinder, induced by the Hall current, for $N = 6$ and three variants: $F_1 = 5.2\times 10^{-5},\ E_1 = 0.012$; $F_2 = 3.1\times 10^{-4},\ E_2 = 0.012$; $F_3 = 2.2\times 10^{-5},\ E_3 = 0.018$. These values are related to $Z = 26$, and include combinations $B_{0} = 10^{12}\ \textrm {G},\ T_0 = 10^{9}\ \textrm {K},\ \rho _0 = 10^{7}$ g cm$^{-3}$ for $F_1$, $E_1$; $B_{0} =10^{13}\ \textrm {G},\ T_0 = 1.8\times 10^{9}\ \textrm {K}, \rho _0 = 10^{8}$ g cm$^{-3}$ for $F_2$, $E_2$; $B_{0} = 10^{13}\ \textrm {G},\ T_0 = 3.5\times 10^{9}\ \textrm {K},\ \rho _0 = 10^{9}$ g cm$^{-3}$ for $F_3$, $E_3$.

Figure 6. Temperature distribution in the cylinder for the same parameters as in figure 5.

Figure 7. Magnetic field in the cylinder, induced by the Hall current, for $E=0.012$, and three variants: $F_1=5.1\times 10^{-3},N_1=6.0$; $F_2=5.1\times 10^{-5},N_2=0.6$; $F_3=5.1\times 10^{-7},\ N_3 =0.06$. These values are related to $Z = 26$, and include combinations $B_{0} = 10^{13}\ \textrm {G},\ T_0 = 10^{9}\ \textrm {K},\ \rho _0 = 10^{7}$ g cm$^{-3}$ for $F_1$, $N_1$; $B_{0} =10^{13}\ \textrm {G},\ T_0 =10^{9}\ \textrm {K},\ \rho _0 = 10^{8}$ g cm$^{-3}$ for $F_2$, $N_2$; $B_{0} = 10^{13}\ \textrm {G},\ T_0 =10^{9}\ \textrm {K},\ \rho _0 = 10^{9}$ g cm$^{-3}$ for $F_3$,$N_3$.

Figure 8. Temperature distribution in the cylinder for the same parameters as in figure 7.

Equation (3.13a,b) can be used for analysing the magnetized plasma in laboratory facilities. Results of these calculations are presented in the figures 9–14.

Figure 9. Magnetic field in the cylinder, induced by the Hall current, for $F=1.2\times 10^{-5}$, $E=0.1$, and three variants: $N=0.8$; $N_2=8.5$; $N_3=85.2$. These values are related to $Z =1$ and include combinations $B_{0} = 5\times 10^3$ G, $T_0 =2\times 10^{5}$ K, $\rho _0=10^{-4}$ g cm$^{-3}$ for $N_1$; $B_{0}=5\times 10^{2}$ G, $T_0 = 2\times 10^{5}$ K, $\rho _0 = 10^{-5}$ g cm$^{-3}$ for $N_2$; $B_{0}=50$ G, $T_0 = 2\times 10^{5}$ K, $\rho _0=10^{-6}$ g cm$^{-3}$ for $N_3$.

Figure 10. Temperature distribution in the cylinder for the same parameters as in figure 9.

Figure 11. Magnetic field in the cylinder, induced by the Hall current, for $E = 0.1$ and three variants: $F_1= 1.3\times 10^{-11}$, $N_1=0.085$; $F_2=1.3\times 10^{-9}$, $N_2=0.8$; $F_3=1.3\times 10^{-7}$, $N_3=8.5$. These values are related to $Z = 1$, and include variants $T_0 = 2\times 10^{5}$ K, $B_{0}= 50$ G, $\rho _0=10^{-3}$ g cm$^{-3}$ for $N_1$, $F_1$; $\rho _0 = 10^{-4}$ g cm$^{-3}$ for $N_2$, $F_2$; $\rho _0 = 10^{-5}$ g cm$^{-3}$ for $N_3$ $F_3$.

Figure 12. Temperature distribution in the cylinder for the same parameters as in figure 11.

Figure 13. Magnetic field in the cylinder, induced by the Hall current, $N = 0.8,\ E=0.1$ and three variants: $F_1 = 4.7\times 10^{-5}$; $F_2 = 4.7\times 10^{-7}$; $F_3 = 4.7\times 10^{-9}$. These values are related to $Z = 1$, and include variants $\rho =10^{-4}$ g cm$^{-3}$, $T_0 = 2\times 10^{5}\ \textrm {K}$, $B_{0} = 10^{4}$ G, for $F_1$; $B_{0} =10^{3}$ G, for $F_2$; $B_{0} =10^{2}$ G, for $F_3$.

Figure 14. Temperature distribution in the cylinder for the same parameters as in figure 13.