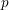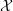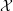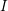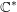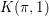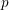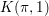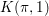Research Article
Beyond endoscopy via the trace formula: 1. Poisson summation and isolation of special representations
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2015, pp. 1791-1820
-
- Article
- Export citation
On the smooth transfer for Guo–Jacquet relative trace formulae
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2015, pp. 1821-1877
-
- Article
- Export citation
A mirror theorem for toric stacks
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2015, pp. 1878-1912
-
- Article
-
- You have access
- Open access
- Export citation
Purity for graded potentials and quantum cluster positivity
- Part of:
-
- Published online by Cambridge University Press:
- 19 May 2015, pp. 1913-1944
-
- Article
- Export citation
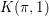 $K({\it\pi},1)$-neighborhoods and comparison theorems
$K({\it\pi},1)$-neighborhoods and comparison theorems
- Part of:
-
- Published online by Cambridge University Press:
- 05 June 2015, pp. 1945-1964
-
- Article
- Export citation
Le complémentaire des puissances
 $n$-ièmes dans un corps de nombres est un ensemble diophantien
$n$-ièmes dans un corps de nombres est un ensemble diophantien
- Part of:
-
- Published online by Cambridge University Press:
- 22 June 2015, pp. 1965-1980
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
COM volume 151 Issue 10 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 October 2015, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
COM volume 151 Issue 10 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 October 2015, pp. b1-b2
-
- Article
-
- You have access
- Export citation