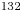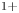1. Introduction
The cooling (Larson Reference Larson1995) of secondary beams of particles (which is often required for their efficient transport through accelerators towards detectors) can not be achieved with standard beam transport elements due to Liouville's theorem (Reiser & O-Shea Reference Reiser and O-Shea2008), so that suitable methods, such as gas filled beam guides (Herfurth et al. Reference Herfurth, Dilling, Kellerbauer, Bollen, Henry, Kluge, Lamour, Lunney, Moore and Scheidenberger2001), are needed. In the case of unstable nucleus ions produced in a thick fission target, $^{132}$![]() Sn$^{1+}$
Sn$^{1+}$![]() for example (Nieminen et al. Reference Nieminen, Huikari, Jokinen, Äystö, Campbell and Cochrane2001), the initial root mean square (r.m.s.) energy spread $\sigma _E^{{\rm in}}$
for example (Nieminen et al. Reference Nieminen, Huikari, Jokinen, Äystö, Campbell and Cochrane2001), the initial root mean square (r.m.s.) energy spread $\sigma _E^{{\rm in}}$![]() at plasma ion sources is approximately 5 eVr.m.s. (Penescu et al. Reference Penescu, Catherall, Lettry and Stora2010; Catherall et al. Reference Catherall, Andreazza, Breitenfeldt, Dorsival, Focker, Gharsa, Giles, Grenard, Locci and Martins2017). Therefore, adequate cooling can be provided by gas collisions in radiofrequency quadrupole (RFQ) coolers (RFQCs), within a 1 m typical length. The r.m.s. beam emittance is also affected by collisions and RQFC beam transport, especially at extraction, as shown in this paper, where the installation of a prototype RFQC into a solenoid magnet as well as related simulations and theoretical tools are described.
at plasma ion sources is approximately 5 eVr.m.s. (Penescu et al. Reference Penescu, Catherall, Lettry and Stora2010; Catherall et al. Reference Catherall, Andreazza, Breitenfeldt, Dorsival, Focker, Gharsa, Giles, Grenard, Locci and Martins2017). Therefore, adequate cooling can be provided by gas collisions in radiofrequency quadrupole (RFQ) coolers (RFQCs), within a 1 m typical length. The r.m.s. beam emittance is also affected by collisions and RQFC beam transport, especially at extraction, as shown in this paper, where the installation of a prototype RFQC into a solenoid magnet as well as related simulations and theoretical tools are described.
Cooling (van der Meer Reference van der Meer1987; Larson Reference Larson1995) is also critical to accelerator-based sub-nuclear physics, with secondary beams ranging from positrons $e^+$![]() (Siemann Reference Siemann1992) to muons $\mu ^\pm$
(Siemann Reference Siemann1992) to muons $\mu ^\pm$![]() (Neuffer Reference Neuffer1983) to hadrons (Poth Reference Poth1990), at the respective collider facilities. In these cases, emittance reflects the phase space necessary to decay and/or efficient production reactions, so transverse momentum is much larger, also exceeding the MeV/c range (Neuffer Reference Neuffer1983; Boscolo, Delahaye & Palmer Reference Boscolo, Delahaye and Palmer2019), with corresponding larger sizes (over 100 m). As for the unstable nuclei (also called ‘exotic’), in the example of the Selective Production of Exotic Species (SPES) (de Angelis et al. Reference de Angelis, Prete, Andrighetto, Manzolaro, Corradetti, Scarpa, Rossignoli, Monetti, Lollo and Calderolla2015) project at the Laboratori Nazionali di Legnaro (LNL), a H$^+$
(Neuffer Reference Neuffer1983) to hadrons (Poth Reference Poth1990), at the respective collider facilities. In these cases, emittance reflects the phase space necessary to decay and/or efficient production reactions, so transverse momentum is much larger, also exceeding the MeV/c range (Neuffer Reference Neuffer1983; Boscolo, Delahaye & Palmer Reference Boscolo, Delahaye and Palmer2019), with corresponding larger sizes (over 100 m). As for the unstable nuclei (also called ‘exotic’), in the example of the Selective Production of Exotic Species (SPES) (de Angelis et al. Reference de Angelis, Prete, Andrighetto, Manzolaro, Corradetti, Scarpa, Rossignoli, Monetti, Lollo and Calderolla2015) project at the Laboratori Nazionali di Legnaro (LNL), a H$^+$![]() beam from a cyclotron induces fission reactions in a hot target, with products first stopped into the target, then diffusing and singly ionized in an ion source (Manzolaro et al. Reference Manzolaro, Andrighetto, Meneghetti, Monetti, Scarpa, Rossignoli, Vasquez, Corradetti, Calderolla and Prete2014), labelled IS in figure 1(a).
beam from a cyclotron induces fission reactions in a hot target, with products first stopped into the target, then diffusing and singly ionized in an ion source (Manzolaro et al. Reference Manzolaro, Andrighetto, Meneghetti, Monetti, Scarpa, Rossignoli, Vasquez, Corradetti, Calderolla and Prete2014), labelled IS in figure 1(a).

Figure 1. Block diagrams (not to scale) of: (a) interdependence of the ion source IS, cooler RFQC and HRMS, as a zoom in the SPES project; (b) principle of RFQC confinement and cooling, with some electrodes, voltages and components shown; (c) the Eltrap machine RFQC installation, with emittance meter EMI1, ion source IS1 and Faraday cups FC1 and FC2.
This ion source has to cope with several technical complications (heat, radiation), limiting the source voltage $V_s \le 40$![]() kV. Most of all, the beam extracted from the source may contain many different ‘isobaric’ ions (for example $^{100}$
kV. Most of all, the beam extracted from the source may contain many different ‘isobaric’ ions (for example $^{100}$![]() Mo$^{1+}$
Mo$^{1+}$![]() and $^{100}$
and $^{100}$![]() Tc$^{1+}$
Tc$^{1+}$![]() ), which need to be separated before re-acceleration and delivery to experimental areas. In the SPES project, the envisioned high resolution mass spectrometer (HRMS) (de Angelis et al. Reference de Angelis, Prete, Andrighetto, Manzolaro, Corradetti, Scarpa, Rossignoli, Monetti, Lollo and Calderolla2015) has a resolution goal 1:20 000. The HRMS design therefore requests a high voltage platform (HVP) to increase the ion kinetic energy to $K_i \cong 160$
), which need to be separated before re-acceleration and delivery to experimental areas. In the SPES project, the envisioned high resolution mass spectrometer (HRMS) (de Angelis et al. Reference de Angelis, Prete, Andrighetto, Manzolaro, Corradetti, Scarpa, Rossignoli, Monetti, Lollo and Calderolla2015) has a resolution goal 1:20 000. The HRMS design therefore requests a high voltage platform (HVP) to increase the ion kinetic energy to $K_i \cong 160$![]() keV, and a normalized r.m.s. emittance $\epsilon ^N_x \le 2 \times 10^{-9}$
keV, and a normalized r.m.s. emittance $\epsilon ^N_x \le 2 \times 10^{-9}$![]() m (see definition later) with an energy spread $\sigma _E^o \le 1.5$
m (see definition later) with an energy spread $\sigma _E^o \le 1.5$![]() eVr.m.s., to be provided by the RFQC ion cooler inserted between IS and HVP (Bisoffi et al. Reference Bisoffi, Prete, Andrighetto, Andreev, Bellan, Bellato, Bortolato, Calderolla, Canella and Comunian2016; Comunian et al. Reference Comunian, Andrighetto, Antonini, Baltador, Bellan, Benini, Bermudez, Bisoffi, Bortolato and Calderolla2020).
eVr.m.s., to be provided by the RFQC ion cooler inserted between IS and HVP (Bisoffi et al. Reference Bisoffi, Prete, Andrighetto, Andreev, Bellan, Bellato, Bortolato, Calderolla, Canella and Comunian2016; Comunian et al. Reference Comunian, Andrighetto, Antonini, Baltador, Bellan, Benini, Bermudez, Bisoffi, Bortolato and Calderolla2020).
With some exceptions, such as stochastic cooling or synchrotron radiation (van der Meer Reference van der Meer1987; Möhl Reference Möhl1988), the cooling of particles $X$![]() (that is, the reduction of the momentum variance of this population) may be accomplished with two processes. The first is due to collisions where particles $X$
(that is, the reduction of the momentum variance of this population) may be accomplished with two processes. The first is due to collisions where particles $X$![]() exchange energy and momentum with a colder charged-particle beam (Poth Reference Poth1990) or a neutral gas. The other is a reacceleration, where all $X$
exchange energy and momentum with a colder charged-particle beam (Poth Reference Poth1990) or a neutral gas. The other is a reacceleration, where all $X$![]() particles receive an equal additional energy, from a radiofrequency (RF) cavity or a DC acceleration electrode structure. During these steps, particles $X$
particles receive an equal additional energy, from a radiofrequency (RF) cavity or a DC acceleration electrode structure. During these steps, particles $X$![]() must stay confined inside the cooler. To obtain these conditions (Neuffer Reference Neuffer1983), careful design, simulations and experimental verification of coolers are required.
must stay confined inside the cooler. To obtain these conditions (Neuffer Reference Neuffer1983), careful design, simulations and experimental verification of coolers are required.
In an RFQC (Boussaid et al. Reference Boussaid, Ban, Quéméner, Merrer and Lorry2017), which is a kind of linear ion trap, ions are decelerated and enter a gas cell, typically filled with helium at a pressure $p_g$![]() , which contains an RFQ with rods divided into $N$
, which contains an RFQ with rods divided into $N$![]() sections; ions are slowed down by this buffer gas and are confined by the RFQ voltages. By applying adequate drift voltages $V^s_i$
sections; ions are slowed down by this buffer gas and are confined by the RFQ voltages. By applying adequate drift voltages $V^s_i$![]() to the sections $i=1,\ldots,N$
to the sections $i=1,\ldots,N$![]() , ions are reaccelerated to the gas cell exit, where they are extracted. The final RFQC for SPES has $N=18$
, ions are reaccelerated to the gas cell exit, where they are extracted. The final RFQC for SPES has $N=18$![]() sections (Boussaid et al. Reference Boussaid, Ban, Quéméner, Merrer and Lorry2017). A first prototype of the SPES RFQC was designed by INFN-LNL, with only $N=10$
sections (Boussaid et al. Reference Boussaid, Ban, Quéméner, Merrer and Lorry2017). A first prototype of the SPES RFQC was designed by INFN-LNL, with only $N=10$![]() sections (Maggiore et al. Reference Maggiore, Cavenago, Comunian, Chiurlotto, Galatà, De Lazzari, Porcellato, Roncolato, Stark and Caruso2014), see figure 2. It is being adapted and installed into the Eltrap machine at Milan University (Amoretti et al. Reference Amoretti, Bettega, Cavaliere, Cavenago, De Luca, Pozzoli and Romé2003) to study the RFQC beam dynamics, see figure 1(b), the combined confinement effect of the RF and magnetic fields (Dholakia et al. Reference Dholakia, Horvath, Segal and Thompson1992; Li & Werth Reference Li and Werth1992; Beu, Hendrickson & Marshall Reference Beu, Hendrickson and Marshall2011; Cavenago et al. Reference Cavenago, Romé, Maero, Maggiore, Bellan, Cavaliere, Comunian, Galatà, Panzeri and Pisent2019) and the injection and extraction phases. In these tests, natural $^{133}$
sections (Maggiore et al. Reference Maggiore, Cavenago, Comunian, Chiurlotto, Galatà, De Lazzari, Porcellato, Roncolato, Stark and Caruso2014), see figure 2. It is being adapted and installed into the Eltrap machine at Milan University (Amoretti et al. Reference Amoretti, Bettega, Cavaliere, Cavenago, De Luca, Pozzoli and Romé2003) to study the RFQC beam dynamics, see figure 1(b), the combined confinement effect of the RF and magnetic fields (Dholakia et al. Reference Dholakia, Horvath, Segal and Thompson1992; Li & Werth Reference Li and Werth1992; Beu, Hendrickson & Marshall Reference Beu, Hendrickson and Marshall2011; Cavenago et al. Reference Cavenago, Romé, Maero, Maggiore, Bellan, Cavaliere, Comunian, Galatà, Panzeri and Pisent2019) and the injection and extraction phases. In these tests, natural $^{133}$![]() Cs$^{1+}$
Cs$^{1+}$![]() ions with a typical 100 nA current are provided by a commercial surface ionization ion source, IS1.
ions with a typical 100 nA current are provided by a commercial surface ionization ion source, IS1.

Figure 2. Side (a) and front (b) views of the RFQC prototype.
Multiple collisions with light gas molecules can cool a heavy ion, since the r.m.s. energy spread produced by each collision is (at most) of the order of the centre of mass energy $E_{{\rm cm}}$![]()
with $m_i$![]() the ion mass, $m_g$
the ion mass, $m_g$![]() the molecule mass and $\boldsymbol {v}$
the molecule mass and $\boldsymbol {v}$![]() the ion velocity; note that the gas thermal energy is negligible, at least for our application goals. To reduce $E_{{\rm cm}}$
the ion velocity; note that the gas thermal energy is negligible, at least for our application goals. To reduce $E_{{\rm cm}}$![]() we need to decelerate a beam to $K_i \cong 10$
we need to decelerate a beam to $K_i \cong 10$![]() eV, where the RF quadrupole focusing is one of the few effective focusing methods. After cooling, ions must be reaccelerated, avoiding focusing mismatches that will again heat the beam. Figure 1(b) sketches the damped motion inside the RFQC, and the Hamiltonian motion (no gas, no collisions) outside. This complex physics is worth detailed investigation in itself, to the extent possible in a dedicated test bench. Our test bench is the Eltrap machine (figure 1c), which also provides a static magnetic field $\boldsymbol {B}^s$
eV, where the RF quadrupole focusing is one of the few effective focusing methods. After cooling, ions must be reaccelerated, avoiding focusing mismatches that will again heat the beam. Figure 1(b) sketches the damped motion inside the RFQC, and the Hamiltonian motion (no gas, no collisions) outside. This complex physics is worth detailed investigation in itself, to the extent possible in a dedicated test bench. Our test bench is the Eltrap machine (figure 1c), which also provides a static magnetic field $\boldsymbol {B}^s$![]() for additional focusing.
for additional focusing.
In regard to general notations, let $xyz$![]() be the Eltrap reference frame with $z=0$
be the Eltrap reference frame with $z=0$![]() the middle plane of the solenoid, $z$
the middle plane of the solenoid, $z$![]() be the beamline axis and $s$
be the beamline axis and $s$![]() be the arc length of the central ion trajectory from the source exit plane at $z=z_s$
be the arc length of the central ion trajectory from the source exit plane at $z=z_s$![]() (by convention, $s=z_s-z$
(by convention, $s=z_s-z$![]() ). The magnetic field is aligned with the axis $z$
). The magnetic field is aligned with the axis $z$![]() within 0.2 mrad by the Eltrap design and correction coils.
within 0.2 mrad by the Eltrap design and correction coils.
The rest of the paper is organized as follows. In § 2, major features of the RFQC integration into the Eltrap machine are presented, including the gas pumping and the system of electrostatic lenses necessary for injection and extraction of the beam. In § 3, an updated theoretical approach, including the collisional scattering and cooling of the ions and their transport and manipulation by the applied fields, is summarized. Its implementation with a new tracing code is outlined and illustrated with simulation results, mostly corroborating the extraction tetrode design, as noted in the conclusion and perspective section.
2. General set-up
The RFQC insertion inside the Eltrap machine was described elsewhere; for example, see figure 1 of Cavenago et al. (Reference Cavenago, Romé, Maero, Maggiore, Bellan, Cavaliere, Comunian, Galatà, Panzeri and Pisent2019). The Eltrap machine features a high uniformity magnetic solenoid (1.5 m long) optimized for experiments with a Malmberg–Penning trap (Amoretti et al. Reference Amoretti, Bettega, Cavaliere, Cavenago, De Luca, Pozzoli and Romé2003); this trap has been used over the last 20 years to perform experiments on the dynamics of an electron plasma (Maero et al. Reference Maero, Pozzoli, Romé, Chen and Ikram2016). For the current project, the RFQC electrode structure is installed in the solenoid magnet, replacing the former electrode set-up. Since the RFQC prototype (Maggiore et al. Reference Maggiore, Cavenago, Comunian, Chiurlotto, Galatà, De Lazzari, Porcellato, Roncolato, Stark and Caruso2014; Cavenago et al. Reference Cavenago, Baltador, Bellan, Comunian, Fagotti, Galatà, Maero, Maggiore, Pisent and Romé2022) is shorter than the Eltrap solenoid, an injection line, formed by drift tubes ($V_0$![]() , $V_2$
, $V_2$![]() and $V_4$
and $V_4$![]() ) and two einzel lenses (at voltages $V_1$
) and two einzel lenses (at voltages $V_1$![]() and $V_3$
and $V_3$![]() ) and a deceleration section, is placed inside the solenoid, which may provide $|\boldsymbol {B}^s|$
) and a deceleration section, is placed inside the solenoid, which may provide $|\boldsymbol {B}^s|$![]() up to 0.2 T. Unlike a typical accelerator set-up where the RFQC has to be placed on a positive HVP and beamlines are generally at ground, the RFQC electrode DC voltages are here within 100 V from ground potential, so that drift tubes and emittance meter EMI1 are usually held at a common negative voltage $V_0$
up to 0.2 T. Unlike a typical accelerator set-up where the RFQC has to be placed on a positive HVP and beamlines are generally at ground, the RFQC electrode DC voltages are here within 100 V from ground potential, so that drift tubes and emittance meter EMI1 are usually held at a common negative voltage $V_0$![]() . To set reference values, in examples here we use $V_0=-4.8$
. To set reference values, in examples here we use $V_0=-4.8$![]() kV and a suitable ion source to ground voltage $V_s= + 200$
kV and a suitable ion source to ground voltage $V_s= + 200$![]() V, so the ion kinetic energy is $K_i = 5$
V, so the ion kinetic energy is $K_i = 5$![]() keV at source output (which is the IS1 maximum specification).
keV at source output (which is the IS1 maximum specification).
A Faraday cup named FC1 can be inserted into the drift tube $V_4$![]() to measure the injected current $I_{i1}$
to measure the injected current $I_{i1}$![]() . Ions enter the RFQC from the injection line after a deceleration (electrodes $V_5$
. Ions enter the RFQC from the injection line after a deceleration (electrodes $V_5$![]() , $V_6$
, $V_6$![]() and $V_7$
and $V_7$![]() ); at RFQC exit, ions are re-accelerated by a dedicated electrode arrangement (at voltages $V_8$
); at RFQC exit, ions are re-accelerated by a dedicated electrode arrangement (at voltages $V_8$![]() , $V_9$
, $V_9$![]() , $V_{9b}$
, $V_{9b}$![]() and $V_{10}$
and $V_{10}$![]() ), see figure 3. The beam can be intercepted by a retractable pepper-pot emittance meter EMI1. When EMI1 is pulled out of the beamline, ions reach a second Faraday cup FC2, which measures the transmitted current $I_{i2}$
), see figure 3. The beam can be intercepted by a retractable pepper-pot emittance meter EMI1. When EMI1 is pulled out of the beamline, ions reach a second Faraday cup FC2, which measures the transmitted current $I_{i2}$![]() ; we aim for an efficiency $I_{i2}/I_{i1} > 0.7$
; we aim for an efficiency $I_{i2}/I_{i1} > 0.7$![]() .
.

Figure 3. The RFQC conceptual reference scheme; some components (R1, R2, C1, C1s) of the RF multiplexer are labelled.
A box encloses the RFQC to maintain the gas pressure $p_g$![]() necessary for cooling. The extraction line (Cavenago et al. Reference Cavenago, Romé, Maero, Maggiore, Bellan, Cavaliere, Comunian, Galatà, Panzeri and Pisent2019) is actually cantilevered on this RFQC box, which lies on a 2 m girder (or support bar), where the injection line also sits; the girder is rigidly connected to a CF250 flange, forming a so-called ‘plugin’ module.
necessary for cooling. The extraction line (Cavenago et al. Reference Cavenago, Romé, Maero, Maggiore, Bellan, Cavaliere, Comunian, Galatà, Panzeri and Pisent2019) is actually cantilevered on this RFQC box, which lies on a 2 m girder (or support bar), where the injection line also sits; the girder is rigidly connected to a CF250 flange, forming a so-called ‘plugin’ module.
A matching box (placed in air, near CF250 flange) splits the 50 ohm output of a standard RF generator into two signals $V_{{\rm rf}1}$![]() and $V_{{\rm rf}2}$
and $V_{{\rm rf}2}$![]() (in phase opposition), assuming a $0.4$
(in phase opposition), assuming a $0.4$![]() nF load at 4 MHz. An in-vacuum multiplexer (a network of capacitors and resistances, see figure 3) connects the 40 electrodes of the RFQC to the signals $V_{{\rm rf}1}=-V_{{\rm rf}2}$
nF load at 4 MHz. An in-vacuum multiplexer (a network of capacitors and resistances, see figure 3) connects the 40 electrodes of the RFQC to the signals $V_{{\rm rf}1}=-V_{{\rm rf}2}$![]() and to the ten $V_i^s$
and to the ten $V_i^s$![]() bias voltages, which can be independently adjusted. In the example here we set $V_i^s=(-i+11)*10$
bias voltages, which can be independently adjusted. In the example here we set $V_i^s=(-i+11)*10$![]() V with respect to the RFQC box; with this choice for the first experiments, at RFQC input we have $K_i = e (V_s - V_1^s)\cong 100$
V with respect to the RFQC box; with this choice for the first experiments, at RFQC input we have $K_i = e (V_s - V_1^s)\cong 100$![]() eV, so that a 5 eVr.m.s. energy spread can be easily injected. Other choices can be tested later.
eV, so that a 5 eVr.m.s. energy spread can be easily injected. Other choices can be tested later.
The RF multiplexer, its connections and most of the other electrode connections are firmly supported on the plugin girder and/or the RFQC, see figure 4, as necessary for system reliability. Plugin also provides support for the movement of the Faraday cup FC1.

Figure 4. (a) Detail of the RF multiplexer (gas tight RFQC cover removed); the resistors are sandwiched between mica foils for heat disposal towards a large copper bar; capacitors C6 and C6s stay in the He gas region; (b) the plugin flange, seen from the vacuum side (before final vacuum-grade cleaning), with one CF40 flange RF input and twelve CF16 flanges for other connections (as partly labelled); the ion beam enters from the drift tube $V_0$![]() connected to the ion source IS1 and is isolated from the plugin flange.
connected to the ion source IS1 and is isolated from the plugin flange.
2.1. The differential gas pumping
Outside the RFQC box, in the rest of the vacuum chamber we aim at a pressure of $p_v \ll 0.01$![]() Pa, to be maintained with some care: injection and extraction lines communicate with the RFQC box by means of two antechambers, differentially pumped (through some tubes), see figure 5. Two other tubes connect the RFQC box to a He mass-flow controller and to a pressure gauge, both placed outside the solenoid. The differential gas pumping is an important part of the Eltrap RFQC set-up as well as of other installations, since gas collisions outside the RFQC may provoke large beam diffusion, as the ion speed is greater and confinement is not uniform there; this effect was also noted in SIMION (Manura & Dahl Reference Manura and Dahl2011) simulations of the RFQC for the SPES project. The gas pressure $p_g$
Pa, to be maintained with some care: injection and extraction lines communicate with the RFQC box by means of two antechambers, differentially pumped (through some tubes), see figure 5. Two other tubes connect the RFQC box to a He mass-flow controller and to a pressure gauge, both placed outside the solenoid. The differential gas pumping is an important part of the Eltrap RFQC set-up as well as of other installations, since gas collisions outside the RFQC may provoke large beam diffusion, as the ion speed is greater and confinement is not uniform there; this effect was also noted in SIMION (Manura & Dahl Reference Manura and Dahl2011) simulations of the RFQC for the SPES project. The gas pressure $p_g$![]() inside the RFQC has been scanned from 2 to 9 Pa in the following simulations, since the relatively large reacceleration voltage step (as mentioned before, 10 V after each section $i$
inside the RFQC has been scanned from 2 to 9 Pa in the following simulations, since the relatively large reacceleration voltage step (as mentioned before, 10 V after each section $i$![]() in the first planned experiments) may require more gas for ion cooling. To reduce gas leakage, the RFQC box should be fully closed, except for the iris-shaped low-voltage electrodes $V_7$
in the first planned experiments) may require more gas for ion cooling. To reduce gas leakage, the RFQC box should be fully closed, except for the iris-shaped low-voltage electrodes $V_7$![]() and $V_8$
and $V_8$![]() that close the ends of this box. The 2 mm radius of the iris pupil (or aperture), allowing for the ion passage, can be further reduced by optional macor collimators (with advantages for the pump operation but the disadvantage of a possible accumulation of surface charge). The gas injected into the RFQC box is regulated by the mass-flow controller, in feedback with the vacuum gauge; the gas escaping from the RFQC input and output pupils is intercepted by two antechambers, directly connected to the main turbopump (nominal pumping speed approximately 550 litre s$^{-1}$
that close the ends of this box. The 2 mm radius of the iris pupil (or aperture), allowing for the ion passage, can be further reduced by optional macor collimators (with advantages for the pump operation but the disadvantage of a possible accumulation of surface charge). The gas injected into the RFQC box is regulated by the mass-flow controller, in feedback with the vacuum gauge; the gas escaping from the RFQC input and output pupils is intercepted by two antechambers, directly connected to the main turbopump (nominal pumping speed approximately 550 litre s$^{-1}$![]() for nitrogen or helium) by a network of pipes.
for nitrogen or helium) by a network of pipes.

Figure 5. (a) View of gas pipes and septum inside the fourway cross, with triode electrodes V9 and V10 dismounted from antechamber A2 to show V8. (b) Overview of the emittance meter EMI1 port, gas pipes and related turbopumps.
The gas escaping from these antechambers to the main Eltrap vacuum is pumped by another turbopump (nominal pumping speed 330 litre s$^{-1}$![]() for nitrogen), see figure 5. The typical helium conductances of the gas pipes are approximately 3 litre s$^{-1}$
for nitrogen), see figure 5. The typical helium conductances of the gas pipes are approximately 3 litre s$^{-1}$![]() (longer one) and 7 litre s$^{-1}$
(longer one) and 7 litre s$^{-1}$![]() (shorter one); for each iris electrode V7 and V8, assuming a 1.5 mm radius, 15 mm long collimator (best case), we get a 0.6 litre s$^{-1}$
(shorter one); for each iris electrode V7 and V8, assuming a 1.5 mm radius, 15 mm long collimator (best case), we get a 0.6 litre s$^{-1}$![]() conductance (Livesey Reference Livesey1998). Thus antechambers A1 and A2 may reduce significantly gas leak to the main chamber, whose conductance to pumps may be estimated to be of 1 m$^3$
conductance (Livesey Reference Livesey1998). Thus antechambers A1 and A2 may reduce significantly gas leak to the main chamber, whose conductance to pumps may be estimated to be of 1 m$^3$![]() s$^{-1}$
s$^{-1}$![]() order (adequate for the installed pumps). The total gas leak flow $F_L \le 0.011$
order (adequate for the installed pumps). The total gas leak flow $F_L \le 0.011$![]() Pa m$^3$
Pa m$^3$![]() s$^{-1}$
s$^{-1}$![]() is safely lower than the one already demonstrated for SPES case, approximately 0.05 Pa m$^3$
is safely lower than the one already demonstrated for SPES case, approximately 0.05 Pa m$^3$![]() s$^{-1}$
s$^{-1}$![]() (Ruzzon et al. Reference Ruzzon, Maggiore, Gelain, Marcato, Ban, Bougard, Cam, Desrues, Gautier and Lory2023), but of course experimental tests of the Eltrap pumping system need to be done soon. In the RFQC installation, PEEK (polyether ether ketone) insulators are tolerated, taking into account the background gas diffused by the RFQC; this choice significantly mitigated costs. Operation experience of this challenging differential pumping and gas control system will be valuable for the design of similar RFQCs.
(Ruzzon et al. Reference Ruzzon, Maggiore, Gelain, Marcato, Ban, Bougard, Cam, Desrues, Gautier and Lory2023), but of course experimental tests of the Eltrap pumping system need to be done soon. In the RFQC installation, PEEK (polyether ether ketone) insulators are tolerated, taking into account the background gas diffused by the RFQC; this choice significantly mitigated costs. Operation experience of this challenging differential pumping and gas control system will be valuable for the design of similar RFQCs.
2.2. Extraction optics design
The current extraction system installed uses three electrodes (the so-called triode design), but more adjustable parameters are offered by a four electrode system (the so-called tetrode design), with voltages here labelled $V_8$![]() , $V_9$
, $V_9$![]() , $V_{9b}$
, $V_{9b}$![]() and $V_{10}$
and $V_{10}$![]() . Note that end positions and end voltages $V_8$
. Note that end positions and end voltages $V_8$![]() and $V_{10}$
and $V_{10}$![]() are typically fixed (or constrained within limited ranges) by the overall set-up and the specified final ion energy; for example here $V_{10}=-4.8$
are typically fixed (or constrained within limited ranges) by the overall set-up and the specified final ion energy; for example here $V_{10}=-4.8$![]() kV. Therefore, while a triode has only one fully adjustable voltage, a tetrode has two free voltages and the following analysis has also the goal to clarify whether this larger freedom is worth the additional complexity of more electrodes, in the challenging beam dynamics induced by the RFQC.
kV. Therefore, while a triode has only one fully adjustable voltage, a tetrode has two free voltages and the following analysis has also the goal to clarify whether this larger freedom is worth the additional complexity of more electrodes, in the challenging beam dynamics induced by the RFQC.
As shown in figure 6, tetrode geometry evolves from that of the triode by cutting the puller electrode into two parts divided about the middle plane $z=z_{9b}$![]() ; note also the electrode names and the location of the A2 antechamber cover at $z = -0.854$
; note also the electrode names and the location of the A2 antechamber cover at $z = -0.854$![]() m, which supports insulators (not shown) and electrodes. Excluding the RFQC rods and the input and output irises V7, V8, the electrodes have a cylindrical shape; some are tapered to accommodate the expansion of the beam. For the other acceleration gaps, take the middle of the lens gap as the reference lens plane; for our example, $z_8=-0.79$
m, which supports insulators (not shown) and electrodes. Excluding the RFQC rods and the input and output irises V7, V8, the electrodes have a cylindrical shape; some are tapered to accommodate the expansion of the beam. For the other acceleration gaps, take the middle of the lens gap as the reference lens plane; for our example, $z_8=-0.79$![]() m, $z_9=-0.8$
m, $z_9=-0.8$![]() m and $z_{10}=-0.91$
m and $z_{10}=-0.91$![]() m. Usually the beam electrode $V_{10}$
m. Usually the beam electrode $V_{10}$![]() and the emittance meter EMI1 are approximately at the same potential, with a null or weak lens between them; so we ignore their middle plane, and choose a plane at EMI1 input as the output or observation plane $z_o=-1.03$
and the emittance meter EMI1 are approximately at the same potential, with a null or weak lens between them; so we ignore their middle plane, and choose a plane at EMI1 input as the output or observation plane $z_o=-1.03$![]() m. Other RFQCs may use different electrode shapes, see figure 6(c).
m. Other RFQCs may use different electrode shapes, see figure 6(c).

Figure 6. Extraction systems: (a) triode and (b) tetrode design (radial $r$![]() coordinate enlarged as marked); (c) geometry (not to scale) using iris electrodes and larger gaps for higher voltages.
coordinate enlarged as marked); (c) geometry (not to scale) using iris electrodes and larger gaps for higher voltages.
3. Modelling concepts, simulations and results
A standard tool in beam transport simulations is the so-called ray tracing (precise calculation of single particle trajectories), which can resolve the rapid variations of ion speeds and DC fields (for example in the passage through the V8 pupil) with an adequately refined mesh (0.2 mm here) and time integrators. But ray tracing can treat only the friction force (Cavenago et al. Reference Cavenago, Romé, Maero, Maggiore, Bellan, Cavaliere, Comunian, Galatà, Panzeri and Pisent2019), and not the diffusion (or straggling) arising from collisions. The theoretical analysis presented in the following allows us to approximately describe the diffusion with the time evolution of its correlations, which can be added to the ray-tracing solver, obtaining a so-called ‘augmented solver’. This can model collisional cooling (or heating). On the other hand, the combined use of the so-called ‘macromotion’ concept (Moore et al. Reference Moore, Gianfrancesco, Lumbo and Schwarz2006; Schwarz Reference Schwarz2006) is still convenient.
Let $\omega = 2 {\rm \pi}f_1$![]() be the RF angular frequency, $\phi _s$
be the RF angular frequency, $\phi _s$![]() be the DC electric potential, $e$
be the DC electric potential, $e$![]() and $m_i$
and $m_i$![]() be the ion charge and mass and $m_g$
be the ion charge and mass and $m_g$![]() the gas molecule mass; $r_0$
the gas molecule mass; $r_0$![]() is the smaller distance between the RFQ electrode surfaces and the $z$
is the smaller distance between the RFQ electrode surfaces and the $z$![]() axis. In RFQCs, ion motion is approximately the sum (Moore et al. Reference Moore, Gianfrancesco, Lumbo and Schwarz2006; Schwarz Reference Schwarz2006) of a micromotion (at frequencies $f_1$
axis. In RFQCs, ion motion is approximately the sum (Moore et al. Reference Moore, Gianfrancesco, Lumbo and Schwarz2006; Schwarz Reference Schwarz2006) of a micromotion (at frequencies $f_1$![]() and harmonics) due to RF fields, and a macromotion (time averaged on a $1/f_1$
and harmonics) due to RF fields, and a macromotion (time averaged on a $1/f_1$![]() period), due to DC fields $\boldsymbol {E}^s$
period), due to DC fields $\boldsymbol {E}^s$![]() and $\boldsymbol {B}^s$
and $\boldsymbol {B}^s$![]() and to a ponderomotive potential $\phi _p$
and to a ponderomotive potential $\phi _p$![]() . For any RF electric field of the form $\Re \boldsymbol {E}^f(\boldsymbol {x})\,{\rm e}^{\mathrm {i} \omega t}$
. For any RF electric field of the form $\Re \boldsymbol {E}^f(\boldsymbol {x})\,{\rm e}^{\mathrm {i} \omega t}$![]() , we have $\phi _p= e |\boldsymbol {E}^f|^2/(4 m_i \omega ^2)$
, we have $\phi _p= e |\boldsymbol {E}^f|^2/(4 m_i \omega ^2)$![]() . Inside the RFQC, close to the $z$
. Inside the RFQC, close to the $z$![]() -axis this reduces to
-axis this reduces to
where $\varOmega _z$![]() is the ion cyclotron frequency, $V_{{\rm rf}}\cong V_{{\rm rf}1}$
is the ion cyclotron frequency, $V_{{\rm rf}}\cong V_{{\rm rf}1}$![]() is the amplitude of the applied RF voltage, $\omega _M$
is the amplitude of the applied RF voltage, $\omega _M$![]() is the so-called macromotion angular frequency and $k_q$
is the so-called macromotion angular frequency and $k_q$![]() is the Mathieu parameter: a sufficient condition for micromotion stability is $0< k_q<0.91+ O(\varOmega _z/\omega )^2$
is the Mathieu parameter: a sufficient condition for micromotion stability is $0< k_q<0.91+ O(\varOmega _z/\omega )^2$![]() .
.
We define the ponderomotive equivalent voltage $V_p \equiv \phi _p(r_0)$![]() . To make a first and gross statistical description of collisions, we neglect the micromotion from now on, so that $\boldsymbol {v}= {\rm d}_t \boldsymbol {x}$
. To make a first and gross statistical description of collisions, we neglect the micromotion from now on, so that $\boldsymbol {v}= {\rm d}_t \boldsymbol {x}$![]() is the velocity of the macromotion, with $\boldsymbol {x}$
is the velocity of the macromotion, with $\boldsymbol {x}$![]() the ion position averaged on a RF cycle. The macromotion is subjected to the ponderomotive potential $\phi _p$
the ion position averaged on a RF cycle. The macromotion is subjected to the ponderomotive potential $\phi _p$![]() , which has an approximate axial symmetry thanks to (3.1a–d), and to electrostatic and magnetostatic fields, which all have axial symmetry in our design; so the axial symmetry of the beam emitted by the source is approximately conserved in our beamline, neglecting misalignments. In the particular case of no collisions and no magnetic field at the ion source position $B_z(z_s)=0$
, which has an approximate axial symmetry thanks to (3.1a–d), and to electrostatic and magnetostatic fields, which all have axial symmetry in our design; so the axial symmetry of the beam emitted by the source is approximately conserved in our beamline, neglecting misalignments. In the particular case of no collisions and no magnetic field at the ion source position $B_z(z_s)=0$![]() , the radial displacement $r(z)$
, the radial displacement $r(z)$![]() satisfies the paraxial equation
satisfies the paraxial equation
close to the $z$![]() -axis, where $V(z)\equiv \phi _s(0,0,z_s)- \phi _s(0,0,z)$
-axis, where $V(z)\equiv \phi _s(0,0,z_s)- \phi _s(0,0,z)$![]() is called the accelerating potential; see chapter 6 and (4.25) for the beam rotation in Pierce (Reference Pierce1954). This shows the cooperation of $\omega _M$
is called the accelerating potential; see chapter 6 and (4.25) for the beam rotation in Pierce (Reference Pierce1954). This shows the cooperation of $\omega _M$![]() and $\varOmega _z$
and $\varOmega _z$![]() in confining the ions; also beam rotation is ${\rm d}_t \vartheta = \frac {1}{2} \varOmega _z$
in confining the ions; also beam rotation is ${\rm d}_t \vartheta = \frac {1}{2} \varOmega _z$![]() .
.
We now return to Cs$^+$![]() -He collisions. Many gas collisions are needed to change $\boldsymbol {v}$
-He collisions. Many gas collisions are needed to change $\boldsymbol {v}$![]() significantly, since $m_g/m_i = 0.03 \ll 1$
significantly, since $m_g/m_i = 0.03 \ll 1$![]() ; Langevin-style equations can model both the first $m_g/m_i$
; Langevin-style equations can model both the first $m_g/m_i$![]() order effect, which is a friction force $- \nu _m \boldsymbol {v}$
order effect, which is a friction force $- \nu _m \boldsymbol {v}$![]() , and the second-order straggling effect
, and the second-order straggling effect
where $\nu _m$![]() is the collision frequency, $\boldsymbol {E}^p=-\boldsymbol {\nabla } \phi _p$
is the collision frequency, $\boldsymbol {E}^p=-\boldsymbol {\nabla } \phi _p$![]() , $\boldsymbol {E}^s=-\boldsymbol {\nabla } \phi _s$
, $\boldsymbol {E}^s=-\boldsymbol {\nabla } \phi _s$![]() with $\phi _s$
with $\phi _s$![]() the DC potential, $\langle \rangle$
the DC potential, $\langle \rangle$![]() indicates the statistical average, $\boldsymbol \eta$
indicates the statistical average, $\boldsymbol \eta$![]() is a random kick, with its second-order moment given by the diffusion tensor $D$
is a random kick, with its second-order moment given by the diffusion tensor $D$![]() , and $k,n=1,2,3$
, and $k,n=1,2,3$![]() or $x,y,z$
or $x,y,z$![]() are coordinate indices. A preliminary study of the overall ion trajectories (from the source to the emittance meter EMI1) was given in Cavenago et al. (Reference Cavenago, Romé, Maero, Maggiore, Bellan, Cavaliere, Comunian, Galatà, Panzeri and Pisent2019) considering the friction force, but not straggling effects. Here, we approximately include straggling, that is, tensor $D$
are coordinate indices. A preliminary study of the overall ion trajectories (from the source to the emittance meter EMI1) was given in Cavenago et al. (Reference Cavenago, Romé, Maero, Maggiore, Bellan, Cavaliere, Comunian, Galatà, Panzeri and Pisent2019) considering the friction force, but not straggling effects. Here, we approximately include straggling, that is, tensor $D$![]() effects.
effects.
Indeed, an ion with given initial conditions $\boldsymbol {x}_0,\boldsymbol {v}_0$![]() at time $t=t_0$
at time $t=t_0$![]() follows a given trajectory $\boldsymbol {x}(t),\boldsymbol {v}(t)$
follows a given trajectory $\boldsymbol {x}(t),\boldsymbol {v}(t)$![]() , usually called a ray in accelerator beam optics, only in regions without gas, where $D=0$
, usually called a ray in accelerator beam optics, only in regions without gas, where $D=0$![]() . This trajectory can be calculated with so called ray-tracing methods, among which we have the leapfrog method and semi-implicit methods, including the so-called Boris rotation (Birdsall Reference Birdsall1985); a script using a matrix manipulation program (Matlab 2016) was written with both options. The concepts for including diffusion can be summarized as follows. As a result of the diffusion, $\boldsymbol {x}(t),\boldsymbol {v}(t)$
. This trajectory can be calculated with so called ray-tracing methods, among which we have the leapfrog method and semi-implicit methods, including the so-called Boris rotation (Birdsall Reference Birdsall1985); a script using a matrix manipulation program (Matlab 2016) was written with both options. The concepts for including diffusion can be summarized as follows. As a result of the diffusion, $\boldsymbol {x}(t),\boldsymbol {v}(t)$![]() become a distribution, whose averages can be computed; let us call ‘streamer’ or ‘ray pencil’ $P$
become a distribution, whose averages can be computed; let us call ‘streamer’ or ‘ray pencil’ $P$![]() the ensemble of diffused paths with a given initial condition $\boldsymbol {x}_0,\boldsymbol {v}_0$
the ensemble of diffused paths with a given initial condition $\boldsymbol {x}_0,\boldsymbol {v}_0$![]() . Let $\langle \rangle _P$
. Let $\langle \rangle _P$![]() be the average restricted to this ensemble $P$
be the average restricted to this ensemble $P$![]() ; similarly, let $R$
; similarly, let $R$![]() indicate the restriction to rays only. Define $\bar x = \langle x \rangle _P$
indicate the restriction to rays only. Define $\bar x = \langle x \rangle _P$![]() ; in a first approximation, $\bar x$
; in a first approximation, $\bar x$![]() can be computed with ray tracing as usual. Then $\tilde x = x - \bar x$
can be computed with ray tracing as usual. Then $\tilde x = x - \bar x$![]() is a random fluctuation around $\bar x$
is a random fluctuation around $\bar x$![]() ; define the second moments of this fluctuation as
; define the second moments of this fluctuation as
In paraxial approximation $v_x, v_y \ll |v_z|$![]() , and the $D$
, and the $D$![]() non-zero components are $D_{xx}=D_{yy}$
non-zero components are $D_{xx}=D_{yy}$![]() and $D_{zz}$
and $D_{zz}$![]() , calculated from interatomic potentials, in the same way as the mobility and collision frequencies (Schwarz Reference Schwarz2006; Cavenago et al. Reference Cavenago, Romé, Maero, Maggiore, Bellan, Cavaliere, Comunian, Galatà, Panzeri and Pisent2019). Calculating averages on the collision impact parameter as usual, we obtained $\nu _m = n_g f_1 |\boldsymbol {v}| \sigma _m$
, calculated from interatomic potentials, in the same way as the mobility and collision frequencies (Schwarz Reference Schwarz2006; Cavenago et al. Reference Cavenago, Romé, Maero, Maggiore, Bellan, Cavaliere, Comunian, Galatà, Panzeri and Pisent2019). Calculating averages on the collision impact parameter as usual, we obtained $\nu _m = n_g f_1 |\boldsymbol {v}| \sigma _m$![]() and for example the component $D_{xx}= n_g f_1^2 |\boldsymbol {v}|^3 \sigma _{xx}$
and for example the component $D_{xx}= n_g f_1^2 |\boldsymbol {v}|^3 \sigma _{xx}$![]() , with $\sigma _m$
, with $\sigma _m$![]() the momentum cross-section (McDaniel Reference McDaniel1973; Lieberman & Lichtenberg Reference Lieberman and Lichtenberg1994; Cavenago et al. Reference Cavenago, Baltador, Bellan, Comunian, Fagotti, Galatà, Maero, Maggiore, Pisent and Romé2022) and $\sigma _{xx}$
the momentum cross-section (McDaniel Reference McDaniel1973; Lieberman & Lichtenberg Reference Lieberman and Lichtenberg1994; Cavenago et al. Reference Cavenago, Baltador, Bellan, Comunian, Fagotti, Galatà, Maero, Maggiore, Pisent and Romé2022) and $\sigma _{xx}$![]() the transverse diffusion cross-section given in (5) of Cavenago et al. (Reference Cavenago, Baltador, Bellan, Comunian, Fagotti, Galatà, Maero, Maggiore, Pisent and Romé2022).
the transverse diffusion cross-section given in (5) of Cavenago et al. (Reference Cavenago, Baltador, Bellan, Comunian, Fagotti, Galatà, Maero, Maggiore, Pisent and Romé2022).
Time evolution of $a_{kn}$![]() , $b_{kn}$
, $b_{kn}$![]() , $c_{kn}$
, $c_{kn}$![]() follows from linearization of (3.3) around $\bar x$
follows from linearization of (3.3) around $\bar x$![]() , and axial symmetry in our case: the non-zero independent components are $a_{zz}$
, and axial symmetry in our case: the non-zero independent components are $a_{zz}$![]() , $b_{zz}$
, $b_{zz}$![]() , $c_{zz}$
, $c_{zz}$![]() , $a_{xx}=a_{yy}$
, $a_{xx}=a_{yy}$![]() , $b_{xx}=b_{yy}$
, $b_{xx}=b_{yy}$![]() and $c_{xx}=c_{yy}$
and $c_{xx}=c_{yy}$![]() as trivially expected, and also $c_{xy}=-c_{yx}$
as trivially expected, and also $c_{xy}=-c_{yx}$![]() due to the axial magnetic field (a total of 7 quantities out of 21 components). For $x,y$
due to the axial magnetic field (a total of 7 quantities out of 21 components). For $x,y$![]() we have
we have
with $\psi = e (\phi _s+\phi _p)/m_i$![]() ; notation $a_{,bc}$
; notation $a_{,bc}$![]() indicates the partial derivative of any quantity $a$
indicates the partial derivative of any quantity $a$![]() with respect to $b$
with respect to $b$![]() and $c$
and $c$![]() .
.
The so-called r.m.s. normalized emittance definition (Reiser & O-Shea Reference Reiser and O-Shea2008) can be generalized, considering axial symmetry and magnetic field, to
with $\boldsymbol {p}=(p_x,p_y,p_s)$![]() the ion mechanical momentum. This normalized emittance, its restriction $\epsilon _x^R$
the ion mechanical momentum. This normalized emittance, its restriction $\epsilon _x^R$![]() to averages only on the rays $\bar x$
to averages only on the rays $\bar x$![]() and its restriction $\epsilon _x^P$
and its restriction $\epsilon _x^P$![]() to fluctuations in a streamer $P$
to fluctuations in a streamer $P$![]() have remarkable properties and relations. The major result is that $\epsilon _x^P$
have remarkable properties and relations. The major result is that $\epsilon _x^P$![]() can be expressed by second-order average moments and satisfies a particularly simple time evolution law
can be expressed by second-order average moments and satisfies a particularly simple time evolution law
thanks to (3.6a,b) and (3.7a,b). Note that $D$![]() induces an emittance growth, while $\nu _m$
induces an emittance growth, while $\nu _m$![]() decreases the emittance, with an equilibrium value depending on the ion axial speed $|v_z|$
decreases the emittance, with an equilibrium value depending on the ion axial speed $|v_z|$![]() . Where gas is absent, $D_{xx}$
. Where gas is absent, $D_{xx}$![]() and $\nu _m$
and $\nu _m$![]() are zero, and $\epsilon _x^p$
are zero, and $\epsilon _x^p$![]() is constant; in gas cells, $\epsilon _x^p$
is constant; in gas cells, $\epsilon _x^p$![]() tends to the value $a_{xx} D_{xx}/\nu _m$
tends to the value $a_{xx} D_{xx}/\nu _m$![]() , which shows the need for good confinement (small $a_{xx}$
, which shows the need for good confinement (small $a_{xx}$![]() ) for good cooling. Typical $\epsilon _x^p$
) for good cooling. Typical $\epsilon _x^p$![]() values are approximately a few m$^2$
values are approximately a few m$^2$![]() s$^{-1}$
s$^{-1}$![]() , while $\epsilon _x^P$
, while $\epsilon _x^P$![]() , $\epsilon _x^R$
, $\epsilon _x^R$![]() and $\epsilon _x^N$
and $\epsilon _x^N$![]() , due to the division by the speed of light $c$
, due to the division by the speed of light $c$![]() included in standard definitions (Reiser & O-Shea Reference Reiser and O-Shea2008), have the dimension of a length and typical values of a few nanometres.
included in standard definitions (Reiser & O-Shea Reference Reiser and O-Shea2008), have the dimension of a length and typical values of a few nanometres.
3.1. Optical aberrations: the case of rapid re-acceleration after the RFQC
After the RFQC, ions are no longer subjected to collisions, but they suffer rapidly changing accelerations at lens planes, with distortions of beam optics known as ‘optical aberrations’ (El-Kareh & El-Kareh Reference El-Kareh and El-Kareh1970). To approximately model this localized feature, consider that $\phi _p$![]() is negligible outside the RFQC box, and the Bessel series expansion of the electrostatic potential $\phi _s$
is negligible outside the RFQC box, and the Bessel series expansion of the electrostatic potential $\phi _s$![]() close to the axis (El-Kareh & El-Kareh Reference El-Kareh and El-Kareh1970) then gives a similar expansion for
close to the axis (El-Kareh & El-Kareh Reference El-Kareh and El-Kareh1970) then gives a similar expansion for
with $\psi _0(z)$![]() the value of $\psi$
the value of $\psi$![]() on axis and $g(z)=-\psi _0''(z)/2$
on axis and $g(z)=-\psi _0''(z)/2$![]() a shorthand. This series converges only for $r$
a shorthand. This series converges only for $r$![]() smaller than the inner electrode radius, and $g(z)$
smaller than the inner electrode radius, and $g(z)$![]() has large oscillations at lens planes; $g''(z)$
has large oscillations at lens planes; $g''(z)$![]() has even greater oscillations. Let $v_0(z)=\sqrt {2(h-\psi _0(z))}$
has even greater oscillations. Let $v_0(z)=\sqrt {2(h-\psi _0(z))}$![]() be a reference speed, with $h=H/m_i$
be a reference speed, with $h=H/m_i$![]() and $H$
and $H$![]() the Hamiltonian, that is the total energy, which may be assumed for simplicity equal for all the ions. From the motion (3.3), with $s=z_s-z$
the Hamiltonian, that is the total energy, which may be assumed for simplicity equal for all the ions. From the motion (3.3), with $s=z_s-z$![]() , the $s$
, the $s$![]() -differential operator resolved as ${\rm d}_s = (1/|v_z|) {\rm d}_t$
-differential operator resolved as ${\rm d}_s = (1/|v_z|) {\rm d}_t$![]() , and $|v_z|$
, and $|v_z|$![]() calculated from energy conservation as shown in the Appendix, we get the evolution law
calculated from energy conservation as shown in the Appendix, we get the evolution law
where the leading term (with $g''$![]() and $g^2$
and $g^2$![]() ) is shown and $A_0$
) is shown and $A_0$![]() is a lengthy expression (see (A4)–(A6), containing similar terms, but without occurrences of $g''$
is a lengthy expression (see (A4)–(A6), containing similar terms, but without occurrences of $g''$![]() and $g^2$
and $g^2$![]() or higher powers; as introduced before, $s$
or higher powers; as introduced before, $s$![]() and $v_0$
and $v_0$![]() are respectively the arc length and the speed for the central ion trajectory. Since $g''(z)$
are respectively the arc length and the speed for the central ion trajectory. Since $g''(z)$![]() changes sign inside the lens, most changes are cancelled after exiting the lens, but some effects remain, and give an unwanted r.m.s. emittance growth at extraction (as shown by simulations).
changes sign inside the lens, most changes are cancelled after exiting the lens, but some effects remain, and give an unwanted r.m.s. emittance growth at extraction (as shown by simulations).
3.2. Simulation methods
For each ray, evolution equations (3.6a,b) and (3.7a,b) for the $\tilde {\boldsymbol {x}}, \tilde {\boldsymbol {v}}$![]() pencil second-order correlations are numerically solved in addition to the ray tracing. Note that $\psi _{,xx}$
pencil second-order correlations are numerically solved in addition to the ray tracing. Note that $\psi _{,xx}$![]() has large oscillations at the edges among RFQC sections and even larger oscillations at the middle planes $z_9$
has large oscillations at the edges among RFQC sections and even larger oscillations at the middle planes $z_9$![]() , $z_{9b}$
, $z_{9b}$![]() and $z_{10}$
and $z_{10}$![]() of the electrostatic lenses. The semi-implicit method proved much more stable than simple leapfrog, but it required a laborious development. The resulting script, called the augmented tracer (rays + streamers), can be advantageous for reasonably rapid and accurate calculation of electrode geometries (compared with a Monte Carlo requiring much more particle histories). The tracer also verifies that $\langle x^2 \rangle$
of the electrostatic lenses. The semi-implicit method proved much more stable than simple leapfrog, but it required a laborious development. The resulting script, called the augmented tracer (rays + streamers), can be advantageous for reasonably rapid and accurate calculation of electrode geometries (compared with a Monte Carlo requiring much more particle histories). The tracer also verifies that $\langle x^2 \rangle$![]() remains reasonably small ($\ll r_0$
remains reasonably small ($\ll r_0$![]() ) during the calculation, and implements the augmented semi-implicit methods, the leapfrog method and other user routines in a script for a general matrix program (Matlab 2016). The axisymmetric field maps of $\boldsymbol {B}^s$
) during the calculation, and implements the augmented semi-implicit methods, the leapfrog method and other user routines in a script for a general matrix program (Matlab 2016). The axisymmetric field maps of $\boldsymbol {B}^s$![]() and $\boldsymbol {E}^s$
and $\boldsymbol {E}^s$![]() , with mesh size refined to 0.2 mm where necessary, are imported from a multiphysics environment (Comsol 2008) and updated at any parameter change; an analytic formula is still used for $\phi _p$
, with mesh size refined to 0.2 mm where necessary, are imported from a multiphysics environment (Comsol 2008) and updated at any parameter change; an analytic formula is still used for $\phi _p$![]() . Evolution of the reduced averaged Hamiltonian $h=H/m_i= \frac {1}{2} \boldsymbol {v}^2 + \psi$
. Evolution of the reduced averaged Hamiltonian $h=H/m_i= \frac {1}{2} \boldsymbol {v}^2 + \psi$![]() and its fluctuation second momentum $b_{hh}= \langle (\tilde h)^2 \rangle$
and its fluctuation second momentum $b_{hh}= \langle (\tilde h)^2 \rangle$![]() are also computed by this ‘augmented’ tracer.
are also computed by this ‘augmented’ tracer.
3.3. Simulation results for triodes
Triode or tetrode extraction voltages $V_8$![]() , $V_9$
, $V_9$![]() and $V_{9b}$
and $V_{9b}$![]() can be adjusted for fast parametric scans, keeping $V_{10}=-4.8$
can be adjusted for fast parametric scans, keeping $V_{10}=-4.8$![]() kV fixed for reference (and to get the same kinetic energy); in the reported simulations we have $B_z=0.11$
kV fixed for reference (and to get the same kinetic energy); in the reported simulations we have $B_z=0.11$![]() T at solenoid centre; this gives a total beam rotation of approximately 8.5 rad. Note that the cases $V_9 \not = V_{9b}$
T at solenoid centre; this gives a total beam rotation of approximately 8.5 rad. Note that the cases $V_9 \not = V_{9b}$![]() do request a tetrode, while a tetrode with $V_9=V_{9b}$
do request a tetrode, while a tetrode with $V_9=V_{9b}$![]() is equivalent to a triode.
is equivalent to a triode.
Figure 7(a) shows emittance evolution for the whole beamline, at the good cooling rate obtained with $p_g=9$![]() Pa and a large ponderomotive equivalent voltage $V_p \equiv \phi _p(r_0)=3$
Pa and a large ponderomotive equivalent voltage $V_p \equiv \phi _p(r_0)=3$![]() V, with triode voltages set as $V_8=5$
V, with triode voltages set as $V_8=5$![]() V, $V_9=V_{9b}=-1.4$
V, $V_9=V_{9b}=-1.4$![]() kV and $V_{10}=-4.8$
kV and $V_{10}=-4.8$![]() kV. Case C2 refers to our test source IS1, which gives an initial normalized ray emittance $\varepsilon _x^R = 0.33$
kV. Case C2 refers to our test source IS1, which gives an initial normalized ray emittance $\varepsilon _x^R = 0.33$![]() nm. Case C1 doubles the initial beam radius and divergence, so emittance is $\varepsilon _x^R = 1.33$
nm. Case C1 doubles the initial beam radius and divergence, so emittance is $\varepsilon _x^R = 1.33$![]() nm at the source. Note that $\epsilon _x^R$
nm at the source. Note that $\epsilon _x^R$![]() is constant in the injection line and decreases smoothly to almost zero inside the RFQC; $\varepsilon _x^N$
is constant in the injection line and decreases smoothly to almost zero inside the RFQC; $\varepsilon _x^N$![]() is a combined effect of ray and streamer dynamics, since $\langle x^2 \rangle = \frac {1}{2} \langle x^2+y^2 + 2 a_{xx} \rangle _R$
is a combined effect of ray and streamer dynamics, since $\langle x^2 \rangle = \frac {1}{2} \langle x^2+y^2 + 2 a_{xx} \rangle _R$![]() . In both C1 and C2 cases, the values of $\varepsilon _x^N$
. In both C1 and C2 cases, the values of $\varepsilon _x^N$![]() at the RFQC exit converge to $\varepsilon _x^P$
at the RFQC exit converge to $\varepsilon _x^P$![]() , thus showing the importance of the ‘streamer’ dynamics. Another often used ‘geometrical emittance’ $\epsilon _x^g= (c/|v_z|) \epsilon _x^N$
, thus showing the importance of the ‘streamer’ dynamics. Another often used ‘geometrical emittance’ $\epsilon _x^g= (c/|v_z|) \epsilon _x^N$![]() is also plotted in figure 7, to highlight its typical changes during acceleration.
is also plotted in figure 7, to highlight its typical changes during acceleration.

Figure 7. Triode results for emittance evolution vs $z$![]() , with reference voltages $V_8=5$
, with reference voltages $V_8=5$![]() V, $V_{9b}=1.4$
V, $V_{9b}=1.4$![]() kV and $V_{10}=-4.8$
kV and $V_{10}=-4.8$![]() kV: (a) comparison at $p_g= 9$
kV: (a) comparison at $p_g= 9$![]() Pa and $V_p=3$
Pa and $V_p=3$![]() V of cases: C1, initial r.m.s. ray emittance $\epsilon _x^R = 1.33$
V of cases: C1, initial r.m.s. ray emittance $\epsilon _x^R = 1.33$![]() nm; C2, initial $\epsilon _x^R = 0.33$
nm; C2, initial $\epsilon _x^R = 0.33$![]() nm. The normalized total emittances $\epsilon _x^N$
nm. The normalized total emittances $\epsilon _x^N$![]() are slightly shifted up as labelled for visibility, and $\epsilon _x^g$
are slightly shifted up as labelled for visibility, and $\epsilon _x^g$![]() is scaled; (b) example of worst case simulations, multiplying $x,y$
is scaled; (b) example of worst case simulations, multiplying $x,y$![]() ion displacement by a $\mu _x=2$
ion displacement by a $\mu _x=2$![]() factor at restart plane $z_s=-0.73$
factor at restart plane $z_s=-0.73$![]() m, at low confinement $V_p=2$
m, at low confinement $V_p=2$![]() V and moderate gas pressure $p_g=6$
V and moderate gas pressure $p_g=6$![]() Pa.
Pa.
A beam with an emittance value up to $\epsilon _x^R=1.33 \times 10^{-9}$![]() m at the source (corresponding to an r.m.s. $\epsilon _x^g = 4.6 \times 10^{-6}$
m at the source (corresponding to an r.m.s. $\epsilon _x^g = 4.6 \times 10^{-6}$![]() m at $K_i=5$
m at $K_i=5$![]() keV) can thus be injected inside the prototype RFQC with the present injection line, safely matching the existing Cs$^+$
keV) can thus be injected inside the prototype RFQC with the present injection line, safely matching the existing Cs$^+$![]() source, which has a lower emittance $\epsilon _x^R=0.33$
source, which has a lower emittance $\epsilon _x^R=0.33$![]() nm. For comparison, the SPES plasma ion source r.m.s. geometrical emittances are approximately $\epsilon ^g_{x1} = \epsilon ^g_{y1} \le 7 \times 10^{-6}$
nm. For comparison, the SPES plasma ion source r.m.s. geometrical emittances are approximately $\epsilon ^g_{x1} = \epsilon ^g_{y1} \le 7 \times 10^{-6}$![]() m at an ion energy $K_i=25$
m at an ion energy $K_i=25$![]() keV, so that the r.m.s. normalized emittance is $\epsilon ^N_x = \beta \gamma \epsilon ^{g}_{x1} \cong 5 \times 10^{-9}$
keV, so that the r.m.s. normalized emittance is $\epsilon ^N_x = \beta \gamma \epsilon ^{g}_{x1} \cong 5 \times 10^{-9}$![]() m (requiring an RFQC larger than our prototype, or larger RF fields); its energy spread is expected to be of the order of 10 eVpp (Bisoffi et al. Reference Bisoffi, Prete, Andrighetto, Andreev, Bellan, Bellato, Bortolato, Calderolla, Canella and Comunian2016), satisfying the $\sigma _E^{{\rm in}} \cong 5$
m (requiring an RFQC larger than our prototype, or larger RF fields); its energy spread is expected to be of the order of 10 eVpp (Bisoffi et al. Reference Bisoffi, Prete, Andrighetto, Andreev, Bellan, Bellato, Bortolato, Calderolla, Canella and Comunian2016), satisfying the $\sigma _E^{{\rm in}} \cong 5$![]() eVr.m.s. goal.
eVr.m.s. goal.
As an option to further test the RFQC extraction, the tracer script can restart ‘magnified’ rays $\boldsymbol {x}_M$![]() at a given plane $z=z_r=-0.73$
at a given plane $z=z_r=-0.73$![]() m, multiplying transverse displacements and velocities by a safety factor $\mu _x$
m, multiplying transverse displacements and velocities by a safety factor $\mu _x$![]() , but conserving energy; namely, the new initial conditions are $x_M(z_r) = \mu _x x(z_r)$
, but conserving energy; namely, the new initial conditions are $x_M(z_r) = \mu _x x(z_r)$![]() , $y_M(z_r) = \mu _x y(z_r)$
, $y_M(z_r) = \mu _x y(z_r)$![]() and similarly for $v_x,v_y$
and similarly for $v_x,v_y$![]() . This roughly accounts for the fact that ray emittance $\epsilon _x^R$
. This roughly accounts for the fact that ray emittance $\epsilon _x^R$![]() damps to almost zero near the RFQC exit, but ions still have a transverse motion as shown by $\epsilon _x^P$
damps to almost zero near the RFQC exit, but ions still have a transverse motion as shown by $\epsilon _x^P$![]() (other resampling algorithms are in development).
(other resampling algorithms are in development).
Figure 7(b) considers a moderate gas pressure $p_g=6$![]() Pa and a relatively weak confinement $V_p=2$
Pa and a relatively weak confinement $V_p=2$![]() V, which corresponds to a relatively low RF amplitude $V_{{\rm rf}}= 209$
V, which corresponds to a relatively low RF amplitude $V_{{\rm rf}}= 209$![]() V and a safe $k_q= 0.03$
V and a safe $k_q= 0.03$![]() , at $f_1=4$
, at $f_1=4$![]() MHz. With $\mu _x =2$
MHz. With $\mu _x =2$![]() , figure 7(b) shows a large r.m.s. emittance peak near $z=z_{10}=-0.92$
, figure 7(b) shows a large r.m.s. emittance peak near $z=z_{10}=-0.92$![]() m.
m.
From the comparison of rays for the cases $\mu _1 =1$![]() (no change at the restart plane) and $\mu _1 =2$
(no change at the restart plane) and $\mu _1 =2$![]() , see figure 8, we see that the latter case shows $|x|\cong 4$
, see figure 8, we see that the latter case shows $|x|\cong 4$![]() mm at $z_{10}$
mm at $z_{10}$![]() , enhancing nonlinear effects or aberrations (as expected). Indeed $\epsilon _x^P$
, enhancing nonlinear effects or aberrations (as expected). Indeed $\epsilon _x^P$![]() , which is governed by the linearized (3.9a,b), does not show any peak in figure 7(b), while $\epsilon _x^N(z)$
, which is governed by the linearized (3.9a,b), does not show any peak in figure 7(b), while $\epsilon _x^N(z)$![]() and on a smaller scale $\epsilon _x^R(z)$
and on a smaller scale $\epsilon _x^R(z)$![]() do show peaks at $z_{10}$
do show peaks at $z_{10}$![]() , which is the last electrostatic lens at the border of $V_{10}$
, which is the last electrostatic lens at the border of $V_{10}$![]() and $V_{9b}$
and $V_{9b}$![]() (see figure 3), where we expect third-order aberrations (El-Kareh & El-Kareh Reference El-Kareh and El-Kareh1970), as discussed in § 3.1. Note also that the $\epsilon _x^P(z_o)$
(see figure 3), where we expect third-order aberrations (El-Kareh & El-Kareh Reference El-Kareh and El-Kareh1970), as discussed in § 3.1. Note also that the $\epsilon _x^P(z_o)$![]() attains a value of approximately 2.2 nm for this case ($p_g=6$
attains a value of approximately 2.2 nm for this case ($p_g=6$![]() Pa and $V_p=2$
Pa and $V_p=2$![]() V). In a phase space plot (not shown), the growth is due to the deformation, also known as warping or filamentation, of the area filled with ions. Some smoothing is then applied to $\epsilon _x^N(z)$
V). In a phase space plot (not shown), the growth is due to the deformation, also known as warping or filamentation, of the area filled with ions. Some smoothing is then applied to $\epsilon _x^N(z)$![]() , and plotted as a dashed line in figures 7(b) and 9, to enhance the visibility of permanent effects. These effects include an increase of the output radius $r_o$
, and plotted as a dashed line in figures 7(b) and 9, to enhance the visibility of permanent effects. These effects include an increase of the output radius $r_o$![]() and of the emittance $\epsilon _o=\epsilon _x^N(z_o)$
and of the emittance $\epsilon _o=\epsilon _x^N(z_o)$![]() at the output plane $z=z_o=-1.03$
at the output plane $z=z_o=-1.03$![]() m (input plane of the emittance meter EMI1).
m (input plane of the emittance meter EMI1).

Figure 8. Samples of output rays for the figure 7(b) triode: (a) ray tracing without safety factor at restarting, so $\mu _x=1$![]() ; (b) $\mu _x=2$
; (b) $\mu _x=2$![]() . Potential $\phi _s$
. Potential $\phi _s$![]() plot uses the right axis (R); inner, middle and outer rays are grouped by their starting positions. Only rays starting at $y=0$
plot uses the right axis (R); inner, middle and outer rays are grouped by their starting positions. Only rays starting at $y=0$![]() , $x>0$
, $x>0$![]() are plotted (for clarity); other ray contributions to figure 7(b) are recovered by axial symmetry.
are plotted (for clarity); other ray contributions to figure 7(b) are recovered by axial symmetry.

Figure 9. Tetrode result for emittances, for $p_g=6$![]() Pa, $V_p=2$
Pa, $V_p=2$![]() V, $V_8=5$
V, $V_8=5$![]() V, $V_9=-300$
V, $V_9=-300$![]() V, $V_{9b}=-1.4$
V, $V_{9b}=-1.4$![]() kV and $\mu _x=2$
kV and $\mu _x=2$![]() , using geometries: (a) first design (longer front puller); (b) second design (6 cm long front puller).
, using geometries: (a) first design (longer front puller); (b) second design (6 cm long front puller).
3.4. Triode and improved tetrode comparisons
In the triode system, the puller effective length $z_{10}-z_9\cong 0.11$![]() m is too large, yielding undesired beam expansion. A first example of a tetrode was designed and built with cut plane $z_{9b}=-0.88$
m is too large, yielding undesired beam expansion. A first example of a tetrode was designed and built with cut plane $z_{9b}=-0.88$![]() m, for the convenience of firmly supporting electrode $V_9$
m, for the convenience of firmly supporting electrode $V_9$![]() with an isolator simply bolted over the A2 cover. Simulations partly reported in figure 9 have shown two possible limitations of this design: the effective front puller length of 8 cm is still too large; the lens at $z_{9b}$
with an isolator simply bolted over the A2 cover. Simulations partly reported in figure 9 have shown two possible limitations of this design: the effective front puller length of 8 cm is still too large; the lens at $z_{9b}$![]() and $z_{10}$
and $z_{10}$![]() are not clearly separated; so appreciable emittance peaks are seen at $z_{9b}$
are not clearly separated; so appreciable emittance peaks are seen at $z_{9b}$![]() and $z_{10}$
and $z_{10}$![]() in figure 9(a). In the second tetrode design (to be built), $z_{9b}=-0.86$
in figure 9(a). In the second tetrode design (to be built), $z_{9b}=-0.86$![]() m so that the puller length of 5 cm becomes safely greater than its inner diameter $D_p=28$
m so that the puller length of 5 cm becomes safely greater than its inner diameter $D_p=28$![]() mm and the front puller length decreases down to 6 cm; so emittance peaks almost disappear in figure 9(b). The following results refer to this second design.
mm and the front puller length decreases down to 6 cm; so emittance peaks almost disappear in figure 9(b). The following results refer to this second design.
In figure 10 the dependence of $\epsilon _o$![]() on $V_8$
on $V_8$![]() and $V_9$
and $V_9$![]() is shown, for a constant $V_{9b}=-1.4$
is shown, for a constant $V_{9b}=-1.4$![]() kV which corresponds to the previously optimized value for the triode, with a simpler friction force and optics modelling (Cavenago et al. Reference Cavenago, Romé, Maero, Maggiore, Bellan, Cavaliere, Comunian, Galatà, Panzeri and Pisent2019). For the region $|V_9 /V_{9b} | \ll 1$
kV which corresponds to the previously optimized value for the triode, with a simpler friction force and optics modelling (Cavenago et al. Reference Cavenago, Romé, Maero, Maggiore, Bellan, Cavaliere, Comunian, Galatà, Panzeri and Pisent2019). For the region $|V_9 /V_{9b} | \ll 1$![]() , note the satisfying performance for $V_9 \cong -200 \pm 150$
, note the satisfying performance for $V_9 \cong -200 \pm 150$![]() V, without appreciable emittance growth; in this $V_9$
V, without appreciable emittance growth; in this $V_9$![]() range, for any $V_8$
range, for any $V_8$![]() shown, the total (r.m.s. normalized) emittance $\epsilon _x^N$
shown, the total (r.m.s. normalized) emittance $\epsilon _x^N$![]() values approach and coalesce to the pencil emittance value $\epsilon _x^P \cong 2.2$
values approach and coalesce to the pencil emittance value $\epsilon _x^P \cong 2.2$![]() nm for $p_g=6$
nm for $p_g=6$![]() Pa and $V_p=2$
Pa and $V_p=2$![]() V, as noted before. This value is due to gas collisions and RFQC trap properties, and thus represents a lower bound (present also with ideal extraction) for the total emittance.
V, as noted before. This value is due to gas collisions and RFQC trap properties, and thus represents a lower bound (present also with ideal extraction) for the total emittance.

Figure 10. Output maximum radius $r_o$![]() and r.m.s. normalized emittance $\epsilon _x^N(z_o)$
and r.m.s. normalized emittance $\epsilon _x^N(z_o)$![]() vs the front puller tetrode voltage $V_9$
vs the front puller tetrode voltage $V_9$![]() for several $V_8$
for several $V_8$![]() values, and other conditions as in figure 9.
values, and other conditions as in figure 9.
Taking into account that experiments will start with a triode system, figure 11(a) shows the dependence of $\epsilon _x^P$![]() on pressure $p_g$
on pressure $p_g$![]() ; since the total emittance includes pencil diffusion effects, the use of larger pressures and a larger ponderomotive voltage $V_p=3$
; since the total emittance includes pencil diffusion effects, the use of larger pressures and a larger ponderomotive voltage $V_p=3$![]() V is worthwhile. Energy spread cooling is easier, as shown by figure 11(b) with $\sigma _E^o \le 0.4$
V is worthwhile. Energy spread cooling is easier, as shown by figure 11(b) with $\sigma _E^o \le 0.4$![]() eVr.m.s. obtained for $p_g>3$
eVr.m.s. obtained for $p_g>3$![]() Pa. Moreover, as long as $p_g=9$
Pa. Moreover, as long as $p_g=9$![]() Pa can be sustained by pumping system, acceptable final emittance $\epsilon _x^N$
Pa can be sustained by pumping system, acceptable final emittance $\epsilon _x^N$![]() are obtained in figure 7(a).
are obtained in figure 7(a).

Figure 11. Pressure and triode voltage scans: (a) comparison of pencil emittance $\epsilon _x^P$![]() for $V_p=3$
for $V_p=3$![]() V and initial $\epsilon _x^R = 0.33$
V and initial $\epsilon _x^R = 0.33$![]() nm at several $p_g$
nm at several $p_g$![]() ; (b) output energy spread for initial $\sigma _E^{{\rm in}}=5$
; (b) output energy spread for initial $\sigma _E^{{\rm in}}=5$![]() rVms and $V_p=3$
rVms and $V_p=3$![]() V and several $p_g$
V and several $p_g$![]() , $V_{9b}$
, $V_{9b}$![]() ; some contour levels are labelled with arrows.
; some contour levels are labelled with arrows.
When $p_g \le 6$![]() Pa, the triode performance can be improved by biasing the RFQC box exit pupil $V_8$
Pa, the triode performance can be improved by biasing the RFQC box exit pupil $V_8$![]() (reference design value $V_8=5$
(reference design value $V_8=5$![]() V) to negative voltages as $V_8=-30$
V) to negative voltages as $V_8=-30$![]() V, to pre-accelerate the extracted ions, as shown by $V_9=-1.4$
V, to pre-accelerate the extracted ions, as shown by $V_9=-1.4$![]() kV points in figure 10. When a compact tetrode with a $|z_{9b}-z_9|\le 6$
kV points in figure 10. When a compact tetrode with a $|z_{9b}-z_9|\le 6$![]() cm front puller length is used, figure 9(b) shows that the emittance growth can be suppressed also at the nominal reference voltage $V_8=5$
cm front puller length is used, figure 9(b) shows that the emittance growth can be suppressed also at the nominal reference voltage $V_8=5$![]() V. The promising option of changing bias voltages $V_i^s$
V. The promising option of changing bias voltages $V_i^s$![]() to reduce the ion speed in the RFQC and then $p_g$
to reduce the ion speed in the RFQC and then $p_g$![]() by a large amount certainly deserves future study, but requires a consolidation of the $\sigma _E^{{\rm in}}$
by a large amount certainly deserves future study, but requires a consolidation of the $\sigma _E^{{\rm in}}$![]() requirements.
requirements.
4. Discussion, conclusion and perspectives
In conclusion, emittance and energy spread trends can be computed at the end of the RFQC for several gas pressures $p_g$![]() , as shown in figures 11(a) and 11(b), thanks to the inclusion of diffusion effects of collisions in the equations of motion and in related computational tracers, as shown above. The normalized r.m.s. emittance $\epsilon _x^N$
, as shown in figures 11(a) and 11(b), thanks to the inclusion of diffusion effects of collisions in the equations of motion and in related computational tracers, as shown above. The normalized r.m.s. emittance $\epsilon _x^N$![]() may grow in the RFQC extraction with a triode electrode set-up as shown in figure 7(b), but this problem can be solved with a tetrode set-up, see figure 9(b).
may grow in the RFQC extraction with a triode electrode set-up as shown in figure 7(b), but this problem can be solved with a tetrode set-up, see figure 9(b).
The advantage of a tetrode configuration comes from its capability to reduce the first reacceleration of the beam and the consequent over-focusing at the RFQC exit pupil; otherwise, the beam will diverge rapidly after its focus, reaching a larger radius near the last lens plane $z_{10}$![]() , with an enhancement of the $g'' r^2$
, with an enhancement of the $g'' r^2$![]() aberration.
aberration.
To only envision other systems, we would have to consider space charge (Pierce Reference Pierce1954) as a method to reduce this over-focusing; since the current of the exotic ion beam is very small, a second ion beam should be injected in the system, which opens the issues of colliding ion systems; also its feasibility is not obvious.
We conclude that the tetrode appears to be an appealing solution, which anyway depends on the mechanical achievable spacing between the $z_8$![]() and $z_9$
and $z_9$![]() planes, so that construction and test of a few variants is highly recommended. Larger magnetic fields at extraction, and/or RFQ fields (Boussaid et al. Reference Boussaid, Ban, Quéméner, Merrer and Lorry2017), are worth investigation, also in comparison with other RFQCs.
planes, so that construction and test of a few variants is highly recommended. Larger magnetic fields at extraction, and/or RFQ fields (Boussaid et al. Reference Boussaid, Ban, Quéméner, Merrer and Lorry2017), are worth investigation, also in comparison with other RFQCs.
Acknowledgements
Work partly supported by INFN-CSN5 (Commissione Scientifica Nazionale 5: Ricerche Tecnologiche-Technological Researches) as part of the experimental activity Ion2neutral.
Editor Francesco Califano Special Collection: Non-Neutral Plasmas: Achievements and Perspectives thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Extraction optics nonlinear effects in $r$ power series
power series
Expanding the Hamiltonian $h=H/m_i= \frac {1}{2} \boldsymbol {v}^2 + (e /m_i) (\phi _s+\phi _p)$![]() in powers of $r$
in powers of $r$![]() as
as
and using the definition of $v_0$![]() , considering $g r^2$
, considering $g r^2$![]() and $v_x^2$
and $v_x^2$![]() of the same formal order, the inverse axial speed can be written as
of the same formal order, the inverse axial speed can be written as

with $n$![]() and $n_0$
and $n_0$![]() shorthands. The expression of ${\rm d}_s (\epsilon_x^R)^2$
shorthands. The expression of ${\rm d}_s (\epsilon_x^R)^2$![]() is a sum of terms such as
is a sum of terms such as
Inserting in these terms (A2a–c) for the axial speed and the equations of motion for ${\rm d}_t v_x$![]() with the expansion of (3.10a,b) for $E_x$
with the expansion of (3.10a,b) for $E_x$![]() and $E_y$
and $E_y$![]() , neglecting $\varOmega _z(z)$
, neglecting $\varOmega _z(z)$![]() slow changes and finally collecting all terms in ${\rm d}_s (\epsilon_x^R)^2$
slow changes and finally collecting all terms in ${\rm d}_s (\epsilon_x^R)^2$![]() , we can arrange the leading terms as shown in (3.11), and the remaining terms are
, we can arrange the leading terms as shown in (3.11), and the remaining terms are
Terms (A5) are suppressed for round beam symmetry.
These considerations apply also to SPES RFQC extraction, where electrodes corresponding to $V_9$![]() and $V_{9b}$
and $V_{9b}$![]() have a different shape (iris-shaped disks) to accommodate holding of larger voltages, and the beam electrode has a front collimator, see figure 6(c). Comparative simulations are in progress. To reduce the operating pressure $p_g$
have a different shape (iris-shaped disks) to accommodate holding of larger voltages, and the beam electrode has a front collimator, see figure 6(c). Comparative simulations are in progress. To reduce the operating pressure $p_g$![]() , the ion speed inside RFQC is designed to be smaller and thus more accurate voltage power supplies are required (than in Eltrap). The larger space available in the SPES beamline allows us to use electrostatic triplets (instead of einzel lenses) for a more gradual focusing.
, the ion speed inside RFQC is designed to be smaller and thus more accurate voltage power supplies are required (than in Eltrap). The larger space available in the SPES beamline allows us to use electrostatic triplets (instead of einzel lenses) for a more gradual focusing.