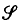§1. Introduction. Let X be a Hausdorff space and let ρ be a metric, not necessarily related to the topology of X. The space X is said to be fragmented by the metric ρ if each non-empty set in X has non-empty relatively open subsets of arbitrarily small ρ-diameter. The space X is said to be a σ-fragmented by the metric ρ if, for each ε>0, it is possible to write

where each set Xi, i≥1, has the property that each non-empty subset of Xi, has a non-empty relatively open subset of ρ-diameter less than ε. If 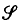 is any family of subsets of X, we say that X is σ-fragmented by the metric ρ, using sets from
is any family of subsets of X, we say that X is σ-fragmented by the metric ρ, using sets from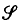 , if, for each ε>0, the sets Xi, i ≥ 1, in (1.1) can be taken from
, if, for each ε>0, the sets Xi, i ≥ 1, in (1.1) can be taken from