Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
NAMIOKA, I.
1994.
s̀‐Fragmented Banach Spaces and Function Spaces.
Annals of the New York Academy of Sciences,
Vol. 728,
Issue. 1,
p.
324.
Namioka, I.
and
Pol, R.
1996.
σ‐fragmentability and analyticity.
Mathematika,
Vol. 43,
Issue. 1,
p.
172.
Moors, W. B.
and
Giles, J. R.
1997.
Generic continuity of minimal set-valued mappings.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 63,
Issue. 2,
p.
238.
Bouziad, Ahmed
1997.
A quasi-closure preserving sum theorem about the Namioka property.
Topology and its Applications,
Vol. 81,
Issue. 2,
p.
163.
Namioka, Isaac
and
Pol, Roman
1998.
Sigma-fragmentability of mappings into Cp(K).
Topology and its Applications,
Vol. 89,
Issue. 3,
p.
249.
Mirmostafaee, A. K.
1998.
On non-fragmentability of Banach spaces.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 108,
Issue. 2,
p.
163.
Ribarska, Nadezhda K.
1998.
Three space property for σ‐fragmentability.
Mathematika,
Vol. 45,
Issue. 1,
p.
113.
Arhangel'skii, A.V.
1998.
Some observations on Cp-theory and bibliography.
Topology and its Applications,
Vol. 89,
Issue. 3,
p.
203.
Jayne, J. E.
Namioka, I.
and
Rogers, C. A.
1999.
Continuous functions on products of compact Hausdorff spaces.
Mathematika,
Vol. 46,
Issue. 2,
p.
323.
Raja, M.
1999.
Locally uniformly rotund norms.
Mathematika,
Vol. 46,
Issue. 2,
p.
343.
Moltó, A
Orihuela, J
Troyanski, S
and
Valdivia, M
1999.
On Weakly Locally Uniformly Rotund Banach Spaces.
Journal of Functional Analysis,
Vol. 163,
Issue. 2,
p.
252.
Bandyopadhyay, P
Huang, Da
Lin, Bor-Luh
and
Troyanski, S.L
2000.
Some Generalizations of Locally Uniform Rotundity.
Journal of Mathematical Analysis and Applications,
Vol. 252,
Issue. 2,
p.
906.
2001.
Encyclopaedia of Mathematics, Supplement III.
p.
274.
Kenderov, P.S.
Kortezov, I.S.
and
Moors, W.B.
2001.
Continuity points of quasi-continuous mappings.
Topology and its Applications,
Vol. 109,
Issue. 3,
p.
321.
Hansell, Roger W.
2001.
Absolute Souslin-F spaces and other weak-invariants of the norm topology.
Topology and its Applications,
Vol. 111,
Issue. 1-2,
p.
151.
Moors, Warren B.
and
Sciffer, Scott
2002.
Sigma-fragmentable spaces that are not countable unions of fragmentable subspaces.
Topology and its Applications,
Vol. 119,
Issue. 3,
p.
279.
Raja, M.
2002.
On dual locally uniformly rotund norms.
Israel Journal of Mathematics,
Vol. 129,
Issue. 1,
p.
77.
Zizler, Václav
2003.
Vol. 2,
Issue. ,
p.
1743.
Kenderov, Petar S.
and
Moors, Warren B.
2004.
A dual differentiation space without an equivalent locally uniformly rotund norm.
Journal of the Australian Mathematical Society,
Vol. 77,
Issue. 3,
p.
357.
Mirmostafaee, A. K.
2005.
A note on convex renorming and fragmentability.
Proceedings Mathematical Sciences,
Vol. 115,
Issue. 2,
p.
201.

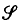 is any family of subsets of X, we say that X is σ-fragmented by the metric ρ, using sets from
is any family of subsets of X, we say that X is σ-fragmented by the metric ρ, using sets from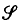 , if, for each ε>0, the sets Xi, i ≥ 1, in (1.1) can be taken from
, if, for each ε>0, the sets Xi, i ≥ 1, in (1.1) can be taken from