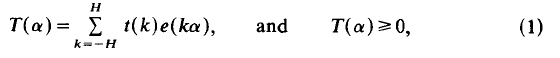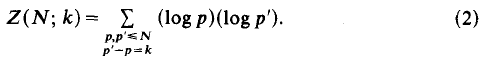Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Guy, Richard K.
1994.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
3.
Heath-Brown
2001.
Primes represented by x3+2y3.
Acta Mathematica,
Vol. 186,
Issue. 1,
p.
1.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
3.
Goldston, Daniel
Pintz, János
and
Yıldırım, Cem
2009.
Primes in tuples I.
Annals of Mathematics,
Vol. 170,
Issue. 2,
p.
819.
Kontorovich, Alex
2014.
Levels of Distribution and the Affine Sieve.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 23,
Issue. 5,
p.
933.
Coppola, Giovanni
and
Laporta, Maurizio
2018.
Correlations and distribution of essentially bounded functions in short intervals.
Afrika Matematika,
Vol. 29,
Issue. 7-8,
p.
1245.
Coppola, Giovanni
and
Laporta, Maurizio
2018.
Sieve Functions in Arithmetic Bands, II.
Indian Journal of Pure and Applied Mathematics,
Vol. 49,
Issue. 2,
p.
301.
Iovane, Gerardo
Di Gironimo, Patrizia
Benedetto, Elmo
and
D’Alfonso, Vittorio
2024.
Some Properties and Algorithms for Twin Primes.
Applied Sciences,
Vol. 14,
Issue. 17,
p.
7902.
Tsuda, Yusuke
2025.
Small gaps between primes that satisfy the Goldbach equation.
Monatshefte für Mathematik,
Vol. 206,
Issue. 1,
p.
217.