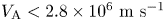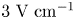1. Introduction
Open magnetic systems for plasma confinement regained interest in the last decade (Bagryansky, Beklemishev & Postupaev Reference Bagryansky, Beklemishev and Postupaev2019). Recent advances in plasma stability and suppression of the axial energy and particle losses (Burdakov et al. Reference Burdakov, Azhannikov, Astrelin, Beklemishev, Burmasov, Derevyankin, Ivanenko, Ivanov, Ivantsivskiy and Kandaurov2007; Bagryansky et al. Reference Bagryansky, Anikeev, Denisov, Gospodchikov, Ivanov, Lizunov, Kovalenko, Malygin, Maximov and Korobeinikova2015; Gota et al. Reference Gota, Binderbauer, Tajima, Putvinski, Tuszewski, Deng, Dettrick, Gupta, Korepanov and Magee2019) led to proposals of the next generation of mirror machines (Yakovlev et al. Reference Yakovlev, Chen, Bagryansky, Bragin, Kotelnikov, Kuzmin, Prikhodko, Shikhovtsev, Usov and Wang2022; Endrizzi et al. Reference Endrizzi, Anderson, Brown, Egedal, Geiger, Harvey, Ialovega, Kirch, Peterson and Petrov2023; Skovorodin et al. Reference Skovorodin, Chernoshtanov, Amirov, Astrelin, Bagryansky, Beklemishev, Burdakov, Gorbovsky, Kotelnikov and Magommedov2023).
Multiple-mirror confinement is one of the possible ways to reduce axial particle and energy losses from the open trap (Budker, Mirnov & Ryutov Reference Budker, Mirnov and Ryutov1971; Lichtenberg & Lieberman Reference Lichtenberg and Lieberman1976; Burdakov & Postupaev Reference Burdakov and Postupaev2018). This method is proposed as one of the key features of the GDMT project (Beklemishev et al. Reference Beklemishev, Anikeev, Astrelin, Bagryansky, Burdakov, Davydenko, Gavrilenko, Ivanov, Ivanov and Ivantsivsky2013; Skovorodin et al. Reference Skovorodin, Chernoshtanov, Amirov, Astrelin, Bagryansky, Beklemishev, Burdakov, Gorbovsky, Kotelnikov and Magommedov2023). In this project, two-component plasma is confined in the central cell. The first component is the population of the energetic ions produced by the neutral beam injection. These ions are confined adiabatically and do not reach the mirrors. The second component is the thermalised warm plasma which is needed for kinetic stability. This component determines axial losses of particles and energy from the confinement zone. Multiple-mirror systems are intended for the suppression of these gas dynamic losses of the warm plasma. The multiple-mirror system has periodical magnetic field, therefore an ion can be trapped between the consequent maxima of the Yushmanov potential. Ion scattering leads to particle exchange between the trapped and the passing population. This scattering forms an effective friction force between the populations and, therefore, between the flowing plasma and the magnetic field. The friction force increases axial pressure gradient and reduces particle losses. The most effective momentum transfer requires comparable scale of the magnetic corrugation period and the ion mean free path ($\nu ^{*} = \lambda /h \sim 1$![]() ) (Kotelnikov Reference Kotelnikov2007). This criterion obviously cannot be fulfilled by the binary collisions in the hot plasma. Therefore, any process of anomalous ion scattering improves plasma confinement in the multiple-mirror trap. In GOL-3 multiple-mirror device, improved energy confinement time was observed at classical mean free path exceeding the period of the corrugation by two orders of magnitude, $\nu ^{*}_{{\rm classical}}\sim 0.01$
) (Kotelnikov Reference Kotelnikov2007). This criterion obviously cannot be fulfilled by the binary collisions in the hot plasma. Therefore, any process of anomalous ion scattering improves plasma confinement in the multiple-mirror trap. In GOL-3 multiple-mirror device, improved energy confinement time was observed at classical mean free path exceeding the period of the corrugation by two orders of magnitude, $\nu ^{*}_{{\rm classical}}\sim 0.01$![]() (Burdakov et al. Reference Burdakov, Azhannikov, Astrelin, Beklemishev, Burmasov, Derevyankin, Ivanenko, Ivanov, Ivantsivskiy and Kandaurov2007). The authors of the mentioned research associate this phenomenon with the scattering of the ions on the turbulence generated in separate cells of the multiple-mirror trap. This phenomenon is referred to as the anomalous ion scattering in this paper. The best possible option is to achieve the anomalous ion scattering by the intrinsic processes in the plasma without any external drive.
(Burdakov et al. Reference Burdakov, Azhannikov, Astrelin, Beklemishev, Burmasov, Derevyankin, Ivanenko, Ivanov, Ivantsivskiy and Kandaurov2007). The authors of the mentioned research associate this phenomenon with the scattering of the ions on the turbulence generated in separate cells of the multiple-mirror trap. This phenomenon is referred to as the anomalous ion scattering in this paper. The best possible option is to achieve the anomalous ion scattering by the intrinsic processes in the plasma without any external drive.
Our research is focused on the specific type of multiple-mirror confinement with moving magnetic mirrors. Moving corrugation was proposed soon after the multiple-mirror itself (Budker, Mirnov & Ryutov Reference Budker, Mirnov and Ryutov1982) but has never been tested in experiment due to excessive power needed for fast switching of the high-field magnetic system. Helical mirror confinement is a modification of the moving-mirrors idea (Beklemishev Reference Beklemishev2013). Periodic variations of the magnetic field are arranged in the helically symmetric form. In the reference frame of the rotating plasma, the periodical variations of the magnetic field move in the direction defined by the directions of the rotation and the helicity. The locally trapped particles gain additional momentum in the same direction. Motion of the rotating plasma in a helical magnetic field was described theoretically by Beklemishev (Reference Beklemishev2016) and Chernoshtanov & Ayupov (Reference Chernoshtanov and Ayupov2021).
The idea of the helical confinement was experimentally tested in the small-scale helical mirror SMOLA in the Budker INP (Sudnikov et al. Reference Sudnikov, Beklemishev, Postupaev, Ivanov, Inzhevatkina, Sklyarov, Burdakov, Kuklin, Rovenskikh and Melnikov2019, Reference Sudnikov, Beklemishev, Inzhevatkina, Ivanov, Postupaev, Burdakov, Glinsky, Kuklin, Rovenskikh and Ustyuzhanin2020). Good agreement of the confinement effectiveness with the theory was found (Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Lomov, Postupaev, Tolkachev and Ustyuzhanin2022a). One of the most interesting effects was the effectiveness at low plasma densities, when the ion mean free path is an order of magnitude larger than the corrugation period (Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Postupaev, Sklyarov, Tolkachev and Ustyuzhanin2022b). The confinement is also associated with the electric potential fluctuations. In this paper, we present the parameters of fluctuations observed in the helically corrugated multiple-mirror trap and investigate their capability to induce anomalous ion scattering as in the GOL-3 experiment mentioned previously.
2. Theoretical consideration
The main difference between regular and moving multiple mirrors is non-zero axial velocity of the trapped particles. In the case of the helical corrugation this velocity is estimated as $v_z \approx \omega _{E\times B}h/2{\rm \pi}$![]() , where $\omega _{E\times B}$
, where $\omega _{E\times B}$![]() is the angular velocity and $h$
is the angular velocity and $h$![]() is the corrugation period. In the general case, this velocity can be chosen arbitrary. We assume later that the axial velocity of the trapped ions is of the order of the ion thermal velocity, $v_z \sim v_i$
is the corrugation period. In the general case, this velocity can be chosen arbitrary. We assume later that the axial velocity of the trapped ions is of the order of the ion thermal velocity, $v_z \sim v_i$![]() (if $v_z\ll v_i$
(if $v_z\ll v_i$![]() , the force pumping the plasma seems to be weak, in case $v_z\gg v_i$
, the force pumping the plasma seems to be weak, in case $v_z\gg v_i$![]() it is too difficult to populate trapped ions). In our experiments axial velocity is about twice as high as the thermal velocity. Such non-equilibrium distribution function can be the source of free energy for instabilities.
it is too difficult to populate trapped ions). In our experiments axial velocity is about twice as high as the thermal velocity. Such non-equilibrium distribution function can be the source of free energy for instabilities.
The possibility of anomalous scattering depends on the energy transfer to the transiting ions. Building up anomalous scattering due to the intrinsic processes in the plasma requires the following energy transfer. External fields raise the kinetic energy of the trapped ions. They transfer the energy to the electrostatic or electromagnetic waves. The turbulent energy cascade forms. Chaotic electric fields scatter the transiting ions. Turning off the energy transfer from the trapped particles to the wave and from the wave to the transiting particles results in impossibility to build up anomalous scattering by the energy of the non-equilibrium distribution function. Here we focus mostly on the energy transfer from the trapped ions to the wave.
Let us consider now properties of the ion trajectories in the helical mirror and properties of the unstable wave. When ion motion is collisionless, the trajectories can be divided into trapped (axial velocity is close to the velocity of the helical corrugation in the rotating frame, the ion moves near the minimum of the magnetic field) and transiting. The guiding centre of the trapped ion moves along the banana-like trajectory on the plane $r \cos (\theta -2{\rm \pi} z/h)$![]() , $r \sin (\theta -2{\rm \pi} z/h)$
, $r \sin (\theta -2{\rm \pi} z/h)$![]() , where $r$
, where $r$![]() , $\theta$
, $\theta$![]() and $z$
and $z$![]() are the cylindrical coordinates. Thus, the trajectory of the trapped ion coincides approximately with the helical line $r={\rm const.}$
are the cylindrical coordinates. Thus, the trajectory of the trapped ion coincides approximately with the helical line $r={\rm const.}$![]() , $\theta =2{\rm \pi} z/h+{\rm const}$
, $\theta =2{\rm \pi} z/h+{\rm const}$![]() . This line lies on the magnetic surface and coincides with the line of the minimal magnetic field magnitude.
. This line lies on the magnetic surface and coincides with the line of the minimal magnetic field magnitude.
The unstable wave can interact effectively with the trapped ions if the phase of the wave is constant along the trajectory of the trapped ion. If the helical corrugation is weak and the plasma is approximately cylindrical, the electric field of the wave can be approximately written in the form
The wave phase along the trapped ion trajectory is approximately $(k_{\|}v_z+2{\rm \pi} mv_z/h-\omega )t$![]() . The phase is constant when the wave frequency satisfies the condition
. The phase is constant when the wave frequency satisfies the condition
The wave frequency measured in the experiment is relatively low, $\omega \ll \omega _{E\times B}$![]() . There are two possibilities. First, the wave can be axisymmetric, $m=0$
. There are two possibilities. First, the wave can be axisymmetric, $m=0$![]() , and the wavelength is large (of the order of length of helical mirror $L$
, and the wavelength is large (of the order of length of helical mirror $L$![]() )
)
If the axial electric field component of the wave is not equal to zero and the wave period is of the order of the ion transit time $L/vt$![]() , the electric field changes slowly on most of the ion trajectories. Then the wave can decelerate outflow ions and increase its own amplitude.
, the electric field changes slowly on most of the ion trajectories. Then the wave can decelerate outflow ions and increase its own amplitude.
On the other hand, the condition $\omega \ll \omega _{E\times B}$![]() is possible if $m \neq 0$
is possible if $m \neq 0$![]() and the wavelength is several times less than the helical pitch,
and the wavelength is several times less than the helical pitch,
In this case, the wave frequency is approximately $\omega _{E\times B}$![]() and the axial phase velocity is $\omega _{E\times B}/k_{\|} \approx mv_z \sim mv_i$
and the axial phase velocity is $\omega _{E\times B}/k_{\|} \approx mv_z \sim mv_i$![]() in a frame of reference rotating with the frequency $\omega _{E\times B}$
in a frame of reference rotating with the frequency $\omega _{E\times B}$![]() . In the case $m=1$
. In the case $m=1$![]() the phase velocity is of the order of the thermal velocity of ions. Thus, the wave electric field is approximately constant along the ion trajectories and such a wave also can decelerate ions.
the phase velocity is of the order of the thermal velocity of ions. Thus, the wave electric field is approximately constant along the ion trajectories and such a wave also can decelerate ions.
In a chaotic electric field the transiting ion receives random additions to its transverse velocity
where $q$![]() and $m_{\rm i}$
and $m_{\rm i}$![]() are the ion charge and mass, $\delta E$
are the ion charge and mass, $\delta E$![]() is the characteristic value of the electric field and $\tau \sim \delta /v_{\rm Ti}$
is the characteristic value of the electric field and $\tau \sim \delta /v_{\rm Ti}$![]() is the time of the flight through the region of the invariable field. The ion experiences $N \sim h / \delta$
is the time of the flight through the region of the invariable field. The ion experiences $N \sim h / \delta$![]() small-angle scatterings during passing through the distance of a corrugation period. Then its pitch angle should be changed by $\Delta \theta \sim 1$
small-angle scatterings during passing through the distance of a corrugation period. Then its pitch angle should be changed by $\Delta \theta \sim 1$![]() :
:

It can be satisfied if the mean electric field is
Simple estimation of the length of the invariable field region can be based on the wavelength obtained in (2.4), $\delta \lesssim h/(2{\rm \pi} m)$![]() . Helix pitch length equals $18\ {\rm cm}$
. Helix pitch length equals $18\ {\rm cm}$![]() for the SMOLA device. Assuming $m = 1$
for the SMOLA device. Assuming $m = 1$![]() , we obtain the characteristic electric field $\delta E \gtrsim 1\ {\rm V}\ {\rm cm}^{-1}$
, we obtain the characteristic electric field $\delta E \gtrsim 1\ {\rm V}\ {\rm cm}^{-1}$![]() in the SMOLA case.
in the SMOLA case.
3. Experimental set-up and parameters
The layout of the SMOLA helical mirror is presented in figure 1. The device was built for studies of a low-temperature hydrogen plasma flow through a 2.5-m-long transport section with the helically symmetric magnetic field. Plasma was generated in a source with a magnetically insulated heated LaB$_6$![]() cathode (Ivanov et al. Reference Ivanov, Ustyuzhanin, Sudnikov and Inzhevatkina2021). Then the plasma was injected into a compact mirror trap in the entrance tank. Hereinafter this is referred to as the confinement region. In the discussed experiments, these trap mirrors were asymmetric with mirror ratios $R \approx 8$
cathode (Ivanov et al. Reference Ivanov, Ustyuzhanin, Sudnikov and Inzhevatkina2021). Then the plasma was injected into a compact mirror trap in the entrance tank. Hereinafter this is referred to as the confinement region. In the discussed experiments, these trap mirrors were asymmetric with mirror ratios $R \approx 8$![]() on the plasma source side and $R \approx 3$
on the plasma source side and $R \approx 3$![]() on the helical mirror side. Plasma flows in the axial direction from the confinement region to the transport section. This section has two independent magnetic systems, a solenoid for a straight field and a bispiral helical winding that forms helical magnetic mirrors. The spiral has $N = 12$
on the helical mirror side. Plasma flows in the axial direction from the confinement region to the transport section. This section has two independent magnetic systems, a solenoid for a straight field and a bispiral helical winding that forms helical magnetic mirrors. The spiral has $N = 12$![]() corrugation periods. We denote the fieldline without the periodic variation of the magnetic field module as the magnetic axis of the transport section. This axis has a spiral shape, its radius depends on the helical to axial components of the magnetic field ratio. The last part of the device is the exit expander that contains an exit limiter and radially segmented plasma receiver endplates. The axially symmetric confinement region, the helically symmetric transport section and the axially symmetric exit expander are matched together by the special correction units. The centre of the cathode is projected by the magnetic fieldline to the magnetic axis of the transport section and to the centre of the endplates. A detailed description of the device can be found in Sudnikov et al. (Reference Sudnikov, Beklemishev, Postupaev, Burdakov, Ivanov, Vasilyeva, Kuklin and Sidorov2017).
corrugation periods. We denote the fieldline without the periodic variation of the magnetic field module as the magnetic axis of the transport section. This axis has a spiral shape, its radius depends on the helical to axial components of the magnetic field ratio. The last part of the device is the exit expander that contains an exit limiter and radially segmented plasma receiver endplates. The axially symmetric confinement region, the helically symmetric transport section and the axially symmetric exit expander are matched together by the special correction units. The centre of the cathode is projected by the magnetic fieldline to the magnetic axis of the transport section and to the centre of the endplates. A detailed description of the device can be found in Sudnikov et al. (Reference Sudnikov, Beklemishev, Postupaev, Burdakov, Ivanov, Vasilyeva, Kuklin and Sidorov2017).

Figure 1. Layout of the SMOLA helical mirror. Position of the main diagnostics is indicated. Probe: Set of electrostatic probes including two or more emissive probes and a double or Mach probe. D.Sp: Doppler spectroscopy. $\dot B$![]() : 12-channel array of Mirnov coils. 38 GHz: microwave interferometer.
: 12-channel array of Mirnov coils. 38 GHz: microwave interferometer.
The distribution of the guiding magnetic field is shown in figure 2. Later in this paper, the magnetic configuration is referred to by the guiding magnetic field in the transport section; all other magnetic fields vary proportionally. Another parameter of the magnetic system is the mean corrugation ratio $R_{{\rm mean}}$![]() , which is the ratio of the maximal and the minimal magnetic field along the fieldline within the transport section averaged over the plasma cross-section. This parameter defines the fraction of locally trapped particles in the plasma. In the discussed experiments, the magnetic field was in the range $B_z = 50\unicode{x2013}100\ \text {mT}$
, which is the ratio of the maximal and the minimal magnetic field along the fieldline within the transport section averaged over the plasma cross-section. This parameter defines the fraction of locally trapped particles in the plasma. In the discussed experiments, the magnetic field was in the range $B_z = 50\unicode{x2013}100\ \text {mT}$![]() , and the mean corrugation ratio was $R_{{\rm mean}} = 1.52$
, and the mean corrugation ratio was $R_{{\rm mean}} = 1.52$![]() .
.

Figure 2. Guiding magnetic field profiles for different radii.
The experiments described in this paper were focused on the oscillations of the electrostatic potential in the transport section with the helical magnetic field and their possibility of meeting the criteria of the anomalous scattering. The main diagnostics for these oscillations were radially movable sets of the electrostatic probes in the different positions along the transport section ($z = 2.04$![]() m, 2.4 m, 2.58 m, 2.94 m and 3.48 m). The sets had the following arrangement of the emissive probes. The probe sets at the coordinates 2.58 m, 2.94 m and 3.48 m consist of two radially shifted electrodes. The set at $z = 2.04$
m, 2.4 m, 2.58 m, 2.94 m and 3.48 m). The sets had the following arrangement of the emissive probes. The probe sets at the coordinates 2.58 m, 2.94 m and 3.48 m consist of two radially shifted electrodes. The set at $z = 2.04$![]() m consist of two probe assemblies separated azimuthally by $180^{\circ }$
m consist of two probe assemblies separated azimuthally by $180^{\circ }$![]() and located at same $r$
and located at same $r$![]() for discussed experiments. In both assemblies the electrodes are shifted radially. The set at $z = 2.4$
for discussed experiments. In both assemblies the electrodes are shifted radially. The set at $z = 2.4$![]() m consists of seven individual electrodes: five of them are distributed along the vertical chord and two are shifted radially and axially relative to the central electrode of the vertical chord. The distances between the neighbouring electrodes in all assemblies are 1 cm. The thoriated tungsten electrodes were heated by the plasma during the initial part of the discharge and then provided simultaneous measurements of plasma potential and radial electric field. Reaching the working temperature of the probe was verified by the thermal radiation of the wire.
m consists of seven individual electrodes: five of them are distributed along the vertical chord and two are shifted radially and axially relative to the central electrode of the vertical chord. The distances between the neighbouring electrodes in all assemblies are 1 cm. The thoriated tungsten electrodes were heated by the plasma during the initial part of the discharge and then provided simultaneous measurements of plasma potential and radial electric field. Reaching the working temperature of the probe was verified by the thermal radiation of the wire.
Each of these sets included also a double or Mach probe. Double probes were used alternately in the ion saturation or in the $I$![]() –$V$
–$V$![]() characteristic regime. Plasma density in the confinement region was measured by the radially movable double probe at $z = 0.4$
characteristic regime. Plasma density in the confinement region was measured by the radially movable double probe at $z = 0.4$![]() m. Other parts of the diagnostic complex (imaging Doppler spectrometers, an array of Mirnov coils and a microwave interferometer) were also used to control the discharge parameters.
m. Other parts of the diagnostic complex (imaging Doppler spectrometers, an array of Mirnov coils and a microwave interferometer) were also used to control the discharge parameters.
The plasma density between the mirrors in the confinement region was determined by the hydrogen flow rate from the gas feeding system into the plasma source. The density was in the range $n = (0.5\unicode{x2013}5.5)\times 10^{18}\ \text {m}^{-3}$![]() for the confinement region, the average ion temperature was $T_{\rm i} = 3.5\unicode{x2013}4.5\ \text {eV}$
for the confinement region, the average ion temperature was $T_{\rm i} = 3.5\unicode{x2013}4.5\ \text {eV}$![]() and the electron temperature on the axis was $T_{\rm e} = 20\unicode{x2013}30\ \text {eV}$
and the electron temperature on the axis was $T_{\rm e} = 20\unicode{x2013}30\ \text {eV}$![]() (Ivanov et al. Reference Ivanov, Ustyuzhanin, Sudnikov and Inzhevatkina2021; Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Postupaev, Sklyarov, Tolkachev and Ustyuzhanin2022b). The density in the entrance region of the transport section was roughly half that in all regimes, giving $n = (0.2\unicode{x2013}2.5)\times 10^{18}\ \text {m}^{-3}$
(Ivanov et al. Reference Ivanov, Ustyuzhanin, Sudnikov and Inzhevatkina2021; Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Postupaev, Sklyarov, Tolkachev and Ustyuzhanin2022b). The density in the entrance region of the transport section was roughly half that in all regimes, giving $n = (0.2\unicode{x2013}2.5)\times 10^{18}\ \text {m}^{-3}$![]() . The typical plasma density profiles for $B = 70\ \text {mT}$
. The typical plasma density profiles for $B = 70\ \text {mT}$![]() at axial coordinates $z=0.4\ \text {m}$
at axial coordinates $z=0.4\ \text {m}$![]() and $z=2.04\ \text {m}$
and $z=2.04\ \text {m}$![]() are presented in figure 3(a,c). These values correspond to the mean free path of the ion in the helical field with respect to the binary collisions $\lambda = 0.3\unicode{x2013}2.5\ \text {m}$
are presented in figure 3(a,c). These values correspond to the mean free path of the ion in the helical field with respect to the binary collisions $\lambda = 0.3\unicode{x2013}2.5\ \text {m}$![]() . Therefore, the ratio of the mean free path to the period of the helical corrugation was $\lambda /h \sim 1$
. Therefore, the ratio of the mean free path to the period of the helical corrugation was $\lambda /h \sim 1$![]() on the high-density bound (in most high-density cases $\lambda \approx 2h$
on the high-density bound (in most high-density cases $\lambda \approx 2h$![]() ) and $\lambda /h \sim N$
) and $\lambda /h \sim N$![]() on the low-density bound. The first case meets the criterion of an efficient multiple-mirror confinement with binary collisions only, the second requires anomalous scattering for the flow suppression. The helical mirror concept requires fast rotation of plasma due to $E\times B$
on the low-density bound. The first case meets the criterion of an efficient multiple-mirror confinement with binary collisions only, the second requires anomalous scattering for the flow suppression. The helical mirror concept requires fast rotation of plasma due to $E\times B$![]() drift. Plasma rotation velocity in the discussed experiments was $\omega = (1\unicode{x2013}1.1)\times 10^6\ \text {s}^{-1}$
drift. Plasma rotation velocity in the discussed experiments was $\omega = (1\unicode{x2013}1.1)\times 10^6\ \text {s}^{-1}$![]() in the entrance tank ($z = 1.15$
in the entrance tank ($z = 1.15$![]() m). Radial electric field in the plasma (figure 3b,d) is consistent with the rotation velocity. Electric field increases roughly linearly in the inner part of the plasma column (inside the projection of the cathode of the plasma source) and decreases to zero on the plasma edge. According to the radial electric field measurements the plasma rotation velocity profiles in the transport section are identical within error bars.
m). Radial electric field in the plasma (figure 3b,d) is consistent with the rotation velocity. Electric field increases roughly linearly in the inner part of the plasma column (inside the projection of the cathode of the plasma source) and decreases to zero on the plasma edge. According to the radial electric field measurements the plasma rotation velocity profiles in the transport section are identical within error bars.

Figure 3. Experimental profiles of (a) the plasma density $n$![]() in coordinate $z=2.04\ \text {m}$
in coordinate $z=2.04\ \text {m}$![]() , (b) the electric field $E_r$
, (b) the electric field $E_r$![]() in coordinate $z=2.04\ \text {m}$
in coordinate $z=2.04\ \text {m}$![]() , (c) the plasma density $n$
, (c) the plasma density $n$![]() in coordinate $z=0.4\ \text {m}$
in coordinate $z=0.4\ \text {m}$![]() and (d) the electric field $E_r$
and (d) the electric field $E_r$![]() in coordinate $z=0.4\ \text {m}$
in coordinate $z=0.4\ \text {m}$![]() .
.
4. Signal analysis procedure
The fluctuation properties were obtained by the Fourier-based cross-correlation function analysis. This method is widely used for the investigation of plasma fluctuation in various magnetic field geometries (Turner, Powers & Simonen Reference Turner, Powers and Simonen1977; Kim et al. Reference Kim, Edgell, Greene, Strait and Chance1999; Melnikov et al. Reference Melnikov, Eliseev, Jiménez-Gómez, Ascasibar, Hidalgo, Chmyga, Komarov, Kozachok, Krasilnikov and Khrebtov2010). It extracts the most significant spectrum components and its phase difference between spatially separated channels. According to the convolution theorem the cross-spectrum of two signals is equal to the pointwise product of the signals spectra:
Here $\mathfrak {F}[.]$![]() denotes the Fourier transform, $s_i$
denotes the Fourier transform, $s_i$![]() denotes processing signals and $\text {cov }(. , .)$
denotes processing signals and $\text {cov }(. , .)$![]() denotes the cross-covariation function. Thus, the frequencies with high amplitude in both spectra have a high one in cross-spectrum. The cross-coherence, $\gamma _{1,2}$
denotes the cross-covariation function. Thus, the frequencies with high amplitude in both spectra have a high one in cross-spectrum. The cross-coherence, $\gamma _{1,2}$![]() , can be used to determine the significance of the component:
, can be used to determine the significance of the component:
Here angle brackets denote averaging over multiple signals’ samples. The argument of the product corresponds to the phase shift between two same-frequency Fourier components of the signals:
Knowing the phase shifts between two Fourier components and the distance between the diagnostics registered them one can explore spatial structure of these components. It is natural for cylindrically shaped plasma to treat fluctuations in terms of azimuthal ($k_\theta$![]() ), radial ($k_r$
), radial ($k_r$![]() ) and axial ($k_z$
) and axial ($k_z$![]() ) wavenumbers. One has to use probes separated in the directions listed above to obtain these wavenumbers.
) wavenumbers. One has to use probes separated in the directions listed above to obtain these wavenumbers.
Plasma potential was measured by emissive probes. The probes formed the sets allowing $k_r$![]() , $k_\theta$
, $k_\theta$![]() and $k_z$
and $k_z$![]() to be obtained. The arrangement of the electrodes is described in § 3. Since the probes arranged along the vertical chord are separated both by radial and azimuthal coordinates, the phase difference between any pair has both $k_r$
to be obtained. The arrangement of the electrodes is described in § 3. Since the probes arranged along the vertical chord are separated both by radial and azimuthal coordinates, the phase difference between any pair has both $k_r$![]() and $k_\theta$
and $k_\theta$![]() contribution. Considering one of the probes as the point of reference we obtain a linear system of ordinary equations of the form $\Delta \phi _i = k_r\times r_i + m\times \Delta \theta _i$
contribution. Considering one of the probes as the point of reference we obtain a linear system of ordinary equations of the form $\Delta \phi _i = k_r\times r_i + m\times \Delta \theta _i$![]() . Here $m$
. Here $m$![]() is the mode number, $\Delta r_i$
is the mode number, $\Delta r_i$![]() and $\Delta \theta _i$
and $\Delta \theta _i$![]() are the radial and azimuthal distances, respectively, between $i$
are the radial and azimuthal distances, respectively, between $i$![]() th and base probes. This system is solvable by the least-squares method (LSM). This probe set was also rotated by $90^{\circ }$
th and base probes. This system is solvable by the least-squares method (LSM). This probe set was also rotated by $90^{\circ }$![]() for more precise measurement of $k_z$
for more precise measurement of $k_z$![]() . The radial coordinate of each set was varied to obtain radial profiles.
. The radial coordinate of each set was varied to obtain radial profiles.
5. Spatial and temporal spectra of the fluctuations
The typical experimental waveforms are shown in figure 4. Time $t=0$![]() corresponds to the discharge initiation. The stationary plasma discharge builds up during the first 40 ms. Stationary neutral gas distribution, which depends on the hydrogen flow rate in the plasma source, discharge current and configuration, is achieved in $\sim 80\ \text {ms}$
corresponds to the discharge initiation. The stationary plasma discharge builds up during the first 40 ms. Stationary neutral gas distribution, which depends on the hydrogen flow rate in the plasma source, discharge current and configuration, is achieved in $\sim 80\ \text {ms}$![]() . The emissive probe reaches working temperature in $t\leq 40\ \text {ms}$
. The emissive probe reaches working temperature in $t\leq 40\ \text {ms}$![]() at radial coordinates $r\leq 6\ \text {cm}$
at radial coordinates $r\leq 6\ \text {cm}$![]() . At the outer region ($r=6\unicode{x2013}8\ \text {cm}$
. At the outer region ($r=6\unicode{x2013}8\ \text {cm}$![]() ) the heating takes up to $t=90\ \text {ms}$
) the heating takes up to $t=90\ \text {ms}$![]() . The temperature rise time is consistent with the estimations similar to (Hershkowitz et al. Reference Hershkowitz, Nelson, Pew and Gates1983). At $t=165\ \text {ms}$
. The temperature rise time is consistent with the estimations similar to (Hershkowitz et al. Reference Hershkowitz, Nelson, Pew and Gates1983). At $t=165\ \text {ms}$![]() the plasma source switches off to avoid damaging the probes. The parts of signals corresponding to the stationary stage of the discharge were used for analysis. The ADC sample rate (50 MS s$^{-1}$
the plasma source switches off to avoid damaging the probes. The parts of signals corresponding to the stationary stage of the discharge were used for analysis. The ADC sample rate (50 MS s$^{-1}$![]() ) allows us to treat the fluctuation with frequency up to 25 MHz. The ADC output of the full length signal is decimated in order to save storage space. The resulting sample rate allows us to analyse frequencies up to 390 kHz. In addition, the short samples of the steady phase signals ($t=131.1\unicode{x2013}136.3\ \text {ms}$
) allows us to treat the fluctuation with frequency up to 25 MHz. The ADC output of the full length signal is decimated in order to save storage space. The resulting sample rate allows us to analyse frequencies up to 390 kHz. In addition, the short samples of the steady phase signals ($t=131.1\unicode{x2013}136.3\ \text {ms}$![]() ) are recorded with original sample rate allowing us to investigate high-frequency fluctuations.
) are recorded with original sample rate allowing us to investigate high-frequency fluctuations.

Figure 4. Typical waveforms of plasma parameters in discharges with $R_{{\rm mean}} = 1.52$![]() , $B_z = 70\ \text {mT}$
, $B_z = 70\ \text {mT}$![]() and plasma density $n = 5.1\times 10^{18}\ \text {m}^{-3}$
and plasma density $n = 5.1\times 10^{18}\ \text {m}^{-3}$![]() at $z = 0.4\ \text {m}$
at $z = 0.4\ \text {m}$![]() and $n = 2.1 \times 10^{18}\ \text {m}^{-3}$
and $n = 2.1 \times 10^{18}\ \text {m}^{-3}$![]() at $z = 2.04\ \text {m}$
at $z = 2.04\ \text {m}$![]() : (a) the discharge current; (b) the voltage between the anode and the cathode of the plasma source; (c) the radial electric field component at z = 2.04 m; (d) the potential of the emissive probes at z = 2.04 m and $r = 58$
: (a) the discharge current; (b) the voltage between the anode and the cathode of the plasma source; (c) the radial electric field component at z = 2.04 m; (d) the potential of the emissive probes at z = 2.04 m and $r = 58$![]() and $48\ \text {mm}$
and $48\ \text {mm}$![]() . Solid lines on the panels (a–d) show moving average, shaded areas correspond to the amplitude of the observed oscillations. Panels (e–h) show waveforms of the oscillations in the short time fragment.
. Solid lines on the panels (a–d) show moving average, shaded areas correspond to the amplitude of the observed oscillations. Panels (e–h) show waveforms of the oscillations in the short time fragment.
The oscillations of the potentials and the electric field are shown in figure 4(e–h). One can see the delay between the oscillations of the potential on the probes shifted radially. Their Fourier spectra possess peaks in the frequency range of tens of kilohertz. The high-frequency rest of the spectrum decreases as $f^{-5/3}$![]() (shown in figure 5).
(shown in figure 5).

Figure 5. Emission probe signal spectrum for discharge with $B=70\ \text {mT}$![]() , $R_{{\rm mean}} = 1.52$
, $R_{{\rm mean}} = 1.52$![]() and density $n = 5.1 \times 10^{18}\ \text {m}^{-3}$
and density $n = 5.1 \times 10^{18}\ \text {m}^{-3}$![]() at $z=0.4\ \text {m}$
at $z=0.4\ \text {m}$![]() and $n = 2.1 \times 10^{18}\ \text {m}^{-3}$
and $n = 2.1 \times 10^{18}\ \text {m}^{-3}$![]() at $z = 2.04\ \text {m}$
at $z = 2.04\ \text {m}$![]() . The probe is located at $z = 2.04\ \text {m}$
. The probe is located at $z = 2.04\ \text {m}$![]() and $r = 58\ \text {mm}$
and $r = 58\ \text {mm}$![]() .
.
The outcome of the Fourier-based analysis is the dependencies of cross-coherence and cross-phase on time.
As an example, the cross-coherence and the cross-phase of the pair of two emission probes are presented in figure 6. The probes are located at $z = 2.04\ \text {m}$![]() and at $r = 28\ \text {mm}$
and at $r = 28\ \text {mm}$![]() and azimuthaly separated by $180^{\circ }$
and azimuthaly separated by $180^{\circ }$![]() . On the cross-coherence plot, two distinct high-coherent lines are pronouncedly visible. Cross-phase corresponding to these lines are constant during this part of discharge. The histograms are built by cross-phase sampling involving the entire investigated time period. They illustrate the statistical features of the discussed lines such as the mean value and width. Despite the fact that the spectra presented in figures 5 and 6 have two clearly visible peaks, the number of peaks can vary depending on experimental parameters. We discuss the fluctuation corresponding to the frequency about 30 kHz in figures 5 and 6 because this fluctuation was observed in wider range of experimental parameters.
. On the cross-coherence plot, two distinct high-coherent lines are pronouncedly visible. Cross-phase corresponding to these lines are constant during this part of discharge. The histograms are built by cross-phase sampling involving the entire investigated time period. They illustrate the statistical features of the discussed lines such as the mean value and width. Despite the fact that the spectra presented in figures 5 and 6 have two clearly visible peaks, the number of peaks can vary depending on experimental parameters. We discuss the fluctuation corresponding to the frequency about 30 kHz in figures 5 and 6 because this fluctuation was observed in wider range of experimental parameters.

Figure 6. (a) Coherence spectrogram, (b) cross-phase spectrogram and (c) cross-phase histogram of the emission probes separated by $180^{\circ }$![]() . The plasma density $n = 5.1 \times 10^{18}\ \text {m}^{-3}$
. The plasma density $n = 5.1 \times 10^{18}\ \text {m}^{-3}$![]() at $z = 0.4\ \text {m}$
at $z = 0.4\ \text {m}$![]() and $n = 2.1 \times 10^{18}\ \text {m}^{-3}$
and $n = 2.1 \times 10^{18}\ \text {m}^{-3}$![]() at $z = 2.04\ \text {m}$
at $z = 2.04\ \text {m}$![]() , $B = 70\ \text {mT}$
, $B = 70\ \text {mT}$![]() and $R_{{\rm mean}} = 1.52$
and $R_{{\rm mean}} = 1.52$![]() .
.
In the experiments discussed here, the frequency depends on the guiding magnetic field and the plasma density. To find out the form of this dependency, the fluctuation frequency was measured in the guiding magnetic field range $B_z=70\unicode{x2013}100\ \text {mT}$![]() at the plasma density $n = 2.17 \times 10^{17}\ \text {m}^{-3}-1.83 \times 10^{18}\ \text {m}^{-3}$
at the plasma density $n = 2.17 \times 10^{17}\ \text {m}^{-3}-1.83 \times 10^{18}\ \text {m}^{-3}$![]() at coordinate $z = 2.04\ \text {m}$
at coordinate $z = 2.04\ \text {m}$![]() . The resulting dependency of the frequency on the Alfvén velocity is presented in figure 7. This dependency is approximated by a linear function with the slope $1.7 \times 10^{-4}\ \text {cm}^{-1}$
. The resulting dependency of the frequency on the Alfvén velocity is presented in figure 7. This dependency is approximated by a linear function with the slope $1.7 \times 10^{-4}\ \text {cm}^{-1}$![]() for $V_{\rm A} < 2.8 \times 10^6\ \text {m}\ \text {s}^{-1}$
for $V_{\rm A} < 2.8 \times 10^6\ \text {m}\ \text {s}^{-1}$![]() . The function fits experimental data points with $R^2 = 0.9$
. The function fits experimental data points with $R^2 = 0.9$![]() . The Alfvén waves in cold plasma possess the same dependency on $V_{\rm A}$
. The Alfvén waves in cold plasma possess the same dependency on $V_{\rm A}$![]() in the low-frequency limit. For $V_{\rm A} > 2.8 \times 10^6\ \text {m}\ \text {s}^{-1}$
in the low-frequency limit. For $V_{\rm A} > 2.8 \times 10^6\ \text {m}\ \text {s}^{-1}$![]() the dependency is no longer considered as linear and goes to the plateau with frequency value 48 kHz.
the dependency is no longer considered as linear and goes to the plateau with frequency value 48 kHz.

Figure 7. Dependence of frequency on the Alfvén velocity. Different colours correspond to the different magnetic field values.
Calculating the cross-phase and varying the probe set's radial coordinate we have obtained the radial profile of the wavevector components (shown in figure 8). It is noteworthy that the plasma cross-section can be divided by radius into two zones. For $r$![]() values less than 40 mm, the radial and azimuthal wavenumbers undergo slight changes, remaining close to zero and between one and two, respectively. For larger radii, the wavenumbers’ absolute value increases but the signs are opposite. Meanwhile, the axial wavenumber has a global maximum at $r = 40$
values less than 40 mm, the radial and azimuthal wavenumbers undergo slight changes, remaining close to zero and between one and two, respectively. For larger radii, the wavenumbers’ absolute value increases but the signs are opposite. Meanwhile, the axial wavenumber has a global maximum at $r = 40$![]() mm. This radius is close to the position of the highest radial electric field. Inside this region, the electric field rises linearly. It corresponds to the rigid rotor rotation (angular velocity does not depend on the radius). The rotation of the plasma boundary has lower angular velocity.
mm. This radius is close to the position of the highest radial electric field. Inside this region, the electric field rises linearly. It corresponds to the rigid rotor rotation (angular velocity does not depend on the radius). The rotation of the plasma boundary has lower angular velocity.

Figure 8. (a) Radial component of the wavenumber, (b) mode number, (c) axial component of the wavenumber and (d) product of the wavevector axial component on the mode number of the wave for $B = 70\ \text {mT}, R_{{\rm mean}} = 1.52$![]() and $n = 5.1 \times 10^{18}\ \text {m}^{-3}$
and $n = 5.1 \times 10^{18}\ \text {m}^{-3}$![]() at $z = 0.4\ \text {m}$
at $z = 0.4\ \text {m}$![]() and $n = 2.1 \times 10^{18}\ \text {m}^{-3}$
and $n = 2.1 \times 10^{18}\ \text {m}^{-3}$![]() at $z = 2.04\ \text {m}$
at $z = 2.04\ \text {m}$![]() .
.
According to $k_r(r)$![]() (shown in figure 8), the fluctuation is in phase for $r < 45$
(shown in figure 8), the fluctuation is in phase for $r < 45$![]() mm. The radial size of this area can vary depending on the plasma parameters. In the periphery, sufficient $k_r$
mm. The radial size of this area can vary depending on the plasma parameters. In the periphery, sufficient $k_r$![]() appears and the fluctuation phase velocity is directed towards the magnetic axis.
appears and the fluctuation phase velocity is directed towards the magnetic axis.
The azimuthal mode number lies between 1 and 2 for $r < 40$![]() mm. For larger radii, the mode number increases. Mode number is positive and then the fluctuation azimuthal phase velocity is aligned with the ion rotation. The axial wavenumber has a maximum at $r = 40$
mm. For larger radii, the mode number increases. Mode number is positive and then the fluctuation azimuthal phase velocity is aligned with the ion rotation. The axial wavenumber has a maximum at $r = 40$![]() mm.
mm.
6. Discussion
According to the theory, the non-axisymmetric wave is in-phase with the trapped ions if the product of the azimuthal mode number and the axial wavelength, $m \times \lambda _z$![]() , is close to the helix pitch length (see (2.4)). This value is calculated from the $k_z$
, is close to the helix pitch length (see (2.4)). This value is calculated from the $k_z$![]() and $m$
and $m$![]() profiles in figure 8(b,c), and presented in figure 8(d). The wave structure satisfies the criterion discussed previously for $r$
profiles in figure 8(b,c), and presented in figure 8(d). The wave structure satisfies the criterion discussed previously for $r$![]() between 30 and 40 mm.
between 30 and 40 mm.
The electric field required for passing ions to be scattered is estimated from below in (2.7) and equals $1\ {\rm V}\ {\rm cm}^{-1}$![]() for the discussed experimental parameters. The experimental measurements of the observed wave amplitude is presented in figure 9. The observed amplitude is higher than estimated that suggests the wave to be powerful enough for causing the effective scattering, especially at the low-density limit. Amplitudes of all components of the electric field fluctuations decrease at the high-density limit and become close to the estimation mentioned previously. At the same time, the high-density limit does not require anomalous scattering for multiple-mirror confinement. At lower densities, the effective value of the electric field in the non-correlated continuous spectrum is high enough. Our a priori estimate (2.7) suggests $\delta \lesssim h/(2{\rm \pi} m)$
for the discussed experimental parameters. The experimental measurements of the observed wave amplitude is presented in figure 9. The observed amplitude is higher than estimated that suggests the wave to be powerful enough for causing the effective scattering, especially at the low-density limit. Amplitudes of all components of the electric field fluctuations decrease at the high-density limit and become close to the estimation mentioned previously. At the same time, the high-density limit does not require anomalous scattering for multiple-mirror confinement. At lower densities, the effective value of the electric field in the non-correlated continuous spectrum is high enough. Our a priori estimate (2.7) suggests $\delta \lesssim h/(2{\rm \pi} m)$![]() , which, in turn, relies on fulfillment of the condition (2.4). Then satisfying the condition (2.4) leads to achieving the amplitude required by (2.7) which is what we see in the experiment.
, which, in turn, relies on fulfillment of the condition (2.4). Then satisfying the condition (2.4) leads to achieving the amplitude required by (2.7) which is what we see in the experiment.

Figure 9. Experimental measurements of the observed wave amplitude: $E_{\rm rms}$![]() of the wave for $r=20\ \text {mm}$
of the wave for $r=20\ \text {mm}$![]() , $B_z = 70\ \text {mT}$
, $B_z = 70\ \text {mT}$![]() and $R_{{\rm mean}}=1.52$
and $R_{{\rm mean}}=1.52$![]() .
.
These observations show that the mechanism of the anomalous scattering described in § 2 is not prohibited by the wave structure or its amplitude. This mechanism may play a role in the previously observed improved confinement at lower densities (Sudnikov et al. Reference Sudnikov, Ivanov, Inzhevatkina, Larichkin, Postupaev, Sklyarov, Tolkachev and Ustyuzhanin2022b).
Despite the experimental observations that agrees with the theoretical assumptions, the following alternative hypotheses can be verified in future campaigns. Numerical calculations show that the scattering depends on the spatial spectrum of the chaotic wave. White noise with zero electric field along magnetic fieldlines does not show an effective scattering in the numerical models. Such kind of the chaotic spectrum was implied in the calculation as the simulation of the noise generated by the plasma source. In terms of (2.7), this field has much shorter length $\delta$![]() thus giving much higher required electric field fluctuation. Further numerical simulations will be directed on the more realistic description of the wave spectrum. At the same time, this model of the spectrum shows that the scattering of the passing ions may be caused by the correlated wave itself if the phase velocity of the wave is of the order of the ion thermal velocity and additional weak scattering due to rare Coulomb collisions (with free path compared with the length of the helical mirror) are present. The results of the simulation also emphasise the importance of the further experimental investigation of the chaotic spectrum properties and anomalous scattering at extremely low classical collisionality with $\nu ^{*}_{{\rm classical}} < 1/N$
thus giving much higher required electric field fluctuation. Further numerical simulations will be directed on the more realistic description of the wave spectrum. At the same time, this model of the spectrum shows that the scattering of the passing ions may be caused by the correlated wave itself if the phase velocity of the wave is of the order of the ion thermal velocity and additional weak scattering due to rare Coulomb collisions (with free path compared with the length of the helical mirror) are present. The results of the simulation also emphasise the importance of the further experimental investigation of the chaotic spectrum properties and anomalous scattering at extremely low classical collisionality with $\nu ^{*}_{{\rm classical}} < 1/N$![]() .
.
Another option to scatter the escaping ions is to increase their transverse energy by the Doppler-shifted radiofrequency wave (Miller et al. Reference Miller, Be'ery, Gudinetsky and Barth2023). This idea suggests that the wave in the frame of reference of the escaping ion should be in resonance with its gyromotion. Low frequency and low $k_z$![]() of the observed wave does not allow to achieve resonance condition in the central part of the plasma column. The significance of this mechanism on the periphery of the plasma column can be verified in further experiments with more detailed investigation of the spatial spectrum on the guiding magnetic field.
of the observed wave does not allow to achieve resonance condition in the central part of the plasma column. The significance of this mechanism on the periphery of the plasma column can be verified in further experiments with more detailed investigation of the spatial spectrum on the guiding magnetic field.
Further experiments can also address the verification of the possibility of achieving the required electric field, which depends linearly on the ion temperature, in hotter plasma. It requires additional ion heating in the experiment.
The dependence of the wave frequency on the Alfvén velocity suggests that the wave is of the Alfvén type for densities with $V_{\rm A} < 2.8\times 10^6\ \text {m}\ \text {s}^{-1}$![]() . The further investigation of the wave parameters such as polarisation and dispersion law for lower densities is necessary to verify this suggestion. The occurrence of the frequency plateau with $f = 48\ \text {kHz}$
. The further investigation of the wave parameters such as polarisation and dispersion law for lower densities is necessary to verify this suggestion. The occurrence of the frequency plateau with $f = 48\ \text {kHz}$![]() for $V_{\rm A} > 2.8\times 10^6\ \text {m}\ \text {s}^{-1}$
for $V_{\rm A} > 2.8\times 10^6\ \text {m}\ \text {s}^{-1}$![]() requires further study.
requires further study.
Acknowledgements
The authors thank Professor A. Burdakov, Dr D. Skovorodin, Dr A. Beklemishev and Professor I. Kotelnikov for valuable discussions.
Special Collection: Open Magnetic Systems for Plasma Confinement.
Editor C. Forest thanks the referees for their advice in evaluating this article.
Funding
This work was supported by a grant from the Russian Science Foundation 22-12-00133 (https://rscf.ru/project/22-12-00133/). Maintenance of the SMOLA device was supported by the Ministry of Science and Higher Education of the Russian Federation.
Declaration of interests
The authors report no conflict of interest.