Fragmentation of a fluid body into droplets underlies many contamination and disease transmission processes where pathogens are transported in a liquid phase. An important class of such processes involves formation of a fluid ligament and its destabilization into droplets. Inertial detachment (Gilet & Bourouiba, J. R. Soc. Interface, vol. 12, 2015, 20141092) is one of these modes: upon impact on a sufficiently compliant substrate, the substrate's motion can transfer its impulse to a contaminated sessile drop residing on it. The fragmentation of the sessile drop is efficient at producing contaminated ejected droplets with little dilution. Inertial detachment, particularly from substrates of intermediate wetting, is also interesting as a fundamental fragmentation process on its own merit, involving the asymmetric stretching of the sessile drop under impulsive axial forcing with one-sided pinning due to the substrate's intermediate wetting. Our experiments show that the radius, 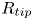 $R_{tip}$, of the tip drop ejected become insensitive to the Bond number value for
$R_{tip}$, of the tip drop ejected become insensitive to the Bond number value for 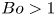 $Bo>1$. Here,
$Bo>1$. Here,  $Bo$ quantifies the inertial effects via the relative axial impulsive acceleration compared with capillarity. The time,
$Bo$ quantifies the inertial effects via the relative axial impulsive acceleration compared with capillarity. The time,  $t_{tip}$, of tip-drop breakup is also insensitive to
$t_{tip}$, of tip-drop breakup is also insensitive to  $Bo$. Combining experiments, theory and validated numerics, we decipher the selection of
$Bo$. Combining experiments, theory and validated numerics, we decipher the selection of 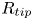 $R_{tip}$ and its sensitivity to the surface-wetting and substrate foot dynamics. Using asymptotic theory in the large
$R_{tip}$ and its sensitivity to the surface-wetting and substrate foot dynamics. Using asymptotic theory in the large 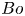 $Bo$ limit for which the thin-film/slender-jet approximations hold, we derive a reduced physical model that predicts
$Bo$ limit for which the thin-film/slender-jet approximations hold, we derive a reduced physical model that predicts  $R_{tip}$ consistent with our experiments. Finally, we discuss how pathogen physical properties (e.g. wetting and buoyancy) within the sessile drop determine their distribution in the tip and secondary fragmentation droplets.
$R_{tip}$ consistent with our experiments. Finally, we discuss how pathogen physical properties (e.g. wetting and buoyancy) within the sessile drop determine their distribution in the tip and secondary fragmentation droplets.