We study a weighted maximal weak-type inequality for Haar multipliers that can be regarded as a dual problem of Muckenhoupt and Wheeden. More precisely, if Tε is the Haar multiplier associated with the sequence ε with values in [−1, 1], and 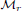 is the r-maximal operator, then for any weight w and any function f on [0, 1) we have
is the r-maximal operator, then for any weight w and any function f on [0, 1) we have
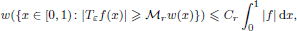
for some constant Cr depending only on r. We also show that the analogous result does not hold if we replace 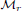 by the dyadic maximal operator Md. The proof rests on the Bellman function method; using this technique we establish related weighted Lp estimates for p close to 1, and then deduce the main result by extrapolation arguments.
by the dyadic maximal operator Md. The proof rests on the Bellman function method; using this technique we establish related weighted Lp estimates for p close to 1, and then deduce the main result by extrapolation arguments.

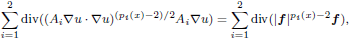
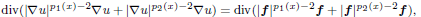
 =
=  is the
is the