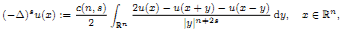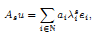In this paper we deal with two non-local operators that are both well known and widely studied in the literature in connection with elliptic problems of fractional type. More precisely, for a fixed s ∈ (0,1) we consider the integral definition of the fractional Laplacian given by

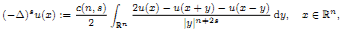
where c(n, s) is a positive normalizing constant, and another fractional operator obtained via a spectral definition, that is,

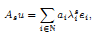
where ei, λi are the eigenfunctions and the eigenvalues of the Laplace operator −Δ in Ω with homogeneous Dirichlet boundary data, while ai represents the projection of u on the direction ei.

The aim of this paper is to compare these two operators, with particular reference to their spectrum, in order to emphasize their differences.

In this paper, we study the existence of infinitely many periodic solutions for the non-autonomous second-order Hamiltonian systems with symmetry. Based on the minimax methods in critical point theory, in particular, the fountain theorem of Bartsch and the symmetric mountain pass lemma due to Kajikiya, we obtain the existence results for both the superquadratic case and the subquadratic case, which unify and sharply improve some recent results in the literature.

We study the Helmholtz equation

in ℝd with magnetic and electric potentials that are singular at the origin and decay at ∞. We prove the existence of a unique solution satisfying a suitable Sommerfeld radiation condition, together with some a priori estimates. We use the limiting absorption method and a multiplier technique of Morawetz type.