The importance of matric algebras in Function Theory and in Physics (Birtwistle—The new Quantum Mechanics; and Courant and Hilbert—Methoden der mathematischen Physik) has resulted in comprehensive works on finite matrices. Very little progress has, however, been made in the necessary algebras of infinite matrices.

The sequence of orthogonal functions derived from Laguerre-polynomials is known to be complete, and hence closed, in L2 (0, ∞) if 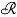(a) > − 1. In a recent paper Dr Kober introduced a generalisation of this sequence, which enables him to extend the known results also for 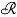(a) < − 1. Kober's guiding principle seems to be the following one: The Laguerre orthogonal functions form, for 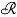(a) > − 1, a complete system of self and skew reciprocal functions of the Hankel transformation of order a. Now, if 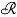(a) < − 1, the ordinary Hankel transform has to be replaced by so-called cut Hankel transform. Hence the system of functions which has to replace-Laguerre orthogonal functions when 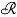(a) < − 1, should be a complete system of self and skew reciprocal functions of the cut Hankel transformation of order a, such that it reduces for 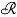(a) > − 1 (when the cut Hankel transform reduces to the ordinary one) to the sequence of Laguerre orthogonal functions. This, of course, is by no means a unique definition; nevertheless, together with what one would call the permanence of the Mellin transform, it enabled Kober to find a sequence of functions 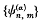which (i) reduces to the sequence of Laguerre orthogonal functions when 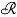(a) > − 1, m = 0, (ii) is a complete set of self and skew reciprocal functions of the cut Hankel transformation with kernel Ja, m and (iii) has the required qualities of completeness and closedness.

Let the set b1b2, b3, …., bk; of k non-negative integers be denoted by Bk. Let ξ;Bk denote the set ξb1 ξb2, ξb3, …. ξbk; ξ being any integer > 1. Without loss of generality, we can suppose that b ≦bi+1.

The theorems given here deal with the efficiency, mutual consistency, and regularity of γ-transformations.

§1. Theorem 1. The necessary and sufficient conditions that γ-matrices are efficient for all divergent series whose partial sums are bounded, are

where Δgk(a)≡gk(a)−gk+1(a).

The study of the primitive solutions of the equation

where A = (aij) is an n × n matrix whose elements are rational integers, was begun a long time ago. In most cases this equation occurred incidentally in another theory; for instance Jordan encountered it in connection with linear differential equations having algebraic solutions, Minkowski in connection with quadratic forms and Turnbull in geometry. An important fact about these matrices is that any unimodular matrix can be represented as the product of matrices with finite period.

The process of duplication of a linear algebra was defined in an earlier paper, where its occurrence in the symbolism of genetics was pointed out. The definition will now be repeated with an amplification. Although for purpose of illustration it is applied to the algebra of complex numbers, duplication will seem of no special significance if attention is fixed on algebras with associative multiplication and unique division; for duplication generally destroys these properties. The results to be proved, however, show that it is significant in connection with various other conceptions which appeared in the discussion of genetic algebras; namely baric algebras and train algebras (defined in G.A.), also nilpotent algebras, linear transformation and direct multiplication of algebras.

I have begun to study the laws of the struggle for life by a group of species living in the same environment in such a way that some devour others. I have used for this purpose the so called principle of encounter, considering the encounters of the individuals of the various species, and what follows by reason of the actions that the individuals exercise on one another.

§ 1. The object of this note is to discuss the formula

the integral being supposed convergent for certain ranges of values of x and z. The contour is such that the poles of Γ(– s)lie to its right and the other poles of the integrand to its left. It will be seen that all the Pincherle-Mellin-Barnes integrals are particular cases of this formula.

We suppose throughout that f(t) is periodic with period 2π, and Lebesgue-integrable in (− π, π).

We write

and suppose that the Fourier series of φ(t) and ψ(t) are respectively cos nt and sin nt. Then the Fourier series and allied series of f(t) at the point t = x are respectively and , where A0 = ½a0, An = ancos nx + bnsin nx, Bn = bncos nx − ansin nx and an, bn are the Fourier coefficients of f(t).

1. Points, n in number, A, B, C, D, E, … ., are taken at random in a plane, and through each is drawn a line in a random direction. The only condition imposed is that no two of these lines may be parallel.

(i). Two points A, B, define a circle S (AB) which passes through A, B and the intersection of the random lines through A and B. Its centre is denoted by (AB). Each pair of the points gives such a circle and centre.

Concerning your paper written in collaboration with Professor Copson, I found the expansion of

for small values of λ in the following manner: The elementary substitution tan ½φ = sin θ/(et + cos θ)yields

i.e. your equation (5.11).

Let , (n = 0, 1, ….) be the Laguerre, Hn(x) the Hermite polynomial. Let , be the space of all functions f(x) the pth powers of which are integrable over (a, b), with the norm

It is proposed to establish, by elementary methods, a theorem for matrices analogous to Fermat's Theorem in the Theory of Numbers. In Jordan's Traité des Substitutions (Paris, 1870) pp. 127, 128, the order of any given linear substitution or matrix A with reference to any prime number p is determined, but the result given depends on the particular characteristic equation satisfied by the matrix A, and a general result applicable to all matrices of n rows and n columns does not seem to have been published hitherto.

It has been pointed out that, in the paper by H. W. Richmond (Proceedings of the Edinburgh Mathematical Society (2), 6 (1940), 190-191), lines 3 and 4 of page 191 should read as follows:—Now the pencil includes two ruled cubic surfaces, one of them having 8′ as its double line and 7′ for the second line which the generators meet.

In a general metric space of four dimensions, with an interval given by , where – ds2 = gμνdxμdxν, where g = ║gμν║<0, we can choose locally galilean coordinates at any point. The initial directions of the axes can be fixed in an absolute fashion as the directions of the principal axes of the quadric Gμνdxμdxν = const., is the contracted Riemann-Christoffel tensor.

In a recent paper (these Proceedings (2), 6 (1939), 75–8), C. G. Lambe established, and gave some applications of, the formula

in which Ds is the symbol for the derivative of fractional order s. Lambe's proof of (1) is not quite rigorous and it does not bring out the conditions which have to be imposed upon f(x) in order to make (1) true. Furthermore this proof does not give any evidence as to the definition of fractional derivative which is to be used in connection with (1).

This note contains an elementary proof of the well-known result that every solution of Besse's equation

with a real parameter n has an infinite number of real positive zeros.

1. The object of this note is to discover a new function which is its own reciprocal in the Hankel Transform of order zero.

I will make use of the following theorem of Hardy and Titchmarsh1:–

A necessary and sufficient condition that a Junction f (x) should be its own Jv transform is that it should be of the form

where 0 < c < 1, and

It is well known that a non-ruled (i.e. not consisting of an infinity of lines) surface of order n lies in a space of not more than n dimensions n ≠ 4) and that for n > 9, the maximum dimension actually attained (here denoted by R) is certainly less than n.