Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T01:02:54.289Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Fourier coefficients of a discontinuous function

Published online by Cambridge University Press:  20 January 2009

S. P. Bhatnagar
S. P. Bhatnagar
Affiliation:
University College, London.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We suppose throughout that f(t) is periodic with period 2π, and Lebesgue-integrable in (− π, π).

We write

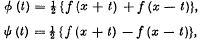
and suppose that the Fourier series of φ(t) and ψ(t) are respectively 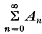cos nt and 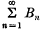sin nt. Then the Fourier series and allied series of f(t) at the point t = x are respectively 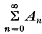and 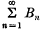, where A0 = ½a0, An = ancos nx + bnsin nx, Bn = bncos nx − ansin nx and an, bn are the Fourier coefficients of f(t).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 6 , Issue 4 , October 1941 , pp. 231 - 256
Copyright
Copyright © Edinburgh Mathematical Society 1941

References

REFERENCES

1.Bhatnagar, S. P., “A local property of the allied series of a Fourier series,”Proc. London Math. Soc. (2), 44 (1938), 315–322.CrossRefGoogle Scholar
2.Bosanquet, L. S., “On the summability of Fourier series,” Proc. London Math. Soc. (2), 31 (1930), 144–164.Google Scholar
3.Bosanquet, L. S., “Note on the limit of a function at a point,” Journal London Math. Soc, 7 (1932), 100–105.CrossRefGoogle Scholar
4.Bosanquet, L. S., “On the Cesàro summation of Fourier series and allied series,” Proc. London Math. Soc. (2), 37 (1934), 17–32.CrossRefGoogle Scholar
5.Bosanquet, L. S., “Some extensions of Young's criterion for the convergence of a Fourier series,” Quart. J. of Math. (Oxford series), 6 (1935), 113–123.Google Scholar
6.Bosanquet, L. S., “The absolute Cesàro surnmaljility of Fourier series,” Proc. London Math. Soc. (2), 41 (1936), 517–528.CrossRefGoogle Scholar
7.Bosanquet, L. S., ” Trans. Americm Math. Soc, 39 (1930), 189–204.Google Scholar
8.Bosanquet, L. S. and Offord, A. C., “A local property of Fourier series,” Proc. London Math. Soc. (2), 40 (1936), 273–280.CrossRefGoogle Scholar
9.Bosanquet, L. S. and Hyslop, J. M., “On the absolute summability of the allied series of a Fourier series,” Math. Zeitschrift, 42 (1937), 489–512.CrossRefGoogle Scholar
10.Csillag, P., “Korlátos ngadozàsu függvénysorok Fourier-fele állandóiról,” Math, ex Phys. Lapok, 27 (1918), 301–308.Google Scholar
11.Dienes, P., The Taylor series (Oxford, 1931).Google Scholar
12.Fejer, L., “Über die Bestimmung des Sprunges der Funktion aus ihrer Fourierreihe,” Journal fiir Math., 142 (1913),165–188.Google Scholar
13.Gergen, J. J., “Convergence and summability criteria for Fourier series,” Quart. J. of Math. (Oxford series), 1 (1930), 252–275.Google Scholar
14.Hardy, G. H. and Littlewood, J. E., “Solution of the Cesàro summability problem for power series and Fourier series,” Math. Zeitschrift, 19 (1924), 67–96.Google Scholar
14(a).Hardy, G. H., The allied series of a Fourier series. Proc. London Math. Soc. (2), 24 (1925), 211–246.Google Scholar
15.Hardy, G. H., “Notes on the theory of series (XVI): Two Tauberian theorems,” Journal London Math. Soc, 6 (1931),281–286.Google Scholar
16.Hobson, E. W., The theory of functions of a real variablt, 2 (Cambridge, 1926).Google Scholar
17.Hyslop, J. M., “On the approach of a series to its Cesàro limit,” Proc. Edinburgh Math. Soc. (2), 5 (1938), 182–201.Google Scholar
18.Jacob, M., “Beitrag zur Darstellung der Ableitungen eiuer Funktion durch ihre Fourier'sche Reihe,” Bull, de l'Académie Polonaise (Cracovie) (A) (1927), 287–294.Google Scholar
19.Kogbetliantz, E., “Sur les séries absolument sommables par la mèthode des moyennes arithmétiques,” Butt, des Sci. Math. (2), 49 (1925), 234–256.Google Scholar
20.Kogbetliantz, E., “Sommation des series et integrates divergentes par les moyennes arithmetiques et typiques,” Memorial des Sciences Math., 51 (1931), 1–84.Google Scholar
21.Obrechkoff, N., “Sur la sommation des séries trigonométriques de Fourier par les moyennes arithmétiques,” Bull, de la Soc. Math, de France, 62 (1934), 84–109 and 167–184.Google Scholar
22.Paley, R. E. A. C., “On the Cesáro summability of Fourier series and allied series,” Proc. Cambridge Phil. Soc, 26 (1930), 173–203.Google Scholar
23.Szidon, S., “A függveny ugrásának meghatározása a fugvény Fourier-féle sorábóle,” Math, is Termés. Ért., 27 (1918), 309–311.Google Scholar
24.Szász, O., “über die Arithmetischen Mittel Fourierscher Reihen,” Acta Math., 48 (1936), 353–362.CrossRefGoogle Scholar
25.Titchmarsh, E. C., “The order of magnitude of the coefficients in a generalised Fourier series,” Proc. London Math. Soc. (2), 22 (1923), xxv–xxvi.Google Scholar
26.Young, W. H., “On the order of magnitude of the coefficients of a Fourier series,” Proc. Royal Soc. (A), 93 (1916), 42–55.Google Scholar
27.Zygmund, A., “Sur un théoréme de M. Gronwall,” Bull, de l' Acad. Polonaise (Gracovie) (A) (1925), 207–217.Google Scholar