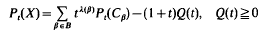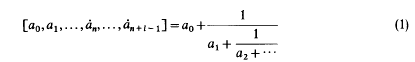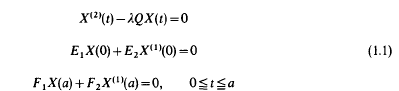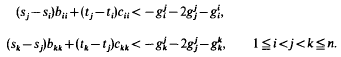Research Article
The natural partial order on an abundant semigroup
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 169-186
-
- Article
-
- You have access
- Export citation
Divisible S-systems and R-modules
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 187-200
-
- Article
-
- You have access
- Export citation
On the automorphisms of the group ring of a unique product group
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 201-205
-
- Article
-
- You have access
- Export citation
On the centre and residual finiteness of the automorphism group of a group ring
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 207-213
-
- Article
-
- You have access
- Export citation
Elliptic multiparameter eigenvalue problems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 215-228
-
- Article
-
- You have access
- Export citation
The space of totally bounded analytic functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 229-246
-
- Article
-
- You have access
- Export citation
Geometrical aspects of the system
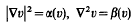 and applications to the nonlinear wave equation
and applications to the nonlinear wave equation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 247-256
-
- Article
-
- You have access
- Export citation
Nonlinear boundary value problems for elliptic systems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 257-272
-
- Article
-
- You have access
- Export citation
Exit times for elliptic diffusions and BMO
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 273-287
-
- Article
-
- You have access
- Export citation
Some examples of minimally degenerate Morse functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 289-293
-
- Article
-
- You have access
- Export citation
Application of Wynn's epsilon algorithm to periodic continued fractions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 295-299
-
- Article
-
- You have access
- Export citation
Explicit expressions for Sturm-Liouville operator problems
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 301-309
-
- Article
-
- You have access
- Export citation
Geometry relevant to the binary quintic
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 311-321
-
- Article
-
- You have access
- Export citation
Corrigenda: Inverse multi-parameter eigenvalue problems for matrices II
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 323
-
- Article
-
- You have access
- Export citation
Book Reviews
J. H. Conway, R. T. Curtis, S. P. Norton, R. A. Parker and R. A. Wilson, ATLAS of finite groups: maximal subgroups and ordinary characters for simple groups (Oxford University Press, 1985), xxxiii + 252 pp., £35.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 325
-
- Article
-
- You have access
- Export citation
H. A. Priestley, Introduction to complex analysis (Oxford University Press, 1985), 197 pp., £8.50.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 325-326
-
- Article
-
- You have access
- Export citation
M. Rosenblum and J. Rovnyak, Hardy classes and operator theory (Oxford University Press, USA, 1985), xii + 161 pp., £37.50.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 326-327
-
- Article
-
- You have access
- Export citation
J. R. Weeks, The shape of space: how to visualize surfaces and three-dimensional manifolds (Pure and Applied Mathematics Vol. 96, Marcel Dekker, New York, 1985), x + 324 pp., $59.50.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 327
-
- Article
-
- You have access
- Export citation
E. Grosswald, Representations of integers as sums of squares (Springer-Verlag, 1985) 251 pp., DM 148.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 327-329
-
- Article
-
- You have access
- Export citation
B. Bollobás, Random graphs (London Mathematical Society Monographs, Academic Press, London, 1985), 447 pp., £52 cloth, £27 paper.
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 329
-
- Article
-
- You have access
- Export citation

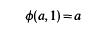
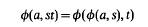
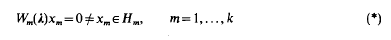
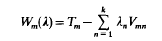
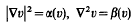 and applications to the nonlinear wave equation
and applications to the nonlinear wave equation

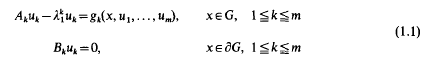
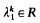 is such that the problem
is such that the problem
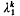 is the first eigenvalue associated with
is the first eigenvalue associated with