Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-11T17:32:26.742Z Has data issue: false hasContentIssue false
  • English
  • Français

Divisible S-systems and R-modules

Published online by Cambridge University Press:  20 January 2009

Victoria Gould
Victoria Gould
Affiliation:
School of Mathematics, University of Bristol, University Walk, Bristol BS8 1TW, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this paper S will denote a given monoid and R a given ring with unity. A set A is a right S-system if there is a map φ:A × S→A satisfying

and

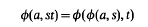
for any element a of A and any elements s, t of S. For φ(a, s) we write as and we refer to right S-systems simply as S-systems. One has the obvious definitions of an S-subsystem, an S-homomorphism and a congruence on an S-system. The reader ispresumed to be familiar with the basic definitions concerning right R-modules over R. As with S-systems we will refer to right R-modules just as R-modules.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 30 , Issue 2 , June 1987 , pp. 187 - 200
Copyright
Copyright © Edinburgh Mathematical Society 1987

References

REFERENCES

1.Anderson, F. W. and Fuller, K. R., Rings and categories of modules (Graduate Text in Mathematics, Springer-Verlag, Berlin-Heidelberg-New York, 1974).CrossRefGoogle Scholar
2.Damiano, R. F., Coflat rings and modules, Pacific J. Math. 81 (1979), 349–369.CrossRefGoogle Scholar
3.Dorofeeva, M. P., Hereditary and semi-hereditary monoids, Semigroup Forum 4 (1972), 301–311.CrossRefGoogle Scholar
4.Fountain, J. B., Completely right injective semigroups, Proc. London Math. Soc. 27 (1974), 28–44.CrossRefGoogle Scholar
5.Gould, V. A. R., The characterisation of monoids by properties of their S-systems, Semigroup Forum 32 (1985), 251–265.CrossRefGoogle Scholar
6.U., Knauer and Petrich, M., The characterisation of monoids by torsion-free flat, projective and free acts, Arch. Math. 36 (1981), 289–294.Google Scholar
7.Luedeman, J. K. and Mcmorris, F. R., Semigroups for which every totally irreducible S-system is injective, preprint.Google Scholar
8.Ming, R., On injective and p-injective modules, Riv. Mat. Univ. Parma 7 (1981), 187–197.Google Scholar
9.Ming, R., On (von Neumann) regular rings, Proc. Edinburgh Math. Soc. 19 (1974), 89–91.CrossRefGoogle Scholar
10.Normak, P., Purity in the category of M-sets, Semigroup Forum 20 (1980), 157–170.CrossRefGoogle Scholar