Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-16T17:59:41.219Z Has data issue: false hasContentIssue false
  • English
  • Français

Explicit expressions for Sturm-Liouville operator problems

Published online by Cambridge University Press:  20 January 2009

Lucas Jodar
Lucas Jodar
Affiliation:
Department of Applied Mathematics, Polytechnical University of Valencia, P.O. Box 22. 012, Valencia, Spain
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this paper H will denote a complex separable Hilbert space and L(H) denotes the algebra of all bounded linear operators on H. If T lies in L(H), its spectrum σ(T) is the set of all complex numbers z such zI–T is not invertible in L(H) and its compression spectrum σcomp(T) is the set of all complex numbers z such that the range (zI-T)(H) is not dense in H ([3, p. 240]). This paper is concerned with the Sturm–Liouville operator problem

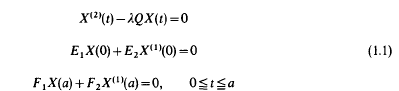
where λ is a complex parameter and X(t), Q, Ei, Fi for i = l,2, and t∈[0,a], are bounded operators in L(H). For the scalar case, the classical Sturm-Liouville theory yields a complete solution of the problem, see [4], and [7]. For the finite-dimensional case, second order operator differential equations are important in the theory of damped oscillatory systems and vibrational systems ([2, 6]). Infinite-dimensional differential equations occur frequently in the theory of stochastic processes, the degradation of polymers, infinite ladder network theory in engineering [1, 17], denumerable Markov chains, and moment problems [10, 20]. Sturm-Liouville operator problems have been studied by several authors and with several techniques ([12, 13, 14, 15, 16]).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 30 , Issue 2 , June 1987 , pp. 301 - 309
Copyright
Copyright © Edinburgh Mathematical Society 1987

References

REFERENCES

1.Arley, N. and Borchsenius, V., On the theory of infinite-systems of differential equations and their application to the theory of stochastic processes and the perturbation theory of quantum mechanics, Acta Math. 76 (1944), 261–322.Google Scholar
2.Bart, H., Kaashoek, M. A. and Lerer, L., Review of Matrix Polynomials, by Gohberg, I., Lancaster, P. and Rodman, L., Linear Algebra Appl. 64 (1985), 267–272.Google Scholar
3.Berberian, S. K., Lectures on Functional Analysis and Operator Theory (Springer-Verlag, 1974).Google Scholar
4.Coddington, E. A. and Levinson, N., Theory of Ordinary Differential Equations (MacGraw-Hill, 1955).Google Scholar
5.Dunford, N. and Schwartz, J., Linear Operators I (Interscience, 1957).Google Scholar
6.Gohberg, I., P., Lancaster and Rodman, L., Matrix Polynomials (Academic Press, 1982).Google Scholar
7.Ince, E. L., Ordinary Differential Equations (Dover, 1927).Google Scholar
8.Jodar, L., Boundary value problems for second order operator differential equations, Linear Algebra and Appl., to appear.CrossRefGoogle Scholar
9.Jodar, L., Boundary problems for Riccati and Lyapunov equations, Proc. Edinburgh Math. Soc. 29(1986), 15–21.CrossRefGoogle Scholar
10.Kemeny, J. G., Snell, J. L. and Knapp, A. W., Denumerable Markov Chains (Van Nostrand, Princeton).CrossRefGoogle Scholar
11.Krein, S. G., Linear differential equations in Banach spaces, Trans. Math. Monographs 29 (1971).Google Scholar
12.Misnaevskii, P. A., On the Green's function and the asymptotic behavior of eigenvalues of Sturm-Liouville operator problem, Soviet Math. Dokl. 13 (1972), 465–469.Google Scholar
13.Misnaevskii, P. A., On the spectral theory for the Sturm-Liouville equation with operator coefficient, Math. V.S.S.R. Izv. 10 (1976), 145–180.Google Scholar
14.Milhailec, V. A., The solvability and completeness of the system of eigenfunctions and associated functions of nonselfadjoint boundary value problems for a Sturm-Liouville operator equation, Soviet Math. Dokl. 15 (1974), 1327–1330.Google Scholar
15.Murtazin, H. H., On the point spectrum of a class of differential operator, Soviet Math. Dokl. 15(1974), 1812–1814.Google Scholar
16.Murtazin, H. H., On nonisolated points of the spectrum of eliptic operators, Math. U.S.S.R. Izv. 10(1976), 393–411.CrossRefGoogle Scholar
17.Oguztorelli, M. N., On infinite systems of differential equations occurring in the degradations of polymers, Utilitas Math. 1 (1972), 141–155.Google Scholar
18.Rodman, L., On factorization of operator polynomials and analytic operator functions, Rocky Mountain J. Math., to appear.Google Scholar
19.Shields, A. L., Weighted Shift Operators and Analytic Function Theory (Math. Surveys No. 13, C. Pearcy, Ed., Amer. Math. Soc, 1974).Google Scholar
20.Steinberg, S., Infinite systems of ordinary differential equations with unbounded coefficients and moment problems, J. Math. Anal. Appl. 41 (1973), 685–694.CrossRefGoogle Scholar