Research Article
A Note on Trace-Differentiation and the Ω-operator
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-4
-
- Article
-
- You have access
- Export citation
Matrix Differentiation of S-Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 5-10
-
- Article
-
- You have access
- Export citation
Note on γ-Matrices Efficient at an Isolated Point
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 11-12
-
- Article
-
- You have access
- Export citation
Theorems Relating to Quadratic Forms and their Discriminant Matrices
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 13-15
-
- Article
-
- You have access
- Export citation
On a Set of Conform-Invariant Equations of the Gravitational Field
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 16-20
-
- Article
-
- You have access
- Export citation
On a Certain Matrix Product with Specified Latent Roots
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 21-24
-
- Article
-
- You have access
- Export citation
On the Φ-Invariant of Two Quadrics
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 25-36
-
- Article
-
- You have access
- Export citation
On Symmetric, Orthogonal, and Skew-Symmetric Matrices
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 37-44
-
- Article
-
- You have access
- Export citation
Some Remarks on Uniform Convergence
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 45-52
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 10 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PEM volume 10 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation


 , Σλ
, Σλ
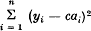 be given; introduce, for
be given; introduce, for 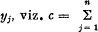 and obtain
and obtain
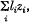 where
where 

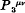 is a linear combination of
is a linear combination of 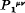 and
and 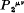 , i.e. of the Hamiltonian derivatives of
, i.e. of the Hamiltonian derivatives of 