No CrossRef data available.
Article contents
Theorems Relating to Quadratic Forms and their Discriminant Matrices
Published online by Cambridge University Press: 20 January 2009
Extract
In a paper read before the Research Branch of the Royal Statistical Society (Ref. 1, p. 150) the following case was considered:
Let the expression 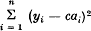 be given; introduce, for c, a linear form in
be given; introduce, for c, a linear form in 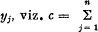 and obtain
and obtain

If the yi are sample values from a normal population with unit variance, then it is known (Ref. 2) that (1) is distributed as 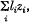 where zi varies as chi-squared with one degree of freedom and the li are the latent roots of the matrix of the quadratic form. If these latent roots are f times unity and n—f times zero, then this reduces to a chi-squared distribution with f degrees of freedom.
where zi varies as chi-squared with one degree of freedom and the li are the latent roots of the matrix of the quadratic form. If these latent roots are f times unity and n—f times zero, then this reduces to a chi-squared distribution with f degrees of freedom.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 10 , Issue 1 , January 1953 , pp. 13 - 15
- Copyright
- Copyright © Edinburgh Mathematical Society 1953


