Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Buchdahl, H A
1983.
Nonlinear Lagrangians and pp waves.
Journal of Physics A: Mathematical and General,
Vol. 16,
Issue. 7,
p.
1441.
Riegert, Ronald J.
1984.
Birkhoff's Theorem in Conformal Gravity.
Physical Review Letters,
Vol. 53,
Issue. 4,
p.
315.
SCHMIDT, HANS-JÜRGEN
2007.
FOURTH ORDER GRAVITY: EQUATIONS, HISTORY, AND APPLICATIONS TO COSMOLOGY.
International Journal of Geometric Methods in Modern Physics,
Vol. 04,
Issue. 02,
p.
209.
Lanahan-Tremblay, Nicolas
and
Faraoni, Valerio
2007.
The Cauchy problem of
f
(
R
) gravity
.
Classical and Quantum Gravity,
Vol. 24,
Issue. 22,
p.
5667.
Pradhan, Parthapratim
2018.
P–V criticality of conformal gravity holography in four dimensions.
Modern Physics Letters A,
Vol. 33,
Issue. 05,
p.
1850030.
Momennia, Mehrab
and
Hendi, Seyed Hossein
2019.
Near-extremal black holes in Weyl gravity: Quasinormal modes and geodesic instability.
Physical Review D,
Vol. 99,
Issue. 12,
Momennia, Mehrab
and
Hendi, Seyed Hossein
2020.
Quasinormal modes of black holes in Weyl gravity: electromagnetic and gravitational perturbations.
The European Physical Journal C,
Vol. 80,
Issue. 6,
Hervik, Sigbjørn
and
Ortaggio, Marcello
2020.
Universal black holes.
Journal of High Energy Physics,
Vol. 2020,
Issue. 2,
Momennia, Mehrab
Hendi, Seyed Hossein
and
Soltani Bidgoli, Fatemeh
2021.
Stability and quasinormal modes of black holes in conformal Weyl gravity.
Physics Letters B,
Vol. 813,
Issue. ,
p.
136028.
Ortaggio, Marcello
2022.
Einstein–Maxwell fields as solutions of higher-order theories.
The European Physical Journal C,
Vol. 82,
Issue. 11,
Pravdová, Alena
Pravda, Vojtěch
and
Ortaggio, Marcello
2023.
Topological black holes in higher derivative gravity.
The European Physical Journal C,
Vol. 83,
Issue. 2,
Lecian, Orchidea Maria
2024.
Generalized Schwarzschild Spacetimes with a Linear Term and a Cosmological Constant.
Universe,
Vol. 10,
Issue. 11,
p.
408.
Pravda, Vojtěch
Pravdová, Alena
and
Turner, George
2024.
Charged black holes in quadratic gravity.
Physical Review D,
Vol. 110,
Issue. 4,


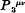 is a linear combination of
is a linear combination of 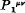 and
and 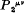 , i.e. of the Hamiltonian derivatives of K1 and K2. In fact
, i.e. of the Hamiltonian derivatives of K1 and K2. In fact