Research Article
On a Generalisation of the Laplace Transformation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 53-55
-
- Article
-
- You have access
- Export citation
On Equivalent Truth-Tables of Many-Valued Logics
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 56-61
-
- Article
-
- You have access
- Export citation
Integral Functions with Gap Power Series
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 62-70
-
- Article
-
- You have access
- Export citation
Integral Equations Satisfied by Lamé-Wangerin Functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 71-75
-
- Article
-
- You have access
- Export citation
Congruences on a Distributive Lattice
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 76-77
-
- Article
-
- You have access
- Export citation
A Determinantal Expansion for a Class of Definite Integral
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 78-91
-
- Article
-
- You have access
- Export citation
Diffraction by a Half-Plane
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 92-99
-
- Article
-
- You have access
- Export citation
A Note about Functions in Lip α
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 100
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 10 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PEM volume 10 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation







 This expansion may be expressed as a determinantal quotient or Schweinsian series. In the present paper we state more general terms under which the expansion holds and consider the case when the limits of integration are infinite and the weight function of the form
This expansion may be expressed as a determinantal quotient or Schweinsian series. In the present paper we state more general terms under which the expansion holds and consider the case when the limits of integration are infinite and the weight function of the form  In particular we giye expansions for
In particular we giye expansions for  the Psi function, and
the Psi function, and  where
where 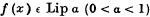 is that σ
is that σ