Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T03:01:01.960Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Generalisation of the Laplace Transformation

Published online by Cambridge University Press:  20 January 2009

A. Erdélyi
A. Erdélyi
Affiliation:
California Institute of Technology, Pasadena 4, California.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

On reading a recent paper by R. S. Varma (Varma 1949) I recalled that in May 1942 I investigated an integral transformation which is very similar to Varma's. Varma has

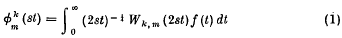
and points out that this reduces to a Laplace integral for k = ¼, m = ± ¼. Instead of (1), one could consider the integral

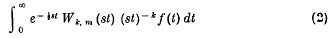
which was introduced by C. S. Meijer (Meijer 1940 b); this integral reduces to a Laplace integral whenever k = m + ½. Now, apart from comparatively unimportant factors, the nucleus of (2) is a fractional derivative or integral, as the case may be, of e−st, and on carrying out a fractional integration by parts, it appears that (2) is essentially the Laplace transform of a fractional integral or derivative of f. Thus, the whole theory of the transformation (2), including inversion formulae, representation theorems, etc., can be deduced from the well-known theory of the Laplace transformation. It is not quite clear that a similar reduction is possible for (1), although it is certainly possible when k = 0.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 10 , Issue 2 , December 1954 , pp. 53 - 55
Copyright
Copyright © Edinburgh Mathematical Society 1954

References

REFERENCES

Boas, R. P., 1942a. Proc. Nat. Ac. Sci. 28, 21–24.CrossRefGoogle Scholar
Boas, R. P., 1942b. Bull. American Math. Soc. 48, 286–294.CrossRefGoogle Scholar
Erdélyi, A., 1940. Quart. J. Math. (Oxford) 11, 293–303.Google Scholar
Kober, H., 1940. Quart. J. Math. (Oxford) 11, 193–211.Google Scholar
Kober, H., 1941. Trans. American Math. Soc. 50, 160–174.Google Scholar
Meijer, C. S., 1940a. Proc. Amsterdam Ak. Wet. 43, 599–608 and 702–711.Google Scholar
Meijer, C. S. 1940b. Proc. Amsterdam Ah. Wet. 44, 727–737 and 831–839.Google Scholar
Varma, R. S., 1949. Proc. Edinburgh Math. Soc. (2) 8, 126–127.CrossRefGoogle Scholar