Research Article
Multipliers of invariant subspaces in the bidisc
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 193-199
-
- Article
-
- You have access
- Export citation
Group rings whose torsion units form a subgroup*
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 201-205
-
- Article
-
- You have access
- Export citation
(p, r)-convex functions on vector lattices
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 207-226
-
- Article
-
- You have access
- Export citation
Some results on symmetrically-presented groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 227-237
-
- Article
-
- You have access
- Export citation
A simple proof of Arazy's theorem
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 239-242
-
- Article
-
- You have access
- Export citation
Lp-convergence of a certain class of product martingales
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 243-254
-
- Article
-
- You have access
- Export citation
On rooted properties of complex analytic systems*
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 255-270
-
- Article
-
- You have access
- Export citation
Multiresolution and wavelets
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 271-300
-
- Article
-
- You have access
- Export citation
The asymptotic distribution of the eigenvalues of multiparameter Sturm–Liouville systems II
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 301-316
-
- Article
-
- You have access
- Export citation
Unions of Cockcroft two-complexes
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 317-324
-
- Article
-
- You have access
- Export citation
Finitely-generated solutions of certain integral equations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 325-345
-
- Article
-
- You have access
- Export citation
Stability of Gelfand–Kirillov dimension for rings with the strong second layer condition
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 347-354
-
- Article
-
- You have access
- Export citation
Linear metric spaces and analytic sets
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 355-358
-
- Article
-
- You have access
- Export citation
Other
Sir Edmund Whittaker Memorial Prize
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 359-360
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 37 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back matter
PEM volume 37 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 January 2009, p. b1
-
- Article
-
- You have access
- Export citation

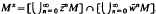 . Then
. Then 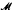 (M) = {ø ∈ L ∞: ø M ⊆
(M) = {ø ∈ L ∞: ø M ⊆ 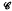
 (
(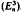 .
.