No CrossRef data available.
Published online by Cambridge University Press: 20 January 2009
This paper is devoted to the study of rooted properties of phase surfaces defined by complex analytic systems. We first obtain the Rooted Theorem of Analytic Systems. Then we prove the Generalized Strong Rooted Theorem of  (m ≧ 2), which implying the Strong Rooted Theorem of a Class of
(m ≧ 2), which implying the Strong Rooted Theorem of a Class of 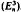 .
.