Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-20T04:42:52.655Z Has data issue: false hasContentIssue false
  • English
  • Français

Multipliers of invariant subspaces in the bidisc

Published online by Cambridge University Press:  20 January 2009

Takahiko Nakazi
Takahiko Nakazi
Affiliation:
Department of Mathematics Faculty of ScienceHokkaido UniversitySapporo 060, Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any nonzero invariant subspace M in H2(T2), set 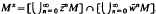. Then Mx is also an invariant subspace of H2(T2) that contains M. If M is of finite codimension in H2(T2) then Mx = H2(T2) and if M = qH2(T2) for some inner function q then Mx = M. In this paper invariant subspaces with Mx = M are studied. If M = q1H2(T2) ∩ q2H2(T2) and q1, q2 are inner functions then Mx = M. However in general this invariant subspace may not be of the form: qH2(T2) for some inner function q. Put 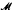(M) = {ø ∈ L ∞: ø M ⊆ H2(T2)}; then 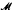(M) is described and 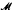(M) = 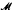(Mx) is shown. This is the set of all multipliers of M in the title. A necessary and sufficient condition for 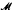(M) = H∞(T2) is given. It is noted that the kernel of a Hankel operator is an invariant subspace M with Mx = M. The argument applies to the polydisc case.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 37 , Issue 2 , June 1994 , pp. 193 - 199
Copyright
Copyright © Edinburgh Mathematical Society 1994

References

REFERENCES

1.Ahern, P. R. and Clark, D. N., Invariant subspaces and analytic continuation in several variables. J. Math. Mech 19 (1970), 963–969.Google Scholar
2.Agrawal, O. P., Clark, D. N. and Douglas, R. G., Invariant subspaces in the polydisk, Pacific J. Math. 121 (1986), 1–11.Google Scholar
3.Douglas, R. G. and Yan, K., On the rigidity of Hardy submodules, Integral Equations Operator Theory 13 (1990), 350–363.CrossRefGoogle Scholar
4.Hoffman, K., Banach Spaces of Analytic Functions. (Prentice-Hall, 1962).Google Scholar
5.Izuchi, K., Unitary equivalence of invariant subspaces in the polydisk, Pacific J. Math. 130 1987), 351–358.Google Scholar
6.Nakazi, T., Nonmaximal weak-* Dirichlet algebra, Hokkaido Math. J. 5 (1976), 88–96.Google Scholar
7.Nakazi, T., Invariant subspaces of weak-* Dirichlet algebras. Pacific J. Math 69 (1977), 151–167.CrossRefGoogle Scholar
8.Nakazi, T., Certain invariant subspaces of H2 and L2 on a bidisc, Canad. J. Math. 40 (1988), 1272–1280.CrossRefGoogle Scholar
9.Nakazi, T., Invariant subspaces in the bidisc and commutators, J. Austral. Math. Soc, to appear.Google Scholar
10.Nakazi, T., Homogeneous polynomials and invariant subspaces in the polydiscs. Arch. Math. 58 (1992). 56–63.CrossRefGoogle Scholar
11.Rudin, W., Invariant subspaces of H2 on a torus, J. Funct. Anal. 61 (1985), 378–384.Google Scholar