Research Article
A hybrid mean value of the inversion of L-functions and general quadratic Gauss sums*
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-15
-
- Article
-
- You have access
- Export citation
Boundedness of homogeneous fractional integrals on Lp for N/α ≤ P ≤ ∞
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 17-33
-
- Article
-
- You have access
- Export citation
Two meromorphic functions sharing five small functions in the sense of Ēk)(β, f) = Ēk)(β, g)*
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 35-54
-
- Article
-
- You have access
- Export citation
Sextactic points on a simple closed curve
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 55-94
-
- Article
-
- You have access
- Export citation
On the average of central values of symmetric square L-functions in weight aspect
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 95-100
-
- Article
-
- You have access
- Export citation
On the number of moduli of extendable canonical curves
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 101-115
-
- Article
-
- You have access
- Export citation
On classification of ℚ-fano 3-folds of Gorenstein index 2. I
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 117-155
-
- Article
-
- You have access
- Export citation
On classification of ℚ-fano 3-folds of Gorenstein index 2. II
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 157-216
-
- Article
-
- You have access
- Export citation
On the dimension and multiplicity of local cohomology modules
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 217-233
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 167 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f3
-
- Article
-
- You have access
- Export citation

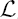
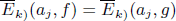 (
(