Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T23:44:49.925Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundedness of homogeneous fractional integrals on Lp for N/α ≤ P ≤ ∞

Published online by Cambridge University Press:  22 January 2016

Yong Ding  and
Shanzhen Lu
Yong Ding
Affiliation:
Department of Mathematics, Beijing Normal University, Beijing, 100875, P.R.of China, [email protected]
Shanzhen Lu
Affiliation:
Department of Mathematics, Beijing Normal University, Beijing, 100875, P.R.of China. [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study the map properties of the homogeneous fractional integral operator TΩ, α on Lp(ℝn) for n/α ≤ p ≤ ∞.

We prove that if Ω satisfies some smoothness conditions on Sn−1 then TΩ, α is bounded from Ln/α(ℝn) to BMO(ℝn), and from Lp(ℝn) (n/α < p ≤ ∞) to a class of the Campanato spaces 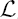l, λ (ℝn), respectively. As the corollary of the results above, we show that when Ω satisfies some smoothness conditions on Sn−1 the homogeneous fractional integral operator TΩ, α is also bounded from Hp(ℝn) (n/(n + α) ≤ p ≤ 1) to Lq(ℝn) for 1/q = 1/p-α/n. The results are the extensions of Stein-Weiss (for p = 1) and Taibleson-Weiss’s (for n/(n + α) ≤ p < 1) results on the boundedness of the Riesz potential operator Iα on the Hardy spaces Hp(ℝn).

Keywords

42B2047G10
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 167 , 2002 , pp. 17 - 33
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2002

References

[1] Chanillo, S., Watson, D. and Wheeden, R. L., Some integral and maximal operators related to star-like, Studia Math., 107 (1993), 223–255.CrossRefGoogle Scholar
[2] Ding, Y. and Lu, S. Z., Weighted norm inequalities for fractional integral operators with rough kernel, Canad. J. Math., 50 (1998), 29–39.Google Scholar
[3] Ding, Y. and Lu, S. Z., The Lp1 × Lp2 × … × Lpk boundedness for some rough operators, J. Math. Anal. Appl., 203 (1996), 166–186.Google Scholar
[4] Ding, Y., Weak type bounds for a class of rough operators with power weights, Proc. Amer. Math. Soc, 125 (1997), 2939–2942.CrossRefGoogle Scholar
[5] Kurtz, D. and Wheeden, R. L., Results on weighted norm inequalities for multipliers, Trans. Amer. Math. Soc, 255 (1979), 343–362.Google Scholar
[6] Lu, S. Z., Four lectures on real Hp spaces, World Scientific Publishing Co. Pte. Ltd., 1995.CrossRefGoogle Scholar
[7] Muckenhoupt, B. and Wheeden, R. L., Weighted norm inequalities for singular and fractional integrals, Trans. Amer. Math. Soc, 161 (1971), 249–258.CrossRefGoogle Scholar
[8] Muckenhoupt, B. and Wheeden, R. L., Weighted norm inequalities for fractional integrals, Trans. Amer. Math. Soc, 192 (1974), 261–274.Google Scholar
[9] Peeter, J., On the theory of p,λ spaces, J. Funct. Anal., 4 (1969), 71–87.Google Scholar
[10] Stein, E. M., Harmonic Analysis: Real-Variable Methods, Orthogonality, and Ocillatory Integrals, Princeton Univ. Press, Princeton, N.J., 1993.Google Scholar
[11] Stein, E. M. and Weiss, G., On the theory of harmonic functions of several variables I: The theory of Hp spaces, Acta Math., 103 (1960), 25–62.Google Scholar
[12] Taibleson, M. H. and Weiss, G., The molecular characterization of certain Hardy spaces, Astérisque, 77 (1980), 67–149.Google Scholar