We prove the deformation invariance of Kodaira dimension and of certain plurigenera and the existence of canonical models for log surfaces which are smooth over an integral Noetherian scheme S$S$.

We study a rough differential equation driven by fractional Brownian motion with Hurst parameter H$H$(1/4<H\leqslant 1/2)$(1/4<H\leqslant 1/2)$. Under Hörmander’s condition on the coefficient vector fields, the solution has a smooth density for each fixed time. Using Watanabe’s distributional Malliavin calculus, we obtain a short time full asymptotic expansion of the density under quite natural assumptions. Our main result can be regarded as a “fractional version” of Ben Arous’ famous work on the off-diagonal asymptotics.

This paper stems from the observation (arising from work of Delzant) that “most” Kähler groups G$G$ virtually algebraically fiber, that is, admit a finite index subgroup that maps onto \mathbb{Z}$\mathbb{Z}$ with finitely generated kernel. For the remaining ones, the Albanese dimension of all finite index subgroups is at most one, that is, they have virtual Albanese dimension va(G)\leqslant 1$va(G)\leqslant 1$. We show that the existence of algebraic fibrations has implications in the study of coherence and higher BNSR invariants of the fundamental group of aspherical Kähler surfaces. The class of Kähler groups with va(G)=1$va(G)=1$ includes virtual surface groups. Further examples exist; nonetheless, they exhibit a strong relation with surface groups. In fact, we show that the Green–Lazarsfeld sets of groups with va(G)=1$va(G)=1$ (virtually) coincide with those of surface groups, and furthermore that the only virtually RFRS groups with va(G)=1$va(G)=1$ are virtually surface groups.

We consider the space X=\bigwedge ^{3}\mathbb{C}^{6}$X=\bigwedge ^{3}\mathbb{C}^{6}$ of alternating senary 3-tensors, equipped with the natural action of the group \operatorname{GL}_{6}$\operatorname{GL}_{6}$ of invertible linear transformations of \mathbb{C}^{6}$\mathbb{C}^{6}$. We describe explicitly the category of \operatorname{GL}_{6}$\operatorname{GL}_{6}$-equivariant coherent {\mathcal{D}}_{X}${\mathcal{D}}_{X}$-modules as the category of representations of a quiver with relations, which has finite representation type. We give a construction of the six simple equivariant {\mathcal{D}}_{X}${\mathcal{D}}_{X}$-modules and give formulas for the characters of their underlying \operatorname{GL}_{6}$\operatorname{GL}_{6}$-structures. We describe the (iterated) local cohomology groups with supports given by orbit closures, determining, in particular, the Lyubeznik numbers associated to the orbit closures.

A Vaisman manifold is a special kind of locally conformally Kähler manifold, which is closely related to a Sasaki manifold. In this paper, we show a basic structure theorem of simply connected homogeneous Sasaki and Vaisman manifolds of unimodular Lie groups, up to holomorphic isometry. For the case of unimodular Lie groups, we obtain a complete classification of simply connected Sasaki and Vaisman unimodular Lie groups, up to modification.

Let R$R$ be a ring and T$T$ be a good Wakamatsu-tilting module with S=\text{End}(T_{R})^{op}$S=\text{End}(T_{R})^{op}$. We prove that T$T$ induces an equivalence between stable repetitive categories of R$R$ and S$S$ (i.e., stable module categories of repetitive algebras \hat{R}$\hat{R}$ and {\hat{S}}${\hat{S}}$). This shows that good Wakamatsu-tilting modules seem to behave in Morita theory of stable repetitive categories as that tilting modules of finite projective dimension behave in Morita theory of derived categories.

We first characterize the automorphism groups of Hodge structures of cubic threefolds and cubic fourfolds. Then we determine for some complex projective manifolds of small dimension (cubic surfaces, cubic threefolds, and nonhyperelliptic curves of genus 3 or 4), the action of their automorphism groups on Hodge structures of associated cyclic covers, and thus confirm conjectures made by Kudla and Rapoport in (Pacific J. Math. 260(2) (2012), 565–581).

Let \mathfrak{o}$\mathfrak{o}$ be a complete discrete valuation ring of mixed characteristic 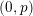(0,p)$(0,p)$ and 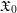\mathfrak{X}_{0}$\mathfrak{X}_{0}$ a smooth formal \mathfrak{o}$\mathfrak{o}$-scheme. Let 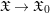\mathfrak{X}\rightarrow \mathfrak{X}_{0}$\mathfrak{X}\rightarrow \mathfrak{X}_{0}$ be an admissible blow-up. In the first part, we introduce sheaves of differential operators 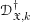\mathscr{D}_{\mathfrak{X},k}^{\dagger }$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$ on 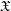\mathfrak{X}$\mathfrak{X}$, for every sufficiently large positive integer 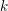k$k$, generalizing Berthelot’s arithmetic differential operators on the smooth formal scheme 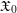\mathfrak{X}_{0}$\mathfrak{X}_{0}$. The coherence of these sheaves and several other basic properties are proven. In the second part, we study the projective limit sheaf 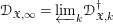\mathscr{D}_{\mathfrak{X},\infty }=\mathop{\varprojlim }\nolimits_{k}\mathscr{D}_{\mathfrak{X},k}^{\dagger }$\mathscr{D}_{\mathfrak{X},\infty }=\mathop{\varprojlim }\nolimits_{k}\mathscr{D}_{\mathfrak{X},k}^{\dagger }$ and introduce its abelian category of coadmissible modules. The inductive limit of the sheaves 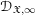\mathscr{D}_{\mathfrak{X},\infty }$\mathscr{D}_{\mathfrak{X},\infty }$, over all admissible blow-ups 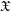\mathfrak{X}$\mathfrak{X}$, is a sheaf 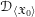\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$ on the Zariski–Riemann space of 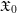\mathfrak{X}_{0}$\mathfrak{X}_{0}$, which gives rise to an abelian category of coadmissible modules. Analogues of Theorems A and B are shown to hold in each of these settings, that is, for 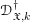\mathscr{D}_{\mathfrak{X},k}^{\dagger }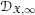$\mathscr{D}_{\mathfrak{X},k}^{\dagger }$, \mathscr{D}_{\mathfrak{X},\infty }$\mathscr{D}_{\mathfrak{X},\infty }$, and 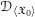\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$\mathscr{D}_{\langle \mathfrak{X}_{0}\rangle }$.

We show that if a link L$L$ has a closed n$n$-braid representative admitting a nondegenerate exchange move, an exchange move that does not obviously preserve the conjugacy class, L$L$ has infinitely many nonconjugate closed n$n$-braid representatives.

We consider a family M_{t}^{3}$M_{t}^{3}$, with t>1$t>1$, of real hypersurfaces in a complex affine three-dimensional quadric arising in connection with the classification of homogeneous compact simply connected real-analytic hypersurfaces in \mathbb{C}^{n}$\mathbb{C}^{n}$ due to Morimoto and Nagano. To finalize their classification, one needs to resolve the problem of the Cauchy–Riemann (CR)-embeddability of M_{t}^{3}$M_{t}^{3}$ in \mathbb{C}^{3}$\mathbb{C}^{3}$. In our earlier article, we showed that M_{t}^{3}$M_{t}^{3}$ is CR-embeddable in \mathbb{C}^{3}$\mathbb{C}^{3}$ for all 1<t<\sqrt{(2+\sqrt{2})/3}$1<t<\sqrt{(2+\sqrt{2})/3}$. In the present paper, we prove that M_{t}^{3}$M_{t}^{3}$ can be immersed in \mathbb{C}^{3}$\mathbb{C}^{3}$ for every t>1$t>1$ by means of a polynomial map. In addition, one of the immersions that we construct helps simplify the proof of the above CR-embeddability theorem and extend it to the larger parameter range 1<t<\sqrt{5}/2$1<t<\sqrt{5}/2$.

We develop the notion of renormalized energy in Cauchy–Riemann (CR) geometry for maps from a strictly pseudoconvex pseudo-Hermitian manifold to a Riemannian manifold. This energy is a CR invariant functional whose critical points, which we call CR-harmonic maps, satisfy a CR covariant partial differential equation. The corresponding operator coincides on functions with the CR Paneitz operator.

We compute cones of effective cycles on some blowups of projective spaces in general sets of lines.

In this short note, we confirm a conjecture of Vasconcelos which states that the Rees algebra of any Artinian almost complete intersection monomial ideal is almost Cohen–Macaulay.

We study irreducible holomorphic symplectic manifolds deformation equivalent to Hilbert schemes of points on a K3$K3$ surface and admitting a non-symplectic involution. We classify the possible discriminant quadratic forms of the invariant and coinvariant lattice for the action of the involution on cohomology and explicitly describe the lattices in the cases where the invariant lattice has small rank. We also give a modular description of all d$d$-dimensional families of manifolds of K3^{[n]}$K3^{[n]}$-type with a non-symplectic involution for d\geqslant 19$d\geqslant 19$ and n\leqslant 5$n\leqslant 5$ and provide examples arising as moduli spaces of twisted sheaves on a K3$K3$ surface.

As was shown by a part of the authors, for a given (2,3,5)$(2,3,5)$-distribution D$D$ on a five-dimensional manifold Y$Y$, there is, locally, a Lagrangian cone structure C$C$ on another five-dimensional manifold X$X$ which consists of abnormal or singular paths of (Y,D)$(Y,D)$. We give a characterization of the class of Lagrangian cone structures corresponding to (2,3,5)$(2,3,5)$-distributions. Thus, we complete the duality between (2,3,5)$(2,3,5)$-distributions and Lagrangian cone structures via pseudo-product structures of type G_{2}$G_{2}$. A local example of nonflat perturbations of the global model of flat Lagrangian cone structure which corresponds to (2,3,5)$(2,3,5)$-distributions is given.

In this article, we study short exact sequences of finitary 2-representations of a weakly fiat 2-category. We provide a correspondence between such short exact sequences with fixed middle term and coidempotent subcoalgebras of a coalgebra 1-morphism defining this middle term. We additionally relate these to recollements of the underlying abelian 2-representations.