Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-11T16:19:05.978Z Has data issue: false hasContentIssue false
  • English
  • Français

EQUIVARIANT 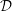${\mathcal{D}}$-MODULES ON ALTERNATING SENARY 3-TENSORS

Part of: (Co)homology theory Commutative algebra: Homological methods General commutative ring theory

Published online by Cambridge University Press:  29 November 2019

ANDRÁS C. LŐRINCZ  and
MICHAEL PERLMAN
ANDRÁS C. LŐRINCZ
Affiliation:
Max Planck Institute for Mathematics in the Sciences, Inselstrasse 22, Leipzig, Germany04103 email [email protected]
MICHAEL PERLMAN
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, IN46556 email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the space 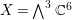$X=\bigwedge ^{3}\mathbb{C}^{6}$ of alternating senary 3-tensors, equipped with the natural action of the group 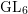$\operatorname{GL}_{6}$ of invertible linear transformations of 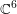$\mathbb{C}^{6}$. We describe explicitly the category of 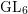$\operatorname{GL}_{6}$-equivariant coherent ${\mathcal{D}}_{X}$-modules as the category of representations of a quiver with relations, which has finite representation type. We give a construction of the six simple equivariant 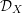${\mathcal{D}}_{X}$-modules and give formulas for the characters of their underlying 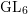$\operatorname{GL}_{6}$-structures. We describe the (iterated) local cohomology groups with supports given by orbit closures, determining, in particular, the Lyubeznik numbers associated to the orbit closures.

MSC classification

Primary: 14F10: Differentials and other special sheaves; D-modules; Bernstein-Sato ideals and polynomials 13D45: Local cohomology 13A50: Actions of groups on commutative rings; invariant theory
Type
Article
Information
Nagoya Mathematical Journal , Volume 243 , September 2021 , pp. 61 - 82
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Assem, I., Simson, D. and Skowroński, A., Elements of the Representation Theory of Associative Algebras. Vol. 1, London Mathematical Society Student Texts 65, Cambridge University Press, Cambridge, 2006.CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., The Magma algebra system. I. The user language, J. Symbolic Comput. 24(3–4) (1997), 235–265; Computational algebra and number theory (London, 1993).CrossRefGoogle Scholar
Brion, M., Invariants d’un sous-groupe unipotent maximal d’un groupe semi-simple, Ann. Inst. Fourier (Grenoble) 33(1) (1983), 1–27.Google Scholar
García López, R. and Sabbah, C., Topological computation of local cohomology multiplicities, Collect. Math. 49(2–3) (1998), 317–324; Dedicated to the memory of Fernando Serrano, MR 1677136.Google Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics 52, Springer, New York-Heidelberg, 1977.CrossRefGoogle Scholar
Hotta, R., Takeuchi, K. and Tanisaki, T., D-Modules, Perverse Sheaves, and Representation Theory, Progress in Mathematics 236, Birkhäuser Boston, Inc., Boston, MA, 2008, Translated from the 1995 Japanese edition by Takeuchi.CrossRefGoogle Scholar
Igusa, J.-i., An Introduction to the Theory of Local Zeta Functions, AMS/IP Studies in Advanced Mathematics, 14, American Mathematical Society, Providence, RI, 2000, International Press, Cambridge, MA.Google Scholar
Kashiwara, M., D-Modules and Microlocal Calculus, Iwanami Series in Modern Mathematics; Translations of Mathematical Monographs 217, American Mathematical Society, Providence, RI, 2003.Google Scholar
Kimura, T., The b-functions and holonomy diagrams of irreducible regular prehomogeneous vector spaces, Nagoya Math. J. 85 (1982), 1–80.CrossRefGoogle Scholar
Knop, F. and Menzel, G., Duale Varietäten von Fahnenvarietäten, Comment. Math. Helv. 62(1) (1987), 38–61.CrossRefGoogle Scholar
Lőrincz, A., Decompositions of Bernstein–Sato polynomials and slices, Transform. Groups (2019), doi:10.1007/s00031-019-09526-7.Google Scholar
Landsberg, J. M. and Manivel, L., Series of Lie groups, Michigan Math. J. 52(2) (2004), 453–479.CrossRefGoogle Scholar
Lőrincz, A. C. and Raicu, C., Iterated local cohomology groups and Lyubeznik numbers for determinantal rings, 2018, arXiv:1805.08895.Google Scholar
Lőrincz, A. C., Raicu, C. and Weyman, J., Equivariant 𝓓-modules on binary cubic forms, Comm. Algebra 47 (2019), 2457–2487.10.1080/00927872.2018.1492590CrossRefGoogle Scholar
Lyubeznik, G., Singh, A. K. and Walther, U., Local cohomology modules supported at determinantal ideals, J. Eur. Math. Soc. (JEMS) 18(11) (2016), 2545–2578; MR 3562351.CrossRefGoogle Scholar
Lőrincz, A. C. and Walther, U., On categories of equivariant D-modules, Adv. Math. 351 (2019), 429–478.CrossRefGoogle Scholar
Lyubeznik, G., Finiteness properties of local cohomology modules (an application of D-modules to commutative algebra), Invent. Math. 113(1) (1993), 41–55.CrossRefGoogle Scholar
Manivel, L., Symmetric Functions, Schubert Polynomials and Degeneracy Loci, SMF/AMS Texts and Monographs 6, American Mathematical Society, Providence, RI, 2001, Société Mathématique de France, Paris, Translated from the 1998 French original by John R. Swallow, Cours Spécialisés [Specialized Courses], 3, MR 1852463.Google Scholar
MacPherson, R. and Vilonen, K., Elementary construction of perverse sheaves, Invent. Math. 84(2) (1986), 403–435.CrossRefGoogle Scholar
MacPherson, R. and Vilonen, K., Elementary construction of perverse sheaves, Invent. Math. 84 (1986), 403–435.CrossRefGoogle Scholar
Núñez Betancourt, L., Witt, E. E. and Zhang, W., A survey on the Lyubeznik numbers, Mexican mathematicians abroad: recent contributions (2016), 137–163.CrossRefGoogle Scholar
Ogus, A., Local cohomological dimension of algebraic varieties, Ann. of Math. (2) 98 (1973), 327–365; MR 506248.CrossRefGoogle Scholar
Perlman, M., Equivariant 𝓓-modules on 2 × 2 × 2 hypermatrices, J. Algebra (2018), to appear, arXiv:1809.00352.Google Scholar
Raicu, C., Characters of equivariant 𝓓-modules on spaces of matrices, Compos. Math. 152 (2016), 1935–1965.CrossRefGoogle Scholar
Raicu, C., Characters of equivariant 𝓓-modules on Veronese cones, Trans. Amer. Math. Soc. 369(3) (2017), 2087–2108.CrossRefGoogle Scholar
Raicu, C. and Weyman, J., Local cohomology with support in generic determinantal ideals, Algebra Number Theory 8(5) (2014), 1231–1257.CrossRefGoogle Scholar
Raicu, C. and Weyman, J., Local cohomology with support in ideals of symmetric minors and Pfaffians, J. Lond. Math. Soc. (2) 94(3) (2016), 709–725.CrossRefGoogle Scholar
Raicu, C., Weyman, J. and Witt, E., Local cohomology with support in ideals of maximal minors and sub-maximal Pfaffians, Adv. Math. 250 (2014), 596–610.CrossRefGoogle Scholar
Saito, M., On b-function, spectrum and rational singularity, Math. Ann. 295 (1993), 51–74.CrossRefGoogle Scholar
Sato, M. and Kimura, T., A classification of irreducible prehomogeneous vector spaces and their relative invariants, Nagoya Math. J. 65 (1977), 1–155.CrossRefGoogle Scholar
Switala, N., Lyubeznik numbers for nonsingular projective varieties, Bull. Lond. Math. Soc. 47(1) (2015), 1–6.CrossRefGoogle Scholar
Vilonen, K., Perverse sheaves and finite-dimensional algebras, Trans. Amer. Math. Soc. 341(2) (1994), 665–676.Google Scholar
Weyman, J., Cohomology of Vector Bundles and Syzygies, Cambridge Tracts in Mathematics 149, Cambridge University Press, Cambridge, 2003.CrossRefGoogle Scholar
Weyman, J., Calculating discriminants by higher direct images, Trans. Amer. Math. Soc. 343(1) (1994), 367–389.CrossRefGoogle Scholar