No CrossRef data available.
Published online by Cambridge University Press: 19 December 2019
We consider a family 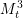 $M_{t}^{3}$, with
$M_{t}^{3}$, with 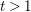 $t>1$, of real hypersurfaces in a complex affine three-dimensional quadric arising in connection with the classification of homogeneous compact simply connected real-analytic hypersurfaces in
$t>1$, of real hypersurfaces in a complex affine three-dimensional quadric arising in connection with the classification of homogeneous compact simply connected real-analytic hypersurfaces in 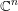 $\mathbb{C}^{n}$ due to Morimoto and Nagano. To finalize their classification, one needs to resolve the problem of the Cauchy–Riemann (CR)-embeddability of
$\mathbb{C}^{n}$ due to Morimoto and Nagano. To finalize their classification, one needs to resolve the problem of the Cauchy–Riemann (CR)-embeddability of 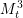 $M_{t}^{3}$ in
$M_{t}^{3}$ in 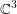 $\mathbb{C}^{3}$. In our earlier article, we showed that
$\mathbb{C}^{3}$. In our earlier article, we showed that 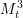 $M_{t}^{3}$ is CR-embeddable in
$M_{t}^{3}$ is CR-embeddable in 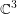 $\mathbb{C}^{3}$ for all
$\mathbb{C}^{3}$ for all 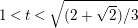 $1<t<\sqrt{(2+\sqrt{2})/3}$. In the present paper, we prove that
$1<t<\sqrt{(2+\sqrt{2})/3}$. In the present paper, we prove that 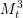 $M_{t}^{3}$ can be immersed in
$M_{t}^{3}$ can be immersed in 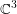 $\mathbb{C}^{3}$ for every
$\mathbb{C}^{3}$ for every 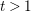 $t>1$ by means of a polynomial map. In addition, one of the immersions that we construct helps simplify the proof of the above CR-embeddability theorem and extend it to the larger parameter range
$t>1$ by means of a polynomial map. In addition, one of the immersions that we construct helps simplify the proof of the above CR-embeddability theorem and extend it to the larger parameter range 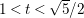 $1<t<\sqrt{5}/2$.
$1<t<\sqrt{5}/2$.
Alexander Isaev passed away in August 2019. Anticipating that he would not live to see the paper through final revision, he designated Nikolay Kruzhilin at Steklov Mathematical Institute, Moscow, as his proxy. The editorial board thanks Dr Kruzhilin for his kind assistance.