Research Article
A Study on Formal Deductions in the Primitive Logic
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-14
-
- Article
-
- You have access
- Export citation
Bayes Class and Wald Class
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 15-29
-
- Article
-
- You have access
- Export citation
Transitive Extensions of Certain Permutation Groups of Rank 3
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 31-36
-
- Article
-
- You have access
- Export citation
Existence of Non-Trivial Deformations of Some Inseparable Extension Fields
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 37-40
-
- Article
-
- You have access
- Export citation
Superharmonic Functions in a Domain of a Riemann Surface
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 41-55
-
- Article
-
- You have access
- Export citation
On Some Families of Analytic Functions on Riemann Surfaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 57-68
-
- Article
-
- You have access
- Export citation
A Remark on Peirce’s Rule in Many-Valued Logics
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 69-70
-
- Article
-
- You have access
- Export citation
On a Class of Truth-Value Evaluations of the Primitive Logic
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 71-80
-
- Article
-
- You have access
- Export citation
Higher Extensions of Abelian Varieties
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 81-88
-
- Article
-
- You have access
- Export citation
Positively Infinite Singularities of a Superharmonic Function
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 89-96
-
- Article
-
- You have access
- Export citation
Über einige Beispiele der Quasinormal—teiler einer p-Gruppe
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 97-103
-
- Article
-
- You have access
- Export citation
A Note on Simple Anti-Commutative Algebras Obtained from Reductive Homogeneous Spaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 105-124
-
- Article
-
- You have access
- Export citation
Certain Method for Generating a Series of Logics
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 125-129
-
- Article
-
- You have access
- Export citation
Equivalence Classes of Maximal Orders
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 131-171
-
- Article
-
- You have access
- Export citation
On Algebras of Dominant Dimension One
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 173-183
-
- Article
-
- You have access
- Export citation
Algebraic Deformations of Polarized Varieties
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 185-245
-
- Article
-
- You have access
- Export citation
A Note on Homotopy Invariance of Tangent Bundles
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 247-250
-
- Article
-
- You have access
- Export citation
On Osculating Systems of Differential Equations of Type (N, 1, 2)
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 251-278
-
- Article
-
- You have access
- Export citation
The Continuation of sections of Torsion-Free Coherent Analytic Sheaves
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 279-294
-
- Article
-
- You have access
- Export citation
Correction
Corrections to My Paper “Clifford Algebras and Families of Abelian Varieties”, Nagoya Math. J. 27 (1966), 435–446
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 295-296
-
- Article
-
- You have access
- Export citation

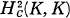 (see [2]) will be found in the image of
(see [2]) will be found in the image of 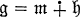 (subspace direct sum) with
(subspace direct sum) with 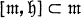 where
where 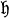 ) is the Lie algebra of
) is the Lie algebra of