Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T23:22:29.595Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of Non-Trivial Deformations of Some Inseparable Extension Fields

Published online by Cambridge University Press:  22 January 2016

Hiroshi Kimura
Hiroshi Kimura*
Affiliation:
Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A deformation theory for rings and algebras was introduced recently by M. Gerstenhaber [1]. Let K be an extension of a field k, and p denotes the characteristic. One of his results is that, if K is separable over k, then it is rigid. It was conjectured in [1] that, if K is not separable over k, then it is not rigid, and if it is further finitely generated, then an integrable element of 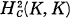(see [2]) will be found in the image of Sqp. In this note we shall study the above conjecture in certain special case.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 31 , January 1968 , pp. 37 - 40
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1968

References

[1] Gerstenhaber, M., On the deformation of rings and algebras, Ann. of Math. 79 (1964), 59–103.Google Scholar
[2] Harrison, D.K., Commutative algebras and cohomology, Trans. Amer. Math. Soc., 104 (1962), 191–204.Google Scholar
[3] Jacobson, N., Lecture in abstract algebra III, Van Nastrand, 1964.Google Scholar