We construct a stable formal model of a Lubin–Tate curve with level three, and study the action of a Weil group and a division algebra on its stable reduction. Further, we study a structure of cohomology of the Lubin–Tate curve. Our study is purely local and includes the case where the characteristic of the residue field of a local field is two.

This paper investigates the space of codimension zero embeddings of a Poincaré duality space in a disk. One of our main results exhibits a tower that interpolates from the space of Poincaré immersions to a certain space of “unlinked” Poincaré embeddings. The layers of this tower are described in terms of the coefficient spectra of the identity appearing in Goodwillie’s homotopy functor calculus. We also answer a question posed to us by Sylvain Cappell. The appendix proposes a conjectural relationship between our tower and the manifold calculus tower for the smooth embedding space.

In this paper, we investigate the mixed Hodge structures of the moduli space of $\boldsymbol{\unicode[STIX]{x1D6FC}}$ -stable parabolic Higgs bundles and the moduli space of $\boldsymbol{\unicode[STIX]{x1D6FC}}$ -stable regular singular parabolic connections. We show that the mixed Hodge polynomials are independent of the choice of generic eigenvalues and the mixed Hodge structures of these moduli spaces are pure. Moreover, by the Riemann–Hilbert correspondence, the Poincaré polynomials of character varieties are independent of the choice of generic eigenvalues.

In this paper we introduce and study Miyashita action in the context of monoidal categories aiming by this to provide a common framework of previous studies in the literature. We make a special emphasis of this action on Azumaya monoids. To this end, we develop the theory of invertible bimodules over different monoids (a sort of Morita contexts) in general monoidal categories as well as their corresponding Miyashita action. Roughly speaking, a Miyashita action is a homomorphism of groups from the group of all isomorphic classes of invertible subobjects of a given monoid to its group of automorphisms. In the symmetric case, we show that for certain Azumaya monoids, which are abundant in practice, the corresponding Miyashita action is always an isomorphism of groups. This generalizes Miyashita’s classical result and sheds light on other applications of geometric nature which cannot be treated using the classical theory. In order to illustrate our methods, we give a concrete application to the category of comodules over commutative (flat) Hopf algebroids. This obviously includes the special cases of split Hopf algebroids (action groupoids), which for instance cover the situation of the action of an affine algebraic group on an affine algebraic variety.

If 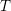$T$ and 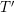$T^{\prime }$ are two cluster-tilting objects of an acyclic cluster category related by a mutation, their endomorphism algebras are nearly Morita equivalent (Buan et al., Cluster-tilted algebras, Trans. Amer. Math. Soc. 359(1) (2007), 323–332 (electronic)); that is, their module categories are equivalent “up to a simple module”. This result has been generalized by Yang, using a result of Plamondon, to any simple mutation of maximal rigid objects in a 2-Calabi–Yau triangulated category. In this paper, we investigate the more general case of any mutation of a (non-necessarily maximal) rigid object in a triangulated category with a Serre functor. In that setup, the endomorphism algebras might not be nearly Morita equivalent, and we obtain a weaker property that we call pseudo-Morita equivalence. Inspired by Buan and Marsh (From triangulated categories to module categories via localization II: calculus of fractions, J. Lond. Math. Soc. (2) 86(1) (2012), 152–170; From triangulated categories to module categories via localisation, Trans. Amer. Math. Soc. 365(6) (2013), 2845–2861), we also describe our result in terms of localizations.