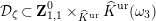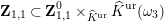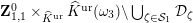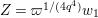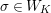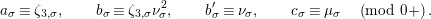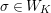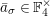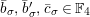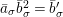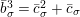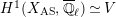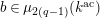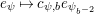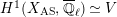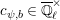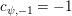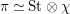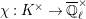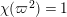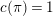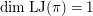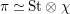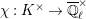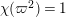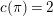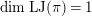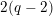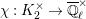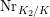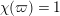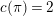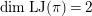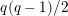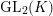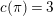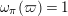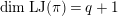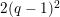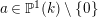Introduction
Let
![]() $K$
be a nonarchimedean local field with a finite residue field
$K$
be a nonarchimedean local field with a finite residue field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p$
. Let
$p$
. Let
![]() $\mathfrak{p}$
be the maximal ideal of the ring of integers
$\mathfrak{p}$
be the maximal ideal of the ring of integers
![]() ${\mathcal{O}}_{K}$
of
${\mathcal{O}}_{K}$
of
![]() $K$
. Let
$K$
. Let
![]() $n$
be a natural number. We write
$n$
be a natural number. We write
![]() $\text{LT}(\mathfrak{p}^{n})$
for the Lubin–Tate curve with full level
$\text{LT}(\mathfrak{p}^{n})$
for the Lubin–Tate curve with full level
![]() $n$
as a deformation space of formal
$n$
as a deformation space of formal
![]() ${\mathcal{O}}_{K}$
-modules by quasi-isogenies. Let
${\mathcal{O}}_{K}$
-modules by quasi-isogenies. Let
![]() $D$
be the central division algebra over
$D$
be the central division algebra over
![]() $K$
of invariant
$K$
of invariant
![]() $1/2$
. Let
$1/2$
. Let
![]() $\ell$
be a prime number different from
$\ell$
be a prime number different from
![]() $p$
. We write
$p$
. We write
![]() $\mathbf{C}$
for the completion of an algebraic closure of
$\mathbf{C}$
for the completion of an algebraic closure of
![]() $K$
. Then, the groups
$K$
. Then, the groups
![]() $W_{K}$
,
$W_{K}$
,
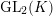 $\text{GL}_{2}(K)$
and
$\text{GL}_{2}(K)$
and
![]() $D^{\times }$
act on
$D^{\times }$
act on
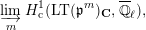 $$\begin{eqnarray}\varinjlim _{m}H_{\text{c}}^{1}(\text{LT}(\mathfrak{p}^{m})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell }),\end{eqnarray}$$
$$\begin{eqnarray}\varinjlim _{m}H_{\text{c}}^{1}(\text{LT}(\mathfrak{p}^{m})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell }),\end{eqnarray}$$
and these actions partially realize the local Langlands correspondence and the local Jacquet–Langlands correspondence for
![]() $\text{GL}_{2}$
. The realization of the local Langlands correspondence was proved by global automorphic methods in [Reference CarayolCa]. Since Lubin–Tate curves are purely local objects, it is desirable to have a purely local proof which only makes use of the geometry of Lubin–Tate curves.
$\text{GL}_{2}$
. The realization of the local Langlands correspondence was proved by global automorphic methods in [Reference CarayolCa]. Since Lubin–Tate curves are purely local objects, it is desirable to have a purely local proof which only makes use of the geometry of Lubin–Tate curves.
We put
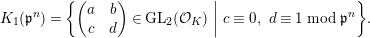 $$\begin{eqnarray}K_{1}(\mathfrak{p}^{n})=\biggl\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \text{GL}_{2}({\mathcal{O}}_{K})~\bigg|~c\equiv 0,~d\equiv 1\hspace{0.2em}\bmod \hspace{0.2em}\mathfrak{p}^{n}\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}K_{1}(\mathfrak{p}^{n})=\biggl\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \text{GL}_{2}({\mathcal{O}}_{K})~\bigg|~c\equiv 0,~d\equiv 1\hspace{0.2em}\bmod \hspace{0.2em}\mathfrak{p}^{n}\biggr\}.\end{eqnarray}$$
Let
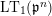 $\text{LT}_{1}(\mathfrak{p}^{n})$
be the Lubin–Tate curve with level
$\text{LT}_{1}(\mathfrak{p}^{n})$
be the Lubin–Tate curve with level
![]() $K_{1}(\mathfrak{p}^{n})$
as a deformation space of formal
$K_{1}(\mathfrak{p}^{n})$
as a deformation space of formal
![]() ${\mathcal{O}}_{K}$
-modules by quasi-isogenies. Then, the cohomology group
${\mathcal{O}}_{K}$
-modules by quasi-isogenies. Then, the cohomology group
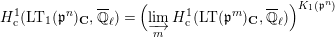 $$\begin{eqnarray}H_{\text{c}}^{1}(\text{LT}_{1}(\mathfrak{p}^{n})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell })=\Bigl(\varinjlim _{m}H_{\text{c}}^{1}(\text{LT}(\mathfrak{p}^{m})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell })\Bigr)^{K_{1}(\mathfrak{p}^{n})}\end{eqnarray}$$
$$\begin{eqnarray}H_{\text{c}}^{1}(\text{LT}_{1}(\mathfrak{p}^{n})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell })=\Bigl(\varinjlim _{m}H_{\text{c}}^{1}(\text{LT}(\mathfrak{p}^{m})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell })\Bigr)^{K_{1}(\mathfrak{p}^{n})}\end{eqnarray}$$
will give representations of
![]() $W_{K}$
and
$W_{K}$
and
![]() $D^{\times }$
that correspond to smooth irreducible representations of
$D^{\times }$
that correspond to smooth irreducible representations of
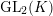 $\text{GL}_{2}(K)$
with conductor less than or equal to
$\text{GL}_{2}(K)$
with conductor less than or equal to
![]() $n$
. The purpose of this paper is to study this cohomology in the case
$n$
. The purpose of this paper is to study this cohomology in the case
![]() $n=3$
. We note that
$n=3$
. We note that
![]() $3$
is the smallest conductor of a two-dimensional representation of
$3$
is the smallest conductor of a two-dimensional representation of
![]() $W_{K}$
which cannot be written as an induction of a character. Such a representation is called a primitive representation.
$W_{K}$
which cannot be written as an induction of a character. Such a representation is called a primitive representation.
Our method is purely local and geometric. In fact, we construct a stable model of the connected Lubin–Tate curve
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
with level
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
with level
![]() $K_{1}(\mathfrak{p}^{3})$
by using the theory of semistable coverings (cf. [Reference Coleman and McMurdyCM, Section 2.3]). Our study includes the case where
$K_{1}(\mathfrak{p}^{3})$
by using the theory of semistable coverings (cf. [Reference Coleman and McMurdyCM, Section 2.3]). Our study includes the case where
![]() $p=2$
, and in this case, primitive Galois representations of conductor
$p=2$
, and in this case, primitive Galois representations of conductor
![]() $3$
appear in the cohomology of
$3$
appear in the cohomology of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
. It gives a geometric understanding of a realization of the primitive Galois representations.
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
. It gives a geometric understanding of a realization of the primitive Galois representations.
Our method of the calculation of the stable reduction is similar to that in [Reference Coleman and McMurdyCM]. In [Reference Coleman and McMurdyCM], Coleman and McMurdy calculate the stable reduction of the modular curve
![]() $X_{0}(p^{3})$
under the assumption
$X_{0}(p^{3})$
under the assumption
![]() $p\geqslant 13$
. The calculation of the stable reductions in the modular curve setting is equivalent to that in the Lubin–Tate setting where
$p\geqslant 13$
. The calculation of the stable reductions in the modular curve setting is equivalent to that in the Lubin–Tate setting where
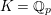 $K=\mathbb{Q}_{p}$
. As for the calculation of the stable reduction of the modular curve
$K=\mathbb{Q}_{p}$
. As for the calculation of the stable reduction of the modular curve
![]() $X_{1}(p^{n})$
, it is given in [Reference Deligne and RapoportDR] if
$X_{1}(p^{n})$
, it is given in [Reference Deligne and RapoportDR] if
![]() $n=1$
.
$n=1$
.
We explain the contents of this paper. In Section 1, we recall a definition of the connected Lubin–Tate curve, and study the action of a division algebra in a general setting. In Section 2, we study the cohomology of Lubin–Tate curves as representations of
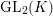 $\text{GL}_{2}(K)$
by purely local methods. By this result, we can calculate the genus of some Lubin–Tate curves. In Section 3, we construct a stable covering of the connected Lubin–Tate curve with level
$\text{GL}_{2}(K)$
by purely local methods. By this result, we can calculate the genus of some Lubin–Tate curves. In Section 3, we construct a stable covering of the connected Lubin–Tate curve with level
![]() $K_{1}(\mathfrak{p}^{2})$
, which is used to study a covering of
$K_{1}(\mathfrak{p}^{2})$
, which is used to study a covering of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
.
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
.
In Section 4, we define several affinoid subspaces
![]() $\mathbf{Y}_{1,2}$
,
$\mathbf{Y}_{1,2}$
,
![]() $\mathbf{Y}_{2,1}$
and
$\mathbf{Y}_{2,1}$
and
![]() $\mathbf{Z}_{1,1}^{0}$
of
$\mathbf{Z}_{1,1}^{0}$
of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
, and calculate their reductions. Let
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
, and calculate their reductions. Let
![]() $k^{\text{ac}}$
be the residue field of
$k^{\text{ac}}$
be the residue field of
![]() $\mathbf{C}$
. We put
$\mathbf{C}$
. We put
![]() $q=|k|$
and
$q=|k|$
and
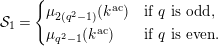 $$\begin{eqnarray}{\mathcal{S}}_{1}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})\quad & \text{if }q\text{ is odd},\\ \unicode[STIX]{x1D707}_{q^{2}-1}(k^{\text{ac}})\quad & \text{if }q\text{ is even}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{S}}_{1}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})\quad & \text{if }q\text{ is odd},\\ \unicode[STIX]{x1D707}_{q^{2}-1}(k^{\text{ac}})\quad & \text{if }q\text{ is even}.\end{array}\right.\end{eqnarray}$$
The reductions of
![]() $\mathbf{Y}_{1,2}$
and
$\mathbf{Y}_{1,2}$
and
![]() $\mathbf{Y}_{2,1}$
are isomorphic to the affine curve defined by
$\mathbf{Y}_{2,1}$
are isomorphic to the affine curve defined by
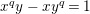 $x^{q}y-xy^{q}=1$
. This affine curve has genus
$x^{q}y-xy^{q}=1$
. This affine curve has genus
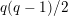 $q(q-1)/2$
, and is called the Deligne–Lusztig curve for
$q(q-1)/2$
, and is called the Deligne–Lusztig curve for
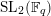 $\text{SL}_{2}(\mathbb{F}_{q})$
or the Drinfeld curve. Here, the genus of a curve means the genus of the smooth compactification of the normalization of the curve. The reduction
$\text{SL}_{2}(\mathbb{F}_{q})$
or the Drinfeld curve. Here, the genus of a curve means the genus of the smooth compactification of the normalization of the curve. The reduction
![]() $\overline{\mathbf{Z}}_{1,1}^{0}$
of
$\overline{\mathbf{Z}}_{1,1}^{0}$
of
![]() $\mathbf{Z}_{1,1}^{0}$
is isomorphic to the affine curve defined by
$\mathbf{Z}_{1,1}^{0}$
is isomorphic to the affine curve defined by
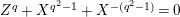 $Z^{q}+X^{q^{2}-1}+X^{-(q^{2}-1)}=0$
. This affine curve has genus
$Z^{q}+X^{q^{2}-1}+X^{-(q^{2}-1)}=0$
. This affine curve has genus
![]() $0$
and singularities at
$0$
and singularities at
![]() $X\in {\mathcal{S}}_{1}$
.
$X\in {\mathcal{S}}_{1}$
.
Next, we analyze tubular neighborhoods
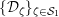 $\{{\mathcal{D}}_{\unicode[STIX]{x1D701}}\}_{\unicode[STIX]{x1D701}\in {\mathcal{S}}_{1}}$
of the singular points of
$\{{\mathcal{D}}_{\unicode[STIX]{x1D701}}\}_{\unicode[STIX]{x1D701}\in {\mathcal{S}}_{1}}$
of the singular points of
![]() $\overline{\mathbf{Z}}_{1,1}^{0}$
. If
$\overline{\mathbf{Z}}_{1,1}^{0}$
. If
![]() $q$
is odd,
$q$
is odd,
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
is a basic wide open space with the underlying affinoid
${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
is a basic wide open space with the underlying affinoid
![]() $\mathbf{X}_{\unicode[STIX]{x1D701}}$
. See [Reference Coleman and McMurdyCM, 2B] for the precise definition of a basic wide open space. Roughly speaking, it is a smooth geometrically connected one-dimensional rigid space which contains an affinoid such that the reduction of the affinoid is irreducible and has at worst ordinary double points as singularities, and the complement of the affinoid is a disjoint union of open annuli. The reduction of
$\mathbf{X}_{\unicode[STIX]{x1D701}}$
. See [Reference Coleman and McMurdyCM, 2B] for the precise definition of a basic wide open space. Roughly speaking, it is a smooth geometrically connected one-dimensional rigid space which contains an affinoid such that the reduction of the affinoid is irreducible and has at worst ordinary double points as singularities, and the complement of the affinoid is a disjoint union of open annuli. The reduction of
![]() $\mathbf{X}_{\unicode[STIX]{x1D701}}$
is isomorphic to the Artin–Schreier affine curve of degree
$\mathbf{X}_{\unicode[STIX]{x1D701}}$
is isomorphic to the Artin–Schreier affine curve of degree
![]() $2$
defined by
$2$
defined by
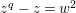 $z^{q}-z=w^{2}$
. This affine curve has genus
$z^{q}-z=w^{2}$
. This affine curve has genus
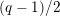 $(q-1)/2$
.
$(q-1)/2$
.
On the other hand, if
![]() $q$
is even, it is harder to analyze
$q$
is even, it is harder to analyze
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
, because the space
${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
, because the space
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
is not a basic wide open space. First, we find an affinoid
${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
is not a basic wide open space. First, we find an affinoid
![]() $\mathbf{P}_{\unicode[STIX]{x1D701}}^{0}$
. The reduction
$\mathbf{P}_{\unicode[STIX]{x1D701}}^{0}$
. The reduction
![]() $\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}^{0}$
of
$\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}^{0}$
of
![]() $\mathbf{P}_{\unicode[STIX]{x1D701}}^{0}$
has genus
$\mathbf{P}_{\unicode[STIX]{x1D701}}^{0}$
has genus
![]() $0$
and singular points parametrized by
$0$
and singular points parametrized by
![]() $\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
. Second, we analyze the tubular neighborhoods of singular points of
$\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
. Second, we analyze the tubular neighborhoods of singular points of
![]() $\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}^{0}$
. As a result, we find an affinoid
$\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}^{0}$
. As a result, we find an affinoid
![]() $\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
, whose reduction
$\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
, whose reduction
![]() $\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
is isomorphic to the affine curve defined by
$\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
is isomorphic to the affine curve defined by
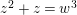 $z^{2}+z=w^{3}$
. The smooth compactification of this curve is the unique supersingular elliptic curve over
$z^{2}+z=w^{3}$
. The smooth compactification of this curve is the unique supersingular elliptic curve over
![]() $k^{\text{ac}}$
, whose
$k^{\text{ac}}$
, whose
![]() $j$
-invariant is
$j$
-invariant is
![]() $0$
, and its cohomology gives a primitive Galois representation. By using these affinoid spaces, we construct a covering
$0$
, and its cohomology gives a primitive Galois representation. By using these affinoid spaces, we construct a covering
![]() ${\mathcal{C}}_{1}(\mathfrak{p}^{3})$
of
${\mathcal{C}}_{1}(\mathfrak{p}^{3})$
of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
.
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
.
In Section 5, we calculate the action of
![]() ${\mathcal{O}}_{D}^{\times }$
on the reductions of the affinoid spaces in
${\mathcal{O}}_{D}^{\times }$
on the reductions of the affinoid spaces in
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
, where
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
, where
![]() ${\mathcal{O}}_{D}$
is the ring of integers of
${\mathcal{O}}_{D}$
is the ring of integers of
![]() $D$
. In Section 6, we calculate an action of a Weil group on the reductions. In the case where
$D$
. In Section 6, we calculate an action of a Weil group on the reductions. In the case where
![]() $q$
is even, we construct an
$q$
is even, we construct an
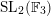 $\text{SL}_{2}(\mathbb{F}_{3})$
-Galois extension of
$\text{SL}_{2}(\mathbb{F}_{3})$
-Galois extension of
![]() $K^{\text{ur}}$
, and show that the Weil action on
$K^{\text{ur}}$
, and show that the Weil action on
![]() $\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
up to translations factors through the Weil group of the constructed extension. For such a Galois extension, see also [Reference WeilWeil, 31].
$\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
up to translations factors through the Weil group of the constructed extension. For such a Galois extension, see also [Reference WeilWeil, 31].
In Section 7, we show that the covering
![]() ${\mathcal{C}}_{1}(\mathfrak{p}^{3})$
is semistable. To show this, we calculate the summation of the genera of the reductions of the affinoid spaces in
${\mathcal{C}}_{1}(\mathfrak{p}^{3})$
is semistable. To show this, we calculate the summation of the genera of the reductions of the affinoid spaces in
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
, and compare it with the genus of
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
, and compare it with the genus of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
. Using the constructed semistable model, we study a structure of cohomology of
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
. Using the constructed semistable model, we study a structure of cohomology of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
.
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
.
The dual graph of the semistable reduction of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
in the case where
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
in the case where
![]() $q$
is even is the following:
$q$
is even is the following:
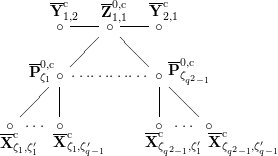
where
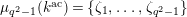 $\unicode[STIX]{x1D707}_{q^{2}-1}(k^{\text{ac}})=\{\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{q^{2}-1}\}$
,
$\unicode[STIX]{x1D707}_{q^{2}-1}(k^{\text{ac}})=\{\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{q^{2}-1}\}$
,
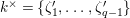 $k^{\times }=\{\unicode[STIX]{x1D701}_{1}^{\prime },\ldots ,\unicode[STIX]{x1D701}_{q-1}^{\prime }\}$
and
$k^{\times }=\{\unicode[STIX]{x1D701}_{1}^{\prime },\ldots ,\unicode[STIX]{x1D701}_{q-1}^{\prime }\}$
and
![]() $X^{\text{c}}$
denotes the smooth compactification of the normalization of
$X^{\text{c}}$
denotes the smooth compactification of the normalization of
![]() $X$
for a curve
$X$
for a curve
![]() $X$
over
$X$
over
![]() $k^{\text{ac}}$
. The constructed semistable model is in fact stable, except in the case where
$k^{\text{ac}}$
. The constructed semistable model is in fact stable, except in the case where
![]() $q=2$
. If
$q=2$
. If
![]() $q=2$
, we get the stable model by blowing down some
$q=2$
, we get the stable model by blowing down some
![]() $\mathbb{P}^{1}$
-components.
$\mathbb{P}^{1}$
-components.
The realization of the local Jacquet–Langlands correspondence in cohomology of Lubin–Tate curves was proved in [Reference MiedaMi] by a purely local method. Therefore, the remaining essential part of the study of the realization of the local Langlands correspondence is to study actions of Weil groups and division algebras. In the paper [Reference Imai and TsushimaIT3], we give a purely local proof of the realization of the local Langlands correspondence for representations of conductor three using the result of this paper.
Finally, we mention some recent progress on related topics according to a suggestion of a referee. In [Reference WeinsteinWein], Weinstein constructs semistable models of Lubin–Tate curves for arbitrary level in the case where the residue characteristic is not equal to two using Lubin–Tate perfectoid spaces. In [Reference Imai and TsushimaIT4] and [Reference Imai and TsushimaIT5], some of our results in this paper are generalized to arbitrary dimensional cases for Lubin–Tate perfectoid spaces. In [Reference Imai and TsushimaIT6], we construct an affinoid in the two-dimensional Lubin–Tate space such that the cohomology of the reduction of the affinoid realizes representations that are a bit more ramified than the epipelagic representations.
Notation
In this paper, we use the following notation. Let
![]() $K$
be a nonarchimedean local field. Let
$K$
be a nonarchimedean local field. Let
![]() ${\mathcal{O}}_{K}$
denote the ring of integers of
${\mathcal{O}}_{K}$
denote the ring of integers of
![]() $K$
, and let
$K$
, and let
![]() $k$
denote the residue field of
$k$
denote the residue field of
![]() $K$
. Let
$K$
. Let
![]() $p$
be the characteristic of
$p$
be the characteristic of
![]() $k$
. We fix a uniformizer
$k$
. We fix a uniformizer
![]() $\unicode[STIX]{x1D71B}$
of
$\unicode[STIX]{x1D71B}$
of
![]() $K$
. Let
$K$
. Let
![]() $q=|k|$
. We fix an algebraic closure
$q=|k|$
. We fix an algebraic closure
![]() $K^{\text{ac}}$
of
$K^{\text{ac}}$
of
![]() $K$
. For any finite extension
$K$
. For any finite extension
![]() $F$
of
$F$
of
![]() $K$
in
$K$
in
![]() $K^{\text{ac}}$
, let
$K^{\text{ac}}$
, let
![]() $G_{F}$
denote the absolute Galois group of
$G_{F}$
denote the absolute Galois group of
![]() $F$
, let
$F$
, let
![]() $W_{F}$
denote the Weil group of
$W_{F}$
denote the Weil group of
![]() $F$
, and let
$F$
, and let
![]() $I_{F}$
denote the inertia subgroup of
$I_{F}$
denote the inertia subgroup of
![]() $W_{F}$
. The completion of
$W_{F}$
. The completion of
![]() $K^{\text{ac}}$
is denoted by
$K^{\text{ac}}$
is denoted by
![]() $\mathbf{C}$
. Let
$\mathbf{C}$
. Let
![]() ${\mathcal{O}}_{\mathbf{C}}$
be the ring of integers of
${\mathcal{O}}_{\mathbf{C}}$
be the ring of integers of
![]() $\mathbf{C}$
, and let
$\mathbf{C}$
, and let
![]() $k^{\text{ac}}$
be the residue field of
$k^{\text{ac}}$
be the residue field of
![]() $\mathbf{C}$
. For an element
$\mathbf{C}$
. For an element
![]() $a\in {\mathcal{O}}_{\mathbf{C}}$
, we write
$a\in {\mathcal{O}}_{\mathbf{C}}$
, we write
![]() $\bar{a}$
for the image of
$\bar{a}$
for the image of
![]() $a$
by the reduction map
$a$
by the reduction map
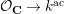 ${\mathcal{O}}_{\mathbf{C}}\rightarrow k^{\text{ac}}$
. Let
${\mathcal{O}}_{\mathbf{C}}\rightarrow k^{\text{ac}}$
. Let
![]() $v(\cdot )$
denote the valuation of
$v(\cdot )$
denote the valuation of
![]() $\mathbf{C}$
such that
$\mathbf{C}$
such that
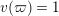 $v(\unicode[STIX]{x1D71B})=1$
. Let
$v(\unicode[STIX]{x1D71B})=1$
. Let
![]() $K^{\text{ur}}$
denote the maximal unramified extension of
$K^{\text{ur}}$
denote the maximal unramified extension of
![]() $K$
in
$K$
in
![]() $K^{\text{ac}}$
. The completion of
$K^{\text{ac}}$
. The completion of
![]() $K^{\text{ur}}$
is denoted by
$K^{\text{ur}}$
is denoted by
![]() $\widehat{K}^{\text{ur}}$
. For
$\widehat{K}^{\text{ur}}$
. For
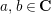 $a,b\in \mathbf{C}$
and a rational number
$a,b\in \mathbf{C}$
and a rational number
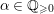 $\unicode[STIX]{x1D6FC}\in \mathbb{Q}_{{\geqslant}0}$
, we write
$\unicode[STIX]{x1D6FC}\in \mathbb{Q}_{{\geqslant}0}$
, we write
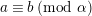 $a\equiv b\;(\text{mod}~\unicode[STIX]{x1D6FC})$
if we have
$a\equiv b\;(\text{mod}~\unicode[STIX]{x1D6FC})$
if we have
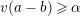 $v(a-b)\geqslant \unicode[STIX]{x1D6FC}$
, and
$v(a-b)\geqslant \unicode[STIX]{x1D6FC}$
, and
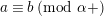 $a\equiv b\;(\text{mod}~\unicode[STIX]{x1D6FC}+)$
if we have
$a\equiv b\;(\text{mod}~\unicode[STIX]{x1D6FC}+)$
if we have
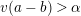 $v(a-b)>\unicode[STIX]{x1D6FC}$
. For a curve
$v(a-b)>\unicode[STIX]{x1D6FC}$
. For a curve
![]() $X$
over
$X$
over
![]() $k^{\text{ac}}$
, we denote by
$k^{\text{ac}}$
, we denote by
![]() $X^{c}$
the smooth compactification of the normalization of
$X^{c}$
the smooth compactification of the normalization of
![]() $X$
, and the genus of
$X$
, and the genus of
![]() $X$
means the genus of
$X$
means the genus of
![]() $X^{\text{c}}$
. For an affinoid
$X^{\text{c}}$
. For an affinoid
![]() $\mathbf{X}$
, we write
$\mathbf{X}$
, we write
![]() $\overline{\mathbf{X}}$
for its reduction. The category of sets is denoted by
$\overline{\mathbf{X}}$
for its reduction. The category of sets is denoted by
![]() $\mathbf{Set}$
. For a representation
$\mathbf{Set}$
. For a representation
![]() $\unicode[STIX]{x1D70F}$
of a group, the dual representation of
$\unicode[STIX]{x1D70F}$
of a group, the dual representation of
![]() $\unicode[STIX]{x1D70F}$
is denoted by
$\unicode[STIX]{x1D70F}$
is denoted by
![]() $\unicode[STIX]{x1D70F}^{\ast }$
. We take rational powers of
$\unicode[STIX]{x1D70F}^{\ast }$
. We take rational powers of
![]() $\unicode[STIX]{x1D71B}$
compatibly as needed.
$\unicode[STIX]{x1D71B}$
compatibly as needed.
1 Preliminaries
1.1 The universal deformation
Let
![]() $\unicode[STIX]{x1D6F4}$
denote a formal
$\unicode[STIX]{x1D6F4}$
denote a formal
![]() ${\mathcal{O}}_{K}$
-module of dimension
${\mathcal{O}}_{K}$
-module of dimension
![]() $1$
and height
$1$
and height
![]() $2$
over
$2$
over
![]() $k^{\text{ac}}$
, which is unique up to isomorphism. Let
$k^{\text{ac}}$
, which is unique up to isomorphism. Let
![]() $n$
be a natural number. We define
$n$
be a natural number. We define
![]() $K_{1}(\mathfrak{p}^{n})$
as in the introduction. In the following, we define the connected Lubin–Tate curve
$K_{1}(\mathfrak{p}^{n})$
as in the introduction. In the following, we define the connected Lubin–Tate curve
![]() $\mathbf{X}_{1}(\mathfrak{p}^{n})$
with level
$\mathbf{X}_{1}(\mathfrak{p}^{n})$
with level
![]() $K_{1}(\mathfrak{p}^{n})$
.
$K_{1}(\mathfrak{p}^{n})$
.
Let
![]() ${\mathcal{C}}$
be the category of Noetherian complete local
${\mathcal{C}}$
be the category of Noetherian complete local
![]() ${\mathcal{O}}_{\widehat{K}^{\text{ur}}}$
-algebras with residue field
${\mathcal{O}}_{\widehat{K}^{\text{ur}}}$
-algebras with residue field
![]() $k^{\text{ac}}$
. For
$k^{\text{ac}}$
. For
![]() $A\in {\mathcal{C}}$
, a formal
$A\in {\mathcal{C}}$
, a formal
![]() ${\mathcal{O}}_{K}$
-module
${\mathcal{O}}_{K}$
-module
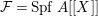 ${\mathcal{F}}=\text{Spf}\,A[[X]]$
over
${\mathcal{F}}=\text{Spf}\,A[[X]]$
over
![]() $A$
and an
$A$
and an
![]() $A$
-valued point
$A$
-valued point
![]() $P$
of
$P$
of
![]() ${\mathcal{F}}$
, the corresponding element of the maximal ideal of
${\mathcal{F}}$
, the corresponding element of the maximal ideal of
![]() $A$
is denoted by
$A$
is denoted by
![]() $x(P)$
. We consider the functor
$x(P)$
. We consider the functor
 $$\begin{eqnarray}{\mathcal{A}}_{1}(\mathfrak{p}^{n}):{\mathcal{C}}\rightarrow \mathbf{Set};\qquad A\mapsto [({\mathcal{F}},\unicode[STIX]{x1D704},P)],\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{1}(\mathfrak{p}^{n}):{\mathcal{C}}\rightarrow \mathbf{Set};\qquad A\mapsto [({\mathcal{F}},\unicode[STIX]{x1D704},P)],\end{eqnarray}$$
where
![]() ${\mathcal{F}}$
is a formal
${\mathcal{F}}$
is a formal
![]() ${\mathcal{O}}_{K}$
-module over
${\mathcal{O}}_{K}$
-module over
![]() $A$
with an isomorphism
$A$
with an isomorphism
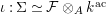 $\unicode[STIX]{x1D704}:\unicode[STIX]{x1D6F4}\simeq {\mathcal{F}}\otimes _{A}k^{\text{ac}}$
and
$\unicode[STIX]{x1D704}:\unicode[STIX]{x1D6F4}\simeq {\mathcal{F}}\otimes _{A}k^{\text{ac}}$
and
![]() $P$
is a
$P$
is a
![]() $\unicode[STIX]{x1D71B}^{n}$
-torsion point of
$\unicode[STIX]{x1D71B}^{n}$
-torsion point of
![]() ${\mathcal{F}}$
such that
${\mathcal{F}}$
such that
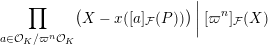 $$\begin{eqnarray}\mathop{\prod }_{a\in {\mathcal{O}}_{K}/\unicode[STIX]{x1D71B}^{n}{\mathcal{O}}_{K}}(X-x([a]_{{\mathcal{F}}}(P)))\biggm\vert[\unicode[STIX]{x1D71B}^{n}]_{{\mathcal{F}}}(X)\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{a\in {\mathcal{O}}_{K}/\unicode[STIX]{x1D71B}^{n}{\mathcal{O}}_{K}}(X-x([a]_{{\mathcal{F}}}(P)))\biggm\vert[\unicode[STIX]{x1D71B}^{n}]_{{\mathcal{F}}}(X)\end{eqnarray}$$
in
![]() $A[[X]]$
. This functor is represented by a regular local ring
$A[[X]]$
. This functor is represented by a regular local ring
![]() ${\mathcal{R}}_{1}(\mathfrak{p}^{n})$
by [Reference Drinfel’dDr, Section 4.B) Lemma]. We write
${\mathcal{R}}_{1}(\mathfrak{p}^{n})$
by [Reference Drinfel’dDr, Section 4.B) Lemma]. We write
![]() $\mathfrak{X}_{1}(\mathfrak{p}^{n})$
for
$\mathfrak{X}_{1}(\mathfrak{p}^{n})$
for
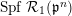 $\text{Spf}\,{\mathcal{R}}_{1}(\mathfrak{p}^{n})$
. Its generic fiber is denoted by
$\text{Spf}\,{\mathcal{R}}_{1}(\mathfrak{p}^{n})$
. Its generic fiber is denoted by
![]() $\mathbf{X}_{1}(\mathfrak{p}^{n})$
, which we call the connected Lubin–Tate curve with level
$\mathbf{X}_{1}(\mathfrak{p}^{n})$
, which we call the connected Lubin–Tate curve with level
![]() $K_{1}(\mathfrak{p}^{n})$
. The space
$K_{1}(\mathfrak{p}^{n})$
. The space
![]() $\mathbf{X}_{1}(\mathfrak{p}^{n})$
is a rigid analytic curve over
$\mathbf{X}_{1}(\mathfrak{p}^{n})$
is a rigid analytic curve over
![]() $\widehat{K}^{\text{ur}}$
. We can define the Lubin–Tate curve
$\widehat{K}^{\text{ur}}$
. We can define the Lubin–Tate curve
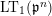 $\text{LT}_{1}(\mathfrak{p}^{n})$
with level
$\text{LT}_{1}(\mathfrak{p}^{n})$
with level
![]() $n$
by changing
$n$
by changing
![]() ${\mathcal{C}}$
to be the category of
${\mathcal{C}}$
to be the category of
![]() ${\mathcal{O}}_{\widehat{K}^{\text{ur}}}$
-algebras where
${\mathcal{O}}_{\widehat{K}^{\text{ur}}}$
-algebras where
![]() $\unicode[STIX]{x1D71B}$
is nilpotent, and
$\unicode[STIX]{x1D71B}$
is nilpotent, and
![]() $\unicode[STIX]{x1D704}$
to be a quasi-isogeny
$\unicode[STIX]{x1D704}$
to be a quasi-isogeny
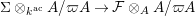 $\unicode[STIX]{x1D6F4}\otimes _{k^{\text{ac}}}A/\unicode[STIX]{x1D71B}A\rightarrow {\mathcal{F}}\otimes _{A}A/\unicode[STIX]{x1D71B}A$
. We consider
$\unicode[STIX]{x1D6F4}\otimes _{k^{\text{ac}}}A/\unicode[STIX]{x1D71B}A\rightarrow {\mathcal{F}}\otimes _{A}A/\unicode[STIX]{x1D71B}A$
. We consider
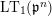 $\text{LT}_{1}(\mathfrak{p}^{n})$
as a rigid analytic curve over
$\text{LT}_{1}(\mathfrak{p}^{n})$
as a rigid analytic curve over
![]() $\widehat{K}^{\text{ur}}$
.
$\widehat{K}^{\text{ur}}$
.
The ring
![]() ${\mathcal{R}}_{1}(1)$
is isomorphic to the ring of formal power series
${\mathcal{R}}_{1}(1)$
is isomorphic to the ring of formal power series
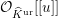 ${\mathcal{O}}_{\widehat{K}^{\text{ur}}}[[u]]$
. We simply write
${\mathcal{O}}_{\widehat{K}^{\text{ur}}}[[u]]$
. We simply write
![]() ${\mathcal{B}}(1)$
for
${\mathcal{B}}(1)$
for
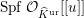 $\text{Spf}\,{\mathcal{O}}_{\widehat{K}^{\text{ur}}}[[u]]$
. Let
$\text{Spf}\,{\mathcal{O}}_{\widehat{K}^{\text{ur}}}[[u]]$
. Let
![]() $B(1)$
denote an open unit ball such that
$B(1)$
denote an open unit ball such that
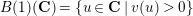 $B(1)(\mathbf{C})=\{u\in \mathbf{C}\mid v(u)>0\}$
. The generic fiber of
$B(1)(\mathbf{C})=\{u\in \mathbf{C}\mid v(u)>0\}$
. The generic fiber of
![]() ${\mathcal{B}}(1)$
is equal to
${\mathcal{B}}(1)$
is equal to
![]() $B(1)$
. Then, the space
$B(1)$
. Then, the space
![]() $\mathbf{X}_{1}(1)$
is identified with
$\mathbf{X}_{1}(1)$
is identified with
![]() $B(1)$
. Let
$B(1)$
. Let
![]() ${\mathcal{F}}^{\text{univ}}$
denote the universal formal
${\mathcal{F}}^{\text{univ}}$
denote the universal formal
![]() ${\mathcal{O}}_{K}$
-module over
${\mathcal{O}}_{K}$
-module over
![]() $\mathfrak{X}_{1}(1)$
.
$\mathfrak{X}_{1}(1)$
.
In this subsection, we choose a parametrization of
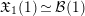 $\mathfrak{X}_{1}(1)\simeq {\mathcal{B}}(1)$
such that the universal formal
$\mathfrak{X}_{1}(1)\simeq {\mathcal{B}}(1)$
such that the universal formal
![]() ${\mathcal{O}}_{K}$
-module has a simple form. Let
${\mathcal{O}}_{K}$
-module has a simple form. Let
![]() ${\mathcal{F}}$
be a formal
${\mathcal{F}}$
be a formal
![]() ${\mathcal{O}}_{K}$
-module of dimension
${\mathcal{O}}_{K}$
-module of dimension
![]() $1$
over a flat
$1$
over a flat
![]() ${\mathcal{O}}_{K}$
-algebra
${\mathcal{O}}_{K}$
-algebra
![]() $R$
. For a nontrivial invariant differential
$R$
. For a nontrivial invariant differential
![]() $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
![]() ${\mathcal{F}}$
, a logarithm of
${\mathcal{F}}$
, a logarithm of
![]() ${\mathcal{F}}$
means a unique isomorphism
${\mathcal{F}}$
means a unique isomorphism
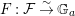 $F:{\mathcal{F}}\stackrel{{\sim}}{\rightarrow }\mathbb{G}_{a}$
over
$F:{\mathcal{F}}\stackrel{{\sim}}{\rightarrow }\mathbb{G}_{a}$
over
![]() $R\otimes K$
with
$R\otimes K$
with
![]() $dF=\unicode[STIX]{x1D714}$
(cf. [Reference Gross and HopkinsGH, 3]). In the following, we always take an invariant differential
$dF=\unicode[STIX]{x1D714}$
(cf. [Reference Gross and HopkinsGH, 3]). In the following, we always take an invariant differential
![]() $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
![]() ${\mathcal{F}}$
so that a logarithm
${\mathcal{F}}$
so that a logarithm
![]() $F$
has the following form:
$F$
has the following form:
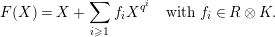 $$\begin{eqnarray}F(X)=X+\mathop{\sum }_{i\geqslant 1}f_{i}X^{q^{i}}\quad \text{with}~f_{i}\in R\otimes K.\end{eqnarray}$$
$$\begin{eqnarray}F(X)=X+\mathop{\sum }_{i\geqslant 1}f_{i}X^{q^{i}}\quad \text{with}~f_{i}\in R\otimes K.\end{eqnarray}$$
Let
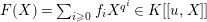 $F(X)=\sum _{i\geqslant 0}f_{i}X^{q^{i}}\in K[[u,X]]$
be the universal logarithm over
$F(X)=\sum _{i\geqslant 0}f_{i}X^{q^{i}}\in K[[u,X]]$
be the universal logarithm over
![]() ${\mathcal{O}}_{K}[[u]]$
. By [Reference Gross and HopkinsGH, (5.5), (12.3), Proposition 12.10], the coefficients
${\mathcal{O}}_{K}[[u]]$
. By [Reference Gross and HopkinsGH, (5.5), (12.3), Proposition 12.10], the coefficients
![]() $\{f_{i}\}_{i\geqslant 0}$
satisfy
$\{f_{i}\}_{i\geqslant 0}$
satisfy
![]() $f_{0}=1$
and
$f_{0}=1$
and
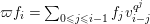 $\unicode[STIX]{x1D71B}f_{i}=\sum _{0\leqslant j\leqslant i-1}f_{j}v_{i-j}^{q^{j}}$
for
$\unicode[STIX]{x1D71B}f_{i}=\sum _{0\leqslant j\leqslant i-1}f_{j}v_{i-j}^{q^{j}}$
for
![]() $i\geqslant 1$
, where
$i\geqslant 1$
, where
![]() $v_{1}=u$
,
$v_{1}=u$
,
![]() $v_{2}=1$
and
$v_{2}=1$
and
![]() $v_{i}=0$
for
$v_{i}=0$
for
![]() $i\geqslant 3$
. Hence, we have the following:
$i\geqslant 3$
. Hence, we have the following:
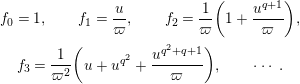 $$\begin{eqnarray}\begin{array}{@{}c@{}}f_{0}=1,\qquad f_{1}={\displaystyle \frac{u}{\unicode[STIX]{x1D71B}}},\qquad f_{2}={\displaystyle \frac{1}{\unicode[STIX]{x1D71B}}}\biggl(1+{\displaystyle \frac{u^{q+1}}{\unicode[STIX]{x1D71B}}}\biggr),\\ f_{3}={\displaystyle \frac{1}{\unicode[STIX]{x1D71B}^{2}}}\biggl(u+u^{q^{2}}+{\displaystyle \frac{u^{q^{2}+q+1}}{\unicode[STIX]{x1D71B}}}\biggr),\qquad \cdots \,.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}f_{0}=1,\qquad f_{1}={\displaystyle \frac{u}{\unicode[STIX]{x1D71B}}},\qquad f_{2}={\displaystyle \frac{1}{\unicode[STIX]{x1D71B}}}\biggl(1+{\displaystyle \frac{u^{q+1}}{\unicode[STIX]{x1D71B}}}\biggr),\\ f_{3}={\displaystyle \frac{1}{\unicode[STIX]{x1D71B}^{2}}}\biggl(u+u^{q^{2}}+{\displaystyle \frac{u^{q^{2}+q+1}}{\unicode[STIX]{x1D71B}}}\biggr),\qquad \cdots \,.\end{array}\end{eqnarray}$$
By [Reference Gross and HopkinsGH, Proposition 5.7] or [Reference HazewinkelHa, 21.5], if we set
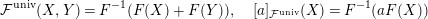 $$\begin{eqnarray}{\mathcal{F}}^{\text{univ}}(X,Y)=F^{-1}(F(X)+F(Y)),\quad [a]_{{\mathcal{F}}^{\text{univ}}}(X)=F^{-1}(aF(X))\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}^{\text{univ}}(X,Y)=F^{-1}(F(X)+F(Y)),\quad [a]_{{\mathcal{F}}^{\text{univ}}}(X)=F^{-1}(aF(X))\end{eqnarray}$$
for
![]() $a\in {\mathcal{O}}_{K}$
, it is known that these power series have coefficients in
$a\in {\mathcal{O}}_{K}$
, it is known that these power series have coefficients in
![]() ${\mathcal{O}}_{K}[[u]]$
and define the universal formal
${\mathcal{O}}_{K}[[u]]$
and define the universal formal
![]() ${\mathcal{O}}_{K}$
-module
${\mathcal{O}}_{K}$
-module
![]() ${\mathcal{F}}^{\text{univ}}$
over
${\mathcal{F}}^{\text{univ}}$
over
 ${\mathcal{O}}_{\widehat{K}^{\text{ur}}}[[u]]$
of dimension
${\mathcal{O}}_{\widehat{K}^{\text{ur}}}[[u]]$
of dimension
![]() $1$
and height
$1$
and height
![]() $2$
with logarithm
$2$
with logarithm
![]() $F(X)$
. We have the following approximation formula for
$F(X)$
. We have the following approximation formula for
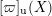 $[\unicode[STIX]{x1D71B}]_{\text{u}}(X)$
.
$[\unicode[STIX]{x1D71B}]_{\text{u}}(X)$
.
Lemma 1.1. We have the following congruence:
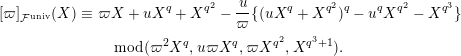 $$\begin{eqnarray}\displaystyle [\unicode[STIX]{x1D71B}]_{{\mathcal{F}}^{\text{univ}}}(X) & \equiv & \displaystyle \unicode[STIX]{x1D71B}X+uX^{q}+X^{q^{2}}-{\displaystyle \frac{u}{\unicode[STIX]{x1D71B}}}\{(uX^{q}+X^{q^{2}})^{q}-u^{q}X^{q^{2}}-X^{q^{3}}\}\nonumber\\ \displaystyle & & \displaystyle \quad \hspace{0.2em}\bmod \hspace{0.2em}(\unicode[STIX]{x1D71B}^{2}X^{q},u\unicode[STIX]{x1D71B}X^{q},\unicode[STIX]{x1D71B}X^{q^{2}},X^{q^{3}+1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [\unicode[STIX]{x1D71B}]_{{\mathcal{F}}^{\text{univ}}}(X) & \equiv & \displaystyle \unicode[STIX]{x1D71B}X+uX^{q}+X^{q^{2}}-{\displaystyle \frac{u}{\unicode[STIX]{x1D71B}}}\{(uX^{q}+X^{q^{2}})^{q}-u^{q}X^{q^{2}}-X^{q^{3}}\}\nonumber\\ \displaystyle & & \displaystyle \quad \hspace{0.2em}\bmod \hspace{0.2em}(\unicode[STIX]{x1D71B}^{2}X^{q},u\unicode[STIX]{x1D71B}X^{q},\unicode[STIX]{x1D71B}X^{q^{2}},X^{q^{3}+1}).\nonumber\end{eqnarray}$$
Proof. This follows from a direct computation using the relation
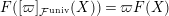 $F([\unicode[STIX]{x1D71B}]_{{\mathcal{F}}^{\text{univ}}}(X))=\unicode[STIX]{x1D71B}F(X)$
and (1.1).◻
$F([\unicode[STIX]{x1D71B}]_{{\mathcal{F}}^{\text{univ}}}(X))=\unicode[STIX]{x1D71B}F(X)$
and (1.1).◻
In the following,
![]() ${\mathcal{F}}^{\text{univ}}$
means the universal formal
${\mathcal{F}}^{\text{univ}}$
means the universal formal
![]() ${\mathcal{O}}_{K}$
-module with the identification
${\mathcal{O}}_{K}$
-module with the identification
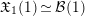 $\mathfrak{X}_{1}(1)\simeq {\mathcal{B}}(1)$
given by (1.2), and we simply write
$\mathfrak{X}_{1}(1)\simeq {\mathcal{B}}(1)$
given by (1.2), and we simply write
![]() $[a]_{\text{u}}$
for
$[a]_{\text{u}}$
for
![]() $[a]_{{\mathcal{F}}^{\text{univ}}}$
. The reduction of (1.2) gives a simple model of
$[a]_{{\mathcal{F}}^{\text{univ}}}$
. The reduction of (1.2) gives a simple model of
![]() $\unicode[STIX]{x1D6F4}$
such that
$\unicode[STIX]{x1D6F4}$
such that
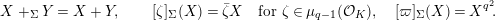 $$\begin{eqnarray}X+_{\unicode[STIX]{x1D6F4}}Y=X+Y,\qquad [\unicode[STIX]{x1D701}]_{\unicode[STIX]{x1D6F4}}(X)=\bar{\unicode[STIX]{x1D701}}X\quad \text{for }\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{q-1}({\mathcal{O}}_{K}),\quad [\unicode[STIX]{x1D71B}]_{\unicode[STIX]{x1D6F4}}(X)=X^{q^{2}}\!.\end{eqnarray}$$
$$\begin{eqnarray}X+_{\unicode[STIX]{x1D6F4}}Y=X+Y,\qquad [\unicode[STIX]{x1D701}]_{\unicode[STIX]{x1D6F4}}(X)=\bar{\unicode[STIX]{x1D701}}X\quad \text{for }\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{q-1}({\mathcal{O}}_{K}),\quad [\unicode[STIX]{x1D71B}]_{\unicode[STIX]{x1D6F4}}(X)=X^{q^{2}}\!.\end{eqnarray}$$
We put
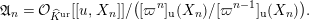 $$\begin{eqnarray}\mathfrak{A}_{n}={\mathcal{O}}_{\widehat{K}^{\text{ur}}}[[u,X_{n}]]/([\unicode[STIX]{x1D71B}^{n}]_{\text{u}}(X_{n})/[\unicode[STIX]{x1D71B}^{n-1}]_{\text{u}}(X_{n})).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{A}_{n}={\mathcal{O}}_{\widehat{K}^{\text{ur}}}[[u,X_{n}]]/([\unicode[STIX]{x1D71B}^{n}]_{\text{u}}(X_{n})/[\unicode[STIX]{x1D71B}^{n-1}]_{\text{u}}(X_{n})).\end{eqnarray}$$
Then, there is a natural identification
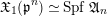 $$\begin{eqnarray}\mathfrak{X}_{1}(\mathfrak{p}^{n})\simeq \text{Spf}\,\mathfrak{A}_{n}\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{X}_{1}(\mathfrak{p}^{n})\simeq \text{Spf}\,\mathfrak{A}_{n}\end{eqnarray}$$
that is compatible with the identification
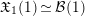 $\mathfrak{X}_{1}(1)\simeq {\mathcal{B}}(1)$
. The Lubin–Tate curve
$\mathfrak{X}_{1}(1)\simeq {\mathcal{B}}(1)$
. The Lubin–Tate curve
![]() $\mathbf{X}_{1}(\mathfrak{p}^{n})$
is identified with the generic fiber of the right-hand side of (1.4). We set
$\mathbf{X}_{1}(\mathfrak{p}^{n})$
is identified with the generic fiber of the right-hand side of (1.4). We set
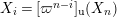 $X_{i}=[\unicode[STIX]{x1D71B}^{n-i}]_{\text{u}}(X_{n})$
for
$X_{i}=[\unicode[STIX]{x1D71B}^{n-i}]_{\text{u}}(X_{n})$
for
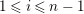 $1\leqslant i\leqslant n-1$
. We write
$1\leqslant i\leqslant n-1$
. We write
![]() $\mathfrak{X}(1)$
for
$\mathfrak{X}(1)$
for
![]() $\mathfrak{X}_{1}(1)$
.
$\mathfrak{X}_{1}(1)$
.
1.2 Action of a division algebra on
 $\mathfrak{X}_{1}(\mathfrak{p}^{n})$
$\mathfrak{X}_{1}(\mathfrak{p}^{n})$
Let
![]() $D$
be the central division algebra over
$D$
be the central division algebra over
![]() $K$
of invariant
$K$
of invariant
![]() $1/2$
. We write
$1/2$
. We write
![]() ${\mathcal{O}}_{D}$
for the ring of integers of
${\mathcal{O}}_{D}$
for the ring of integers of
![]() $D$
. In this subsection, we recall the left action of
$D$
. In this subsection, we recall the left action of
![]() ${\mathcal{O}}_{D}^{\times }$
on the space
${\mathcal{O}}_{D}^{\times }$
on the space
![]() $\mathfrak{X}_{1}(\mathfrak{p}^{n})$
.
$\mathfrak{X}_{1}(\mathfrak{p}^{n})$
.
Let
![]() $K_{2}$
be the unramified quadratic extension of
$K_{2}$
be the unramified quadratic extension of
![]() $K$
. Let
$K$
. Let
![]() $k_{2}$
be the residue field of
$k_{2}$
be the residue field of
![]() $K_{2}$
, and let
$K_{2}$
, and let
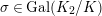 $\unicode[STIX]{x1D70E}\in \text{Gal}(K_{2}/K)$
be the nontrivial element. The ring
$\unicode[STIX]{x1D70E}\in \text{Gal}(K_{2}/K)$
be the nontrivial element. The ring
![]() ${\mathcal{O}}_{D}$
has the following description:
${\mathcal{O}}_{D}$
has the following description:
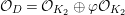 ${\mathcal{O}}_{D}={\mathcal{O}}_{K_{2}}\oplus \unicode[STIX]{x1D711}{\mathcal{O}}_{K_{2}}$
, with
${\mathcal{O}}_{D}={\mathcal{O}}_{K_{2}}\oplus \unicode[STIX]{x1D711}{\mathcal{O}}_{K_{2}}$
, with
![]() $\unicode[STIX]{x1D711}^{2}=\unicode[STIX]{x1D71B}$
and
$\unicode[STIX]{x1D711}^{2}=\unicode[STIX]{x1D71B}$
and
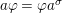 $a\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}a^{\unicode[STIX]{x1D70E}}$
for
$a\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}a^{\unicode[STIX]{x1D70E}}$
for
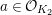 $a\in {\mathcal{O}}_{K_{2}}$
. We define an action of
$a\in {\mathcal{O}}_{K_{2}}$
. We define an action of
![]() ${\mathcal{O}}_{D}$
on
${\mathcal{O}}_{D}$
on
![]() $\unicode[STIX]{x1D6F4}$
by
$\unicode[STIX]{x1D6F4}$
by
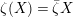 $\unicode[STIX]{x1D701}(X)=\bar{\unicode[STIX]{x1D701}}X$
for
$\unicode[STIX]{x1D701}(X)=\bar{\unicode[STIX]{x1D701}}X$
for
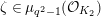 $\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{q^{2}-1}({\mathcal{O}}_{K_{2}})$
and
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{q^{2}-1}({\mathcal{O}}_{K_{2}})$
and
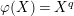 $\unicode[STIX]{x1D711}(X)=X^{q}$
. Then, this gives an isomorphism
$\unicode[STIX]{x1D711}(X)=X^{q}$
. Then, this gives an isomorphism
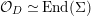 ${\mathcal{O}}_{D}\simeq \text{End}(\unicode[STIX]{x1D6F4})$
by [Reference Gross and HopkinsGH, Proposition 13.10].
${\mathcal{O}}_{D}\simeq \text{End}(\unicode[STIX]{x1D6F4})$
by [Reference Gross and HopkinsGH, Proposition 13.10].
Let
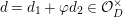 $d=d_{1}+\unicode[STIX]{x1D711}d_{2}\in {\mathcal{O}}_{D}^{\times }$
, where
$d=d_{1}+\unicode[STIX]{x1D711}d_{2}\in {\mathcal{O}}_{D}^{\times }$
, where
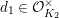 $d_{1}\in {\mathcal{O}}_{K_{2}}^{\times }$
and
$d_{1}\in {\mathcal{O}}_{K_{2}}^{\times }$
and
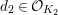 $d_{2}\in {\mathcal{O}}_{K_{2}}$
. By the definition of the action of
$d_{2}\in {\mathcal{O}}_{K_{2}}$
. By the definition of the action of
![]() ${\mathcal{O}}_{D}$
on
${\mathcal{O}}_{D}$
on
![]() $\unicode[STIX]{x1D6F4}$
, we have
$\unicode[STIX]{x1D6F4}$
, we have
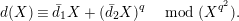 $$\begin{eqnarray}d(X)\equiv \bar{d}_{1}X+(\bar{d}_{2}X)^{q}\quad \hspace{0.2em}\bmod \hspace{0.2em}(X^{q^{2}}).\end{eqnarray}$$
$$\begin{eqnarray}d(X)\equiv \bar{d}_{1}X+(\bar{d}_{2}X)^{q}\quad \hspace{0.2em}\bmod \hspace{0.2em}(X^{q^{2}}).\end{eqnarray}$$
We take a lifting
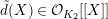 $\tilde{d}(X)\in {\mathcal{O}}_{K_{2}}[[X]]$
of
$\tilde{d}(X)\in {\mathcal{O}}_{K_{2}}[[X]]$
of
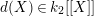 $d(X)\in k_{2}[[X]]$
. Let
$d(X)\in k_{2}[[X]]$
. Let
![]() ${\mathcal{F}}_{\tilde{d}}$
be the formal
${\mathcal{F}}_{\tilde{d}}$
be the formal
![]() ${\mathcal{O}}_{K}$
-module defined by
${\mathcal{O}}_{K}$
-module defined by
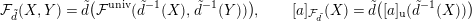 $$\begin{eqnarray}{\mathcal{F}}_{\tilde{d}}(X,Y)=\tilde{d}({\mathcal{F}}^{\text{univ}}(\tilde{d}^{-1}(X),\tilde{d}^{-1}(Y))),\qquad [a]_{{\mathcal{F}}_{\tilde{d}}}(X)=\tilde{d}([a]_{\text{u}}(\tilde{d}^{-1}(X)))\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}_{\tilde{d}}(X,Y)=\tilde{d}({\mathcal{F}}^{\text{univ}}(\tilde{d}^{-1}(X),\tilde{d}^{-1}(Y))),\qquad [a]_{{\mathcal{F}}_{\tilde{d}}}(X)=\tilde{d}([a]_{\text{u}}(\tilde{d}^{-1}(X)))\end{eqnarray}$$
for
![]() $a\in {\mathcal{O}}_{K}$
. Then, we have an isomorphism
$a\in {\mathcal{O}}_{K}$
. Then, we have an isomorphism
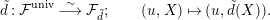 $$\begin{eqnarray}\tilde{d}:{\mathcal{F}}^{\text{univ}}\stackrel{{\sim}}{\longrightarrow }{\mathcal{F}}_{\tilde{d}};\qquad (u,X)\mapsto (u,\tilde{d}(X)).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{d}:{\mathcal{F}}^{\text{univ}}\stackrel{{\sim}}{\longrightarrow }{\mathcal{F}}_{\tilde{d}};\qquad (u,X)\mapsto (u,\tilde{d}(X)).\end{eqnarray}$$
By [Reference Gross and HopkinsGH, Proposition 14.7], the formal
![]() ${\mathcal{O}}_{K}$
-module
${\mathcal{O}}_{K}$
-module
![]() ${\mathcal{F}}_{\tilde{d}}$
with
${\mathcal{F}}_{\tilde{d}}$
with
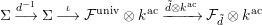 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}\stackrel{d^{-1}}{\longrightarrow }\unicode[STIX]{x1D6F4}\stackrel{\unicode[STIX]{x1D704}}{\longrightarrow }{\mathcal{F}}^{\text{univ}}\otimes k^{\text{ac}}\xrightarrow[]{\{}{\mathcal{F}}_{\tilde{d}}\otimes k^{\text{ac}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}\stackrel{d^{-1}}{\longrightarrow }\unicode[STIX]{x1D6F4}\stackrel{\unicode[STIX]{x1D704}}{\longrightarrow }{\mathcal{F}}^{\text{univ}}\otimes k^{\text{ac}}\xrightarrow[]{\{}{\mathcal{F}}_{\tilde{d}}\otimes k^{\text{ac}}\end{eqnarray}$$
gives an isomorphism
 $$\begin{eqnarray}d:\mathfrak{X}(1)\rightarrow \mathfrak{X}(1),\end{eqnarray}$$
$$\begin{eqnarray}d:\mathfrak{X}(1)\rightarrow \mathfrak{X}(1),\end{eqnarray}$$
which is independent of the choice of a lifting
![]() $\tilde{d}$
, such that there is the unique isomorphism
$\tilde{d}$
, such that there is the unique isomorphism
 $$\begin{eqnarray}j:d^{\ast }{\mathcal{F}}^{\text{univ}}\stackrel{{\sim}}{\longrightarrow }{\mathcal{F}}_{\tilde{d}};\qquad (u,X)\mapsto (u,j(X))\end{eqnarray}$$
$$\begin{eqnarray}j:d^{\ast }{\mathcal{F}}^{\text{univ}}\stackrel{{\sim}}{\longrightarrow }{\mathcal{F}}_{\tilde{d}};\qquad (u,X)\mapsto (u,j(X))\end{eqnarray}$$
satisfying
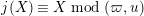 $j(X)\equiv X\hspace{0.2em}\bmod \hspace{0.2em}(\unicode[STIX]{x1D71B},u)$
, where
$j(X)\equiv X\hspace{0.2em}\bmod \hspace{0.2em}(\unicode[STIX]{x1D71B},u)$
, where
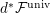 $d^{\ast }{\mathcal{F}}^{\text{univ}}$
denotes the pullback of
$d^{\ast }{\mathcal{F}}^{\text{univ}}$
denotes the pullback of
![]() ${\mathcal{F}}^{\text{univ}}$
over
${\mathcal{F}}^{\text{univ}}$
over
![]() $\mathfrak{X}(1)$
by the map (1.6). Hence, we have
$\mathfrak{X}(1)$
by the map (1.6). Hence, we have
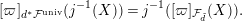 $$\begin{eqnarray}[\unicode[STIX]{x1D71B}]_{d^{\ast }{\mathcal{F}}^{\text{univ}}}(j^{-1}(X))=j^{-1}([\unicode[STIX]{x1D71B}]_{{\mathcal{F}}_{\tilde{d}}}(X)).\end{eqnarray}$$
$$\begin{eqnarray}[\unicode[STIX]{x1D71B}]_{d^{\ast }{\mathcal{F}}^{\text{univ}}}(j^{-1}(X))=j^{-1}([\unicode[STIX]{x1D71B}]_{{\mathcal{F}}_{\tilde{d}}}(X)).\end{eqnarray}$$
On the other hand, we have the following isomorphism:
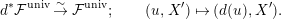 $$\begin{eqnarray}d^{\ast }{\mathcal{F}}^{\text{univ}}\stackrel{{\sim}}{\rightarrow }{\mathcal{F}}^{\text{univ}};\qquad (u,X^{\prime })\mapsto (d(u),X^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}d^{\ast }{\mathcal{F}}^{\text{univ}}\stackrel{{\sim}}{\rightarrow }{\mathcal{F}}^{\text{univ}};\qquad (u,X^{\prime })\mapsto (d(u),X^{\prime }).\end{eqnarray}$$
Furthermore, we consider the following isomorphism under the identification (1.4):
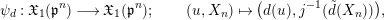 $$\begin{eqnarray}\unicode[STIX]{x1D713}_{d}:\mathfrak{X}_{1}(\mathfrak{p}^{n})\longrightarrow \mathfrak{X}_{1}(\mathfrak{p}^{n});\qquad (u,X_{n})\mapsto (d(u),j^{-1}(\tilde{d}(X_{n}))),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}_{d}:\mathfrak{X}_{1}(\mathfrak{p}^{n})\longrightarrow \mathfrak{X}_{1}(\mathfrak{p}^{n});\qquad (u,X_{n})\mapsto (d(u),j^{-1}(\tilde{d}(X_{n}))),\end{eqnarray}$$
which depends only on
![]() $d$
as in [Reference Gross and HopkinsGH, Proposition 14.7]. We put
$d$
as in [Reference Gross and HopkinsGH, Proposition 14.7]. We put
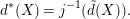 $$\begin{eqnarray}d^{\ast }(X)=j^{-1}(\tilde{d}(X)).\end{eqnarray}$$
$$\begin{eqnarray}d^{\ast }(X)=j^{-1}(\tilde{d}(X)).\end{eqnarray}$$
We define a left action of
![]() $d$
on
$d$
on
![]() $\mathfrak{X}_{1}(\mathfrak{p}^{n})$
by
$\mathfrak{X}_{1}(\mathfrak{p}^{n})$
by
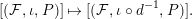 $$\begin{eqnarray}[({\mathcal{F}},\unicode[STIX]{x1D704},P)]\mapsto [({\mathcal{F}},\unicode[STIX]{x1D704}\circ d^{-1},P)].\end{eqnarray}$$
$$\begin{eqnarray}[({\mathcal{F}},\unicode[STIX]{x1D704},P)]\mapsto [({\mathcal{F}},\unicode[STIX]{x1D704}\circ d^{-1},P)].\end{eqnarray}$$
Then, this action coincides with
![]() $\unicode[STIX]{x1D713}_{d}$
by the definition.
$\unicode[STIX]{x1D713}_{d}$
by the definition.
By (1.5), we have
 $$\begin{eqnarray}\tilde{d}^{-1}(X)=d_{1}^{-1}X-d_{1}^{-(q+1)}d_{2}^{q}X^{q}\quad \hspace{0.2em}\bmod \hspace{0.2em}(\unicode[STIX]{x1D71B},X^{q^{2}})\end{eqnarray}$$
$$\begin{eqnarray}\tilde{d}^{-1}(X)=d_{1}^{-1}X-d_{1}^{-(q+1)}d_{2}^{q}X^{q}\quad \hspace{0.2em}\bmod \hspace{0.2em}(\unicode[STIX]{x1D71B},X^{q^{2}})\end{eqnarray}$$
in
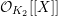 ${\mathcal{O}}_{K_{2}}[[X]]$
. We use the following lemma later to compute the
${\mathcal{O}}_{K_{2}}[[X]]$
. We use the following lemma later to compute the
![]() ${\mathcal{O}}_{D}^{\times }$
-action on the stable reduction of
${\mathcal{O}}_{D}^{\times }$
-action on the stable reduction of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
.
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
.
Lemma 1.2. We assume
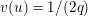 $v(u)=1/(2q)$
. Let
$v(u)=1/(2q)$
. Let
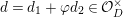 $d=d_{1}+\unicode[STIX]{x1D711}d_{2}\in {\mathcal{O}}_{D}^{\times }$
. We set
$d=d_{1}+\unicode[STIX]{x1D711}d_{2}\in {\mathcal{O}}_{D}^{\times }$
. We set
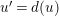 $u^{\prime }=d(u)$
. We change variables as
$u^{\prime }=d(u)$
. We change variables as
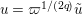 $u=\unicode[STIX]{x1D71B}^{1/(2q)}\tilde{u}$
and
$u=\unicode[STIX]{x1D71B}^{1/(2q)}\tilde{u}$
and
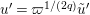 $u^{\prime }=\unicode[STIX]{x1D71B}^{1/(2q)}\tilde{u} ^{\prime }$
. Then, we have the following:
$u^{\prime }=\unicode[STIX]{x1D71B}^{1/(2q)}\tilde{u} ^{\prime }$
. Then, we have the following:
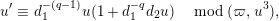 $$\begin{eqnarray}\displaystyle u^{\prime } & \equiv & \displaystyle d_{1}^{-(q-1)}u(1+d_{1}^{-q}d_{2}u)\quad \hspace{0.2em}\bmod \hspace{0.2em}(\unicode[STIX]{x1D71B},u^{3}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u^{\prime } & \equiv & \displaystyle d_{1}^{-(q-1)}u(1+d_{1}^{-q}d_{2}u)\quad \hspace{0.2em}\bmod \hspace{0.2em}(\unicode[STIX]{x1D71B},u^{3}),\end{eqnarray}$$
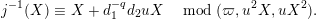 $$\begin{eqnarray}\displaystyle j^{-1}(X) & \equiv & \displaystyle X+d_{1}^{-q}d_{2}uX\quad \hspace{0.2em}\bmod \hspace{0.2em}(\unicode[STIX]{x1D71B},u^{2}X,uX^{2}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle j^{-1}(X) & \equiv & \displaystyle X+d_{1}^{-q}d_{2}uX\quad \hspace{0.2em}\bmod \hspace{0.2em}(\unicode[STIX]{x1D71B},u^{2}X,uX^{2}).\end{eqnarray}$$
Proof. We set
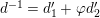 $d^{-1}=d_{1}^{\prime }+\unicode[STIX]{x1D711}d_{2}^{\prime }$
. Then,
$d^{-1}=d_{1}^{\prime }+\unicode[STIX]{x1D711}d_{2}^{\prime }$
. Then,
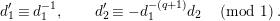 $$\begin{eqnarray}d_{1}^{\prime }\equiv d_{1}^{-1},\qquad d_{2}^{\prime }\equiv -d_{1}^{-(q+1)}d_{2}\quad \left(\text{mod}~1\right).\end{eqnarray}$$
$$\begin{eqnarray}d_{1}^{\prime }\equiv d_{1}^{-1},\qquad d_{2}^{\prime }\equiv -d_{1}^{-(q+1)}d_{2}\quad \left(\text{mod}~1\right).\end{eqnarray}$$
First, we prove (1.10). If
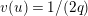 $v(u)=1/(2q)$
, the function
$v(u)=1/(2q)$
, the function
![]() $w(u)$
in [Reference Gross and HopkinsGH, (25.11)] is well approximated by a function
$w(u)$
in [Reference Gross and HopkinsGH, (25.11)] is well approximated by a function
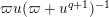 $\unicode[STIX]{x1D71B}u(\unicode[STIX]{x1D71B}+u^{q+1})^{-1}$
. By [Reference Gross and HopkinsGH, (25.13)], we have
$\unicode[STIX]{x1D71B}u(\unicode[STIX]{x1D71B}+u^{q+1})^{-1}$
. By [Reference Gross and HopkinsGH, (25.13)], we have
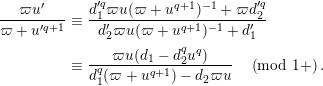 $$\begin{eqnarray}\displaystyle {\displaystyle \frac{\unicode[STIX]{x1D71B}u^{\prime }}{\unicode[STIX]{x1D71B}+u^{\prime q+1}}} & \equiv & \displaystyle {\displaystyle \frac{d_{1}^{\prime q}\unicode[STIX]{x1D71B}u(\unicode[STIX]{x1D71B}+u^{q+1})^{-1}+\unicode[STIX]{x1D71B}d_{2}^{\prime q}}{d_{2}^{\prime }\unicode[STIX]{x1D71B}u(\unicode[STIX]{x1D71B}+u^{q+1})^{-1}+d_{1}^{\prime }}}\nonumber\\ \displaystyle & \equiv & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D71B}u(d_{1}-d_{2}^{q}u^{q})}{d_{1}^{q}(\unicode[STIX]{x1D71B}+u^{q+1})-d_{2}\unicode[STIX]{x1D71B}u}}\quad \left(\text{mod}~1+\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{\unicode[STIX]{x1D71B}u^{\prime }}{\unicode[STIX]{x1D71B}+u^{\prime q+1}}} & \equiv & \displaystyle {\displaystyle \frac{d_{1}^{\prime q}\unicode[STIX]{x1D71B}u(\unicode[STIX]{x1D71B}+u^{q+1})^{-1}+\unicode[STIX]{x1D71B}d_{2}^{\prime q}}{d_{2}^{\prime }\unicode[STIX]{x1D71B}u(\unicode[STIX]{x1D71B}+u^{q+1})^{-1}+d_{1}^{\prime }}}\nonumber\\ \displaystyle & \equiv & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D71B}u(d_{1}-d_{2}^{q}u^{q})}{d_{1}^{q}(\unicode[STIX]{x1D71B}+u^{q+1})-d_{2}\unicode[STIX]{x1D71B}u}}\quad \left(\text{mod}~1+\right).\nonumber\end{eqnarray}$$
Hence, we acquire the following by
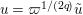 $u=\unicode[STIX]{x1D71B}^{1/(2q)}\tilde{u}$
and
$u=\unicode[STIX]{x1D71B}^{1/(2q)}\tilde{u}$
and
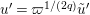 $u^{\prime }=\unicode[STIX]{x1D71B}^{1/(2q)}\tilde{u} ^{\prime }$
:
$u^{\prime }=\unicode[STIX]{x1D71B}^{1/(2q)}\tilde{u} ^{\prime }$
:
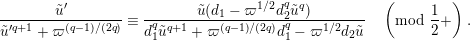 $$\begin{eqnarray}\displaystyle {\displaystyle \frac{\tilde{u} ^{\prime }}{\tilde{u} ^{\prime q+1}+\unicode[STIX]{x1D71B}^{(q-1)/(2q)}}}\equiv {\displaystyle \frac{\tilde{u} (d_{1}-\unicode[STIX]{x1D71B}^{1/2}d_{2}^{q}\tilde{u} ^{q})}{d_{1}^{q}\tilde{u} ^{q+1}+\unicode[STIX]{x1D71B}^{(q-1)/(2q)}d_{1}^{q}-\unicode[STIX]{x1D71B}^{1/2}d_{2}\tilde{u} }}\quad \left(\text{mod}~{\displaystyle \frac{1}{2}}+\right). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{\tilde{u} ^{\prime }}{\tilde{u} ^{\prime q+1}+\unicode[STIX]{x1D71B}^{(q-1)/(2q)}}}\equiv {\displaystyle \frac{\tilde{u} (d_{1}-\unicode[STIX]{x1D71B}^{1/2}d_{2}^{q}\tilde{u} ^{q})}{d_{1}^{q}\tilde{u} ^{q+1}+\unicode[STIX]{x1D71B}^{(q-1)/(2q)}d_{1}^{q}-\unicode[STIX]{x1D71B}^{1/2}d_{2}\tilde{u} }}\quad \left(\text{mod}~{\displaystyle \frac{1}{2}}+\right). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
By taking an inverse of the congruence (1.12), we obtain
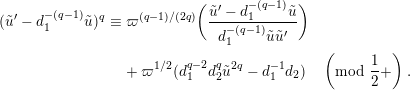 $$\begin{eqnarray}\displaystyle (\tilde{u} ^{\prime }-d_{1}^{-(q-1)}\tilde{u} )^{q} & \equiv & \displaystyle \unicode[STIX]{x1D71B}^{(q-1)/(2q)}\biggl({\displaystyle \frac{\tilde{u} ^{\prime }-d_{1}^{-(q-1)}\tilde{u} }{d_{1}^{-(q-1)}\tilde{u} \tilde{u} ^{\prime }}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D71B}^{1/2}(d_{1}^{q-2}d_{2}^{q}\tilde{u} ^{2q}-d_{1}^{-1}d_{2})\quad \left(\text{mod}~{\displaystyle \frac{1}{2}}+\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\tilde{u} ^{\prime }-d_{1}^{-(q-1)}\tilde{u} )^{q} & \equiv & \displaystyle \unicode[STIX]{x1D71B}^{(q-1)/(2q)}\biggl({\displaystyle \frac{\tilde{u} ^{\prime }-d_{1}^{-(q-1)}\tilde{u} }{d_{1}^{-(q-1)}\tilde{u} \tilde{u} ^{\prime }}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D71B}^{1/2}(d_{1}^{q-2}d_{2}^{q}\tilde{u} ^{2q}-d_{1}^{-1}d_{2})\quad \left(\text{mod}~{\displaystyle \frac{1}{2}}+\right).\end{eqnarray}$$
Now, we set
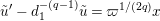 $\tilde{u} ^{\prime }-d_{1}^{-(q-1)}\tilde{u} =\unicode[STIX]{x1D71B}^{1/(2q)}x$
. By substituting this into (1.13) and dividing it by
$\tilde{u} ^{\prime }-d_{1}^{-(q-1)}\tilde{u} =\unicode[STIX]{x1D71B}^{1/(2q)}x$
. By substituting this into (1.13) and dividing it by
![]() $\unicode[STIX]{x1D71B}^{1/2}$
, we obtain
$\unicode[STIX]{x1D71B}^{1/2}$
, we obtain
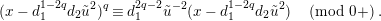 $$\begin{eqnarray}(x-d_{1}^{1-2q}d_{2}\tilde{u} ^{2})^{q}\equiv d_{1}^{2q-2}\tilde{u} ^{-2}(x-d_{1}^{1-2q}d_{2}\tilde{u} ^{2})\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
$$\begin{eqnarray}(x-d_{1}^{1-2q}d_{2}\tilde{u} ^{2})^{q}\equiv d_{1}^{2q-2}\tilde{u} ^{-2}(x-d_{1}^{1-2q}d_{2}\tilde{u} ^{2})\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
Since
![]() $x$
is an analytic function of
$x$
is an analytic function of
![]() $\tilde{u}$
, a congruence
$\tilde{u}$
, a congruence
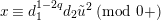 $x\equiv d_{1}^{1-2q}d_{2}\tilde{u} ^{2}\;(\text{mod}~0+)$
must hold. Hence, we have
$x\equiv d_{1}^{1-2q}d_{2}\tilde{u} ^{2}\;(\text{mod}~0+)$
must hold. Hence, we have
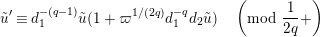 $$\begin{eqnarray}\tilde{u} ^{\prime }\equiv d_{1}^{-(q-1)}\tilde{u} (1+\unicode[STIX]{x1D71B}^{1/(2q)}d_{1}^{-q}d_{2}\tilde{u} )\quad \left(\text{mod}~{\displaystyle \frac{1}{2q}}+\right)\end{eqnarray}$$
$$\begin{eqnarray}\tilde{u} ^{\prime }\equiv d_{1}^{-(q-1)}\tilde{u} (1+\unicode[STIX]{x1D71B}^{1/(2q)}d_{1}^{-q}d_{2}\tilde{u} )\quad \left(\text{mod}~{\displaystyle \frac{1}{2q}}+\right)\end{eqnarray}$$
using
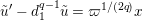 $\tilde{u} ^{\prime }-d_{1}^{q-1}\tilde{u} =\unicode[STIX]{x1D71B}^{1/(2q)}x$
. This implies (1.10), because
$\tilde{u} ^{\prime }-d_{1}^{q-1}\tilde{u} =\unicode[STIX]{x1D71B}^{1/(2q)}x$
. This implies (1.10), because
![]() $u^{\prime }$
is an analytic function of
$u^{\prime }$
is an analytic function of
![]() $u$
.
$u$
.
By Lemma 1.1, (1.7) and (1.9), we have
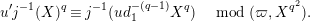 $$\begin{eqnarray}u^{\prime }j^{-1}(X)^{q}\equiv j^{-1}(ud_{1}^{-(q-1)}X^{q})\quad \hspace{0.2em}\bmod \hspace{0.2em}(\unicode[STIX]{x1D71B},X^{q^{2}}).\end{eqnarray}$$
$$\begin{eqnarray}u^{\prime }j^{-1}(X)^{q}\equiv j^{-1}(ud_{1}^{-(q-1)}X^{q})\quad \hspace{0.2em}\bmod \hspace{0.2em}(\unicode[STIX]{x1D71B},X^{q^{2}}).\end{eqnarray}$$
Hence, the assertion (1.11) follows from (1.10) and
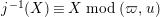 $j^{-1}(X)\equiv X\hspace{0.2em}\bmod \hspace{0.2em}(\unicode[STIX]{x1D71B},u)$
.◻
$j^{-1}(X)\equiv X\hspace{0.2em}\bmod \hspace{0.2em}(\unicode[STIX]{x1D71B},u)$
.◻
2 Cohomology of Lubin–Tate curve
Let
![]() $\ell$
be a prime number different from
$\ell$
be a prime number different from
![]() $p$
. We take an algebraic closure
$p$
. We take an algebraic closure
![]() $\overline{\mathbb{Q}}_{\ell }$
of
$\overline{\mathbb{Q}}_{\ell }$
of
![]() $\mathbb{Q}_{\ell }$
. Let
$\mathbb{Q}_{\ell }$
. Let
![]() $\text{LT}(\mathfrak{p}^{n})$
be the Lubin–Tate curve with full level
$\text{LT}(\mathfrak{p}^{n})$
be the Lubin–Tate curve with full level
![]() $n$
over
$n$
over
![]() $\widehat{K}^{\text{ur}}$
(cf. [Reference DatDa, 3.2]). We put
$\widehat{K}^{\text{ur}}$
(cf. [Reference DatDa, 3.2]). We put
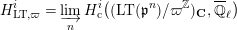 $$\begin{eqnarray}H_{\text{LT},\unicode[STIX]{x1D71B}}^{i}=\varinjlim _{n}H_{\text{c}}^{i}((\text{LT}(\mathfrak{p}^{n})/\unicode[STIX]{x1D71B}^{\mathbb{Z}})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell })\end{eqnarray}$$
$$\begin{eqnarray}H_{\text{LT},\unicode[STIX]{x1D71B}}^{i}=\varinjlim _{n}H_{\text{c}}^{i}((\text{LT}(\mathfrak{p}^{n})/\unicode[STIX]{x1D71B}^{\mathbb{Z}})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell })\end{eqnarray}$$
for any nonnegative integer
![]() $i$
, where
$i$
, where
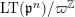 $\text{LT}(\mathfrak{p}^{n})/\unicode[STIX]{x1D71B}^{\mathbb{Z}}$
denotes the quotient of
$\text{LT}(\mathfrak{p}^{n})/\unicode[STIX]{x1D71B}^{\mathbb{Z}}$
denotes the quotient of
![]() $\text{LT}(\mathfrak{p}^{n})$
by the action of
$\text{LT}(\mathfrak{p}^{n})$
by the action of
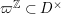 $\unicode[STIX]{x1D71B}^{\mathbb{Z}}\subset D^{\times }$
. Then, we can define an action of
$\unicode[STIX]{x1D71B}^{\mathbb{Z}}\subset D^{\times }$
. Then, we can define an action of
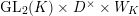 $\text{GL}_{2}(K)\times D^{\times }\times W_{K}$
on
$\text{GL}_{2}(K)\times D^{\times }\times W_{K}$
on
![]() $H_{\text{LT},\unicode[STIX]{x1D71B}}^{i}$
for a nonnegative integer
$H_{\text{LT},\unicode[STIX]{x1D71B}}^{i}$
for a nonnegative integer
![]() $i$
(cf. [Reference DatDa, 3.2, 3.3]).
$i$
(cf. [Reference DatDa, 3.2, 3.3]).
We write
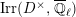 $\text{Irr}(D^{\times },\overline{\mathbb{Q}}_{\ell })$
for the set of isomorphism classes of irreducible smooth representations of
$\text{Irr}(D^{\times },\overline{\mathbb{Q}}_{\ell })$
for the set of isomorphism classes of irreducible smooth representations of
![]() $D^{\times }$
over
$D^{\times }$
over
![]() $\overline{\mathbb{Q}}_{\ell }$
, and
$\overline{\mathbb{Q}}_{\ell }$
, and
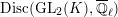 $\text{Disc}(\text{GL}_{2}(K),\overline{\mathbb{Q}}_{\ell })$
for the set of isomorphism classes of irreducible discrete series representations of
$\text{Disc}(\text{GL}_{2}(K),\overline{\mathbb{Q}}_{\ell })$
for the set of isomorphism classes of irreducible discrete series representations of
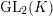 $\text{GL}_{2}(K)$
over
$\text{GL}_{2}(K)$
over
![]() $\overline{\mathbb{Q}}_{\ell }$
. Let
$\overline{\mathbb{Q}}_{\ell }$
. Let
 $$\begin{eqnarray}\text{JL}:\text{Irr}(D^{\times },\overline{\mathbb{Q}}_{\ell })\rightarrow \text{Disc}(\text{GL}_{2}(K),\overline{\mathbb{Q}}_{\ell })\end{eqnarray}$$
$$\begin{eqnarray}\text{JL}:\text{Irr}(D^{\times },\overline{\mathbb{Q}}_{\ell })\rightarrow \text{Disc}(\text{GL}_{2}(K),\overline{\mathbb{Q}}_{\ell })\end{eqnarray}$$
be the local Jacquet–Langlands correspondence. We denote by
![]() $\text{LJ}$
the inverse of
$\text{LJ}$
the inverse of
![]() $\text{JL}$
. For an irreducible smooth representation
$\text{JL}$
. For an irreducible smooth representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
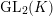 $\text{GL}_{2}(K)$
, let
$\text{GL}_{2}(K)$
, let
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$
denote the central character of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$
denote the central character of
![]() $\unicode[STIX]{x1D70B}$
. We write
$\unicode[STIX]{x1D70B}$
. We write
![]() $\text{St}$
for the Steinberg representation of
$\text{St}$
for the Steinberg representation of
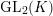 $\text{GL}_{2}(K)$
.
$\text{GL}_{2}(K)$
.
The following fact is well known as a corollary of the Deligne–Carayol conjecture. Here, we give a purely local proof of this fact.
Proposition 2.1. We have isomorphisms
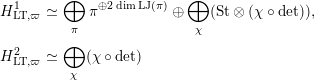 $$\begin{eqnarray}\displaystyle H_{\text{LT},\unicode[STIX]{x1D71B}}^{1} & \simeq & \displaystyle \bigoplus _{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D70B}^{\oplus 2\dim \text{LJ}(\unicode[STIX]{x1D70B})}\oplus \bigoplus _{\unicode[STIX]{x1D712}}(\text{St}\otimes (\unicode[STIX]{x1D712}\circ \det )),\nonumber\\ \displaystyle H_{\text{LT},\unicode[STIX]{x1D71B}}^{2} & \simeq & \displaystyle \bigoplus _{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D712}\circ \det )\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{\text{LT},\unicode[STIX]{x1D71B}}^{1} & \simeq & \displaystyle \bigoplus _{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D70B}^{\oplus 2\dim \text{LJ}(\unicode[STIX]{x1D70B})}\oplus \bigoplus _{\unicode[STIX]{x1D712}}(\text{St}\otimes (\unicode[STIX]{x1D712}\circ \det )),\nonumber\\ \displaystyle H_{\text{LT},\unicode[STIX]{x1D71B}}^{2} & \simeq & \displaystyle \bigoplus _{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D712}\circ \det )\nonumber\end{eqnarray}$$
as representations of
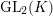 $\text{GL}_{2}(K)$
, where
$\text{GL}_{2}(K)$
, where
![]() $\unicode[STIX]{x1D70B}$
runs through irreducible cuspidal representations of
$\unicode[STIX]{x1D70B}$
runs through irreducible cuspidal representations of
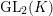 $\text{GL}_{2}(K)$
such that
$\text{GL}_{2}(K)$
such that
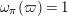 $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D71B})=1$
, and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D71B})=1$
, and
![]() $\unicode[STIX]{x1D712}$
runs through characters of
$\unicode[STIX]{x1D712}$
runs through characters of
![]() $K^{\times }$
satisfying
$K^{\times }$
satisfying
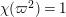 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{2})=1$
.
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{2})=1$
.
Proof. First, we show the second isomorphism. Let
![]() $\mathbf{X}(\mathfrak{p}^{n})$
be the connected Lubin–Tate curve with full level
$\mathbf{X}(\mathfrak{p}^{n})$
be the connected Lubin–Tate curve with full level
![]() $n$
over
$n$
over
![]() $\widehat{K}^{\text{ur}}$
(cf. [Reference StrauchSt2, 2.1]). We put
$\widehat{K}^{\text{ur}}$
(cf. [Reference StrauchSt2, 2.1]). We put
 $$\begin{eqnarray}\displaystyle H_{\mathbf{X}}^{2} & = & \displaystyle \varinjlim _{n}H_{\text{c}}^{2}(\mathbf{X}(\mathfrak{p}^{n})_{\mathbf{C}},\overline{\mathbb{Q}}_{\ell }),\nonumber\\ \displaystyle \text{GL}_{2}(K)^{0} & = & \displaystyle \{g\in \text{GL}_{2}(K)\mid \det g\in {\mathcal{O}}_{K}^{\times }\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{\mathbf{X}}^{2} & = & \displaystyle \varinjlim _{n}H_{\text{c}}^{2}(\mathbf{X}(\mathfrak{p}^{n})_{\mathbf{C}},\overline{\mathbb{Q}}_{\ell }),\nonumber\\ \displaystyle \text{GL}_{2}(K)^{0} & = & \displaystyle \{g\in \text{GL}_{2}(K)\mid \det g\in {\mathcal{O}}_{K}^{\times }\}.\nonumber\end{eqnarray}$$
Then,
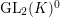 $\text{GL}_{2}(K)^{0}$
acts on
$\text{GL}_{2}(K)^{0}$
acts on
![]() $H_{\mathbf{X}}^{2}$
. By [Reference StrauchSt2, Theorem 4.4(i)], we have
$H_{\mathbf{X}}^{2}$
. By [Reference StrauchSt2, Theorem 4.4(i)], we have
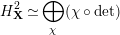 $$\begin{eqnarray}H_{\mathbf{X}}^{2}\simeq \bigoplus _{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D712}\circ \det )\end{eqnarray}$$
$$\begin{eqnarray}H_{\mathbf{X}}^{2}\simeq \bigoplus _{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D712}\circ \det )\end{eqnarray}$$
as representations of
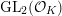 $\text{GL}_{2}({\mathcal{O}}_{K})$
, where
$\text{GL}_{2}({\mathcal{O}}_{K})$
, where
![]() $\unicode[STIX]{x1D712}$
runs through characters of
$\unicode[STIX]{x1D712}$
runs through characters of
![]() ${\mathcal{O}}_{K}^{\times }$
. Let
${\mathcal{O}}_{K}^{\times }$
. Let
![]() $H$
be the kernel of
$H$
be the kernel of
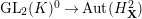 $\text{GL}_{2}(K)^{0}\rightarrow \text{Aut}(H_{\mathbf{X}}^{2})$
. Then,
$\text{GL}_{2}(K)^{0}\rightarrow \text{Aut}(H_{\mathbf{X}}^{2})$
. Then,
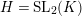 $H=\text{SL}_{2}(K)$
, because a normal subgroup of
$H=\text{SL}_{2}(K)$
, because a normal subgroup of
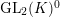 $\text{GL}_{2}(K)^{0}$
containing
$\text{GL}_{2}(K)^{0}$
containing
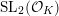 $\text{SL}_{2}({\mathcal{O}}_{K})$
is
$\text{SL}_{2}({\mathcal{O}}_{K})$
is
![]() $\text{SL}_{2}(K)$
by [Reference DeligneDe, Lemme 2.2.5(iii)]. Hence, we see that (2.1) is an isomorphism as representations of
$\text{SL}_{2}(K)$
by [Reference DeligneDe, Lemme 2.2.5(iii)]. Hence, we see that (2.1) is an isomorphism as representations of
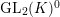 $\text{GL}_{2}(K)^{0}$
. The second isomorphism follows from this, because we have
$\text{GL}_{2}(K)^{0}$
. The second isomorphism follows from this, because we have
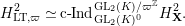 $$\begin{eqnarray}H_{\text{LT},\unicode[STIX]{x1D71B}}^{2}\simeq \text{c}\text{-}\text{Ind}_{\text{GL}_{2}(K)^{0}}^{\text{GL}_{2}(K)/\unicode[STIX]{x1D71B}^{\mathbb{Z}}}H_{\mathbf{X}}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}H_{\text{LT},\unicode[STIX]{x1D71B}}^{2}\simeq \text{c}\text{-}\text{Ind}_{\text{GL}_{2}(K)^{0}}^{\text{GL}_{2}(K)/\unicode[STIX]{x1D71B}^{\mathbb{Z}}}H_{\mathbf{X}}^{2}.\end{eqnarray}$$
Next, we show the first isomorphism. By [Reference MiedaMi, Definition 6.2 and Theorem 6.6], the cuspidal part of
![]() $H_{\text{LT},\unicode[STIX]{x1D71B}}^{1}$
is
$H_{\text{LT},\unicode[STIX]{x1D71B}}^{1}$
is
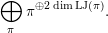 $$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D70B}^{\oplus 2\dim \text{LJ}(\unicode[STIX]{x1D70B})}.\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D70B}}\unicode[STIX]{x1D70B}^{\oplus 2\dim \text{LJ}(\unicode[STIX]{x1D70B})}.\end{eqnarray}$$
Here, we note that the characteristic of a local field is assumed to be zero in [Reference MiedaMi], but the same proof works in the equal characteristic case. By [Reference FarguesFar2, Théorème 4.3] and the Faltings–Fargues isomorphism (cf. [Reference FaltingsFal] and [Reference Fargues, Genestier and LafforgueFGL]), we see that the noncuspidal part of
![]() $H_{\text{LT},\unicode[STIX]{x1D71B}}^{1}$
is the Zelevinsky dual of
$H_{\text{LT},\unicode[STIX]{x1D71B}}^{1}$
is the Zelevinsky dual of
![]() $H_{\text{LT},\unicode[STIX]{x1D71B}}^{2}$
. Therefore, we have the first isomorphism.◻
$H_{\text{LT},\unicode[STIX]{x1D71B}}^{2}$
. Therefore, we have the first isomorphism.◻
3 Stable covering of Lubin–Tate curve with level two
In this section, we construct a stable covering of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{2})$
. Let
$\mathbf{X}_{1}(\mathfrak{p}^{2})$
. Let
![]() $(u,X_{2})$
be the parameter of
$(u,X_{2})$
be the parameter of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{2})$
given by the identification (1.4).
$\mathbf{X}_{1}(\mathfrak{p}^{2})$
given by the identification (1.4).
Let
![]() $\mathbf{Y}_{1,1}$
,
$\mathbf{Y}_{1,1}$
,
![]() $\mathbf{W}_{0}$
,
$\mathbf{W}_{0}$
,
![]() $\mathbf{W}_{k^{\times }}$
,
$\mathbf{W}_{k^{\times }}$
,
![]() $\mathbf{W}_{\infty ,1}$
,
$\mathbf{W}_{\infty ,1}$
,
![]() $\mathbf{W}_{\infty ,2}$
and
$\mathbf{W}_{\infty ,2}$
and
![]() $\mathbf{W}_{\infty ,3}$
be the subspaces of
$\mathbf{W}_{\infty ,3}$
be the subspaces of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{2})$
defined by the following conditions.
$\mathbf{X}_{1}(\mathfrak{p}^{2})$
defined by the following conditions.
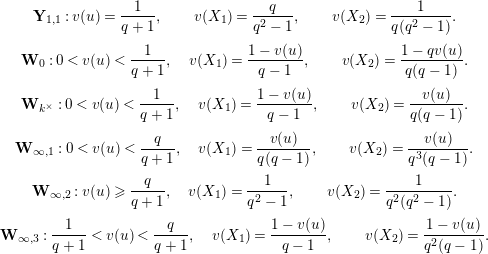 $$\begin{eqnarray}\displaystyle & \displaystyle \mathbf{Y}_{1,1}:v(u)={\displaystyle \frac{1}{q+1}},\qquad v(X_{1})={\displaystyle \frac{q}{q^{2}-1}},\qquad v(X_{2})={\displaystyle \frac{1}{q(q^{2}-1)}}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{W}_{0}:0<v(u)<{\displaystyle \frac{1}{q+1}},\quad v(X_{1})={\displaystyle \frac{1-v(u)}{q-1}},\qquad v(X_{2})={\displaystyle \frac{1-qv(u)}{q(q-1)}}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{W}_{k^{\times }}:0<v(u)<{\displaystyle \frac{1}{q+1}},\quad v(X_{1})={\displaystyle \frac{1-v(u)}{q-1}},\qquad v(X_{2})={\displaystyle \frac{v(u)}{q(q-1)}}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{W}_{\infty ,1}:0<v(u)<{\displaystyle \frac{q}{q+1}},\quad v(X_{1})={\displaystyle \frac{v(u)}{q(q-1)}},\qquad v(X_{2})={\displaystyle \frac{v(u)}{q^{3}(q-1)}}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{W}_{\infty ,2}:v(u)\geqslant {\displaystyle \frac{q}{q+1}},\quad v(X_{1})={\displaystyle \frac{1}{q^{2}-1}},\qquad v(X_{2})={\displaystyle \frac{1}{q^{2}(q^{2}-1)}}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{W}_{\infty ,3}:{\displaystyle \frac{1}{q+1}}<v(u)<{\displaystyle \frac{q}{q+1}},\quad v(X_{1})={\displaystyle \frac{1-v(u)}{q-1}},\qquad v(X_{2})={\displaystyle \frac{1-v(u)}{q^{2}(q-1)}}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathbf{Y}_{1,1}:v(u)={\displaystyle \frac{1}{q+1}},\qquad v(X_{1})={\displaystyle \frac{q}{q^{2}-1}},\qquad v(X_{2})={\displaystyle \frac{1}{q(q^{2}-1)}}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{W}_{0}:0<v(u)<{\displaystyle \frac{1}{q+1}},\quad v(X_{1})={\displaystyle \frac{1-v(u)}{q-1}},\qquad v(X_{2})={\displaystyle \frac{1-qv(u)}{q(q-1)}}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{W}_{k^{\times }}:0<v(u)<{\displaystyle \frac{1}{q+1}},\quad v(X_{1})={\displaystyle \frac{1-v(u)}{q-1}},\qquad v(X_{2})={\displaystyle \frac{v(u)}{q(q-1)}}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{W}_{\infty ,1}:0<v(u)<{\displaystyle \frac{q}{q+1}},\quad v(X_{1})={\displaystyle \frac{v(u)}{q(q-1)}},\qquad v(X_{2})={\displaystyle \frac{v(u)}{q^{3}(q-1)}}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{W}_{\infty ,2}:v(u)\geqslant {\displaystyle \frac{q}{q+1}},\quad v(X_{1})={\displaystyle \frac{1}{q^{2}-1}},\qquad v(X_{2})={\displaystyle \frac{1}{q^{2}(q^{2}-1)}}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{W}_{\infty ,3}:{\displaystyle \frac{1}{q+1}}<v(u)<{\displaystyle \frac{q}{q+1}},\quad v(X_{1})={\displaystyle \frac{1-v(u)}{q-1}},\qquad v(X_{2})={\displaystyle \frac{1-v(u)}{q^{2}(q-1)}}. & \displaystyle \nonumber\end{eqnarray}$$
We put
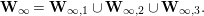 $$\begin{eqnarray}\mathbf{W}_{\infty }=\mathbf{W}_{\infty ,1}\cup \mathbf{W}_{\infty ,2}\cup \mathbf{W}_{\infty ,3}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{W}_{\infty }=\mathbf{W}_{\infty ,1}\cup \mathbf{W}_{\infty ,2}\cup \mathbf{W}_{\infty ,3}.\end{eqnarray}$$
Note that we have
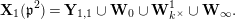 $$\begin{eqnarray}\mathbf{X}_{1}(\mathfrak{p}^{2})=\mathbf{Y}_{1,1}\cup \mathbf{W}_{0}\cup \mathbf{W}_{k^{\times }}^{1}\cup \mathbf{W}_{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{X}_{1}(\mathfrak{p}^{2})=\mathbf{Y}_{1,1}\cup \mathbf{W}_{0}\cup \mathbf{W}_{k^{\times }}^{1}\cup \mathbf{W}_{\infty }.\end{eqnarray}$$
Proposition 3.1. The Lubin–Tate curve
![]() $\mathbf{X}_{1}(\mathfrak{p}^{2})$
is a basic wide open space with underlying affinoid
$\mathbf{X}_{1}(\mathfrak{p}^{2})$
is a basic wide open space with underlying affinoid
![]() $\mathbf{Y}_{1,1}$
. Further,
$\mathbf{Y}_{1,1}$
. Further,
![]() $\mathbf{W}_{0}$
and
$\mathbf{W}_{0}$
and
![]() $\mathbf{W}_{\infty }$
are open annuli, and
$\mathbf{W}_{\infty }$
are open annuli, and
![]() $\mathbf{W}_{k^{\times }}$
is a disjoint union of
$\mathbf{W}_{k^{\times }}$
is a disjoint union of
![]() $q-1$
open annuli.
$q-1$
open annuli.
Proof. This is proved in [Reference Imai and TsushimaIT1] by direct calculations without cohomological arguments. Here, we sketch another proof based on arguments in this paper.
First, we note that
![]() ${\mathcal{X}}_{1}(1)$
is a good formal model of
${\mathcal{X}}_{1}(1)$
is a good formal model of
![]() $\mathbf{X}_{1}(1)$
. Then, we can show that
$\mathbf{X}_{1}(1)$
. Then, we can show that
![]() $\mathbf{X}_{1}(\mathfrak{p})$
is isomorphic to an open annulus by a cohomological argument as in the proof of Theorem 7.14 using the natural level-lowering map
$\mathbf{X}_{1}(\mathfrak{p})$
is isomorphic to an open annulus by a cohomological argument as in the proof of Theorem 7.14 using the natural level-lowering map
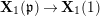 $\mathbf{X}_{1}(\mathfrak{p})\rightarrow \mathbf{X}_{1}(1)$
.
$\mathbf{X}_{1}(\mathfrak{p})\rightarrow \mathbf{X}_{1}(1)$
.
Next, we can see that the reduction of
![]() $\mathbf{Y}_{1,1}$
is isomorphic to the affine curve defined by
$\mathbf{Y}_{1,1}$
is isomorphic to the affine curve defined by
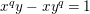 $x^{q}y-xy^{q}=1$
by a calculation as in the proof of Proposition 4.2 (cf. [Reference Imai and TsushimaIT1, Section 3.1]). Then, we can prove the claim by a similar argument to that above using the natural level-lowering map
$x^{q}y-xy^{q}=1$
by a calculation as in the proof of Proposition 4.2 (cf. [Reference Imai and TsushimaIT1, Section 3.1]). Then, we can prove the claim by a similar argument to that above using the natural level-lowering map
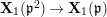 $\mathbf{X}_{1}(\mathfrak{p}^{2})\rightarrow \mathbf{X}_{1}(\mathfrak{p})$
.◻
$\mathbf{X}_{1}(\mathfrak{p}^{2})\rightarrow \mathbf{X}_{1}(\mathfrak{p})$
.◻
4 Reductions of affinoid spaces in
 $\mathbf{X}_{1}(\mathfrak{p}^{3})$
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
4.1 Definitions of several subspaces in
 $\mathbf{X}_{1}(\mathfrak{p}^{3})$
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
In this subsection, we define several subspaces of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
. Let
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
. Let
![]() $(u,X_{3})$
be the parameter of
$(u,X_{3})$
be the parameter of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
given by the identification (1.4).
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
given by the identification (1.4).
Let
![]() $\mathbf{Y}_{1,2}$
,
$\mathbf{Y}_{1,2}$
,
![]() $\mathbf{Y}_{2,1}$
and
$\mathbf{Y}_{2,1}$
and
![]() $\mathbf{Z}_{1,1}^{0}$
be the subspaces of
$\mathbf{Z}_{1,1}^{0}$
be the subspaces of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
defined by the following conditions.
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
defined by the following conditions.
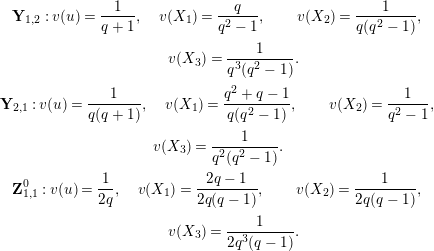 $$\begin{eqnarray}\displaystyle & \displaystyle \mathbf{Y}_{1,2}:v(u)={\displaystyle \frac{1}{q+1}},\quad v(X_{1})={\displaystyle \frac{q}{q^{2}-1}},\qquad v(X_{2})={\displaystyle \frac{1}{q(q^{2}-1)}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \qquad v(X_{3})={\displaystyle \frac{1}{q^{3}(q^{2}-1)}}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{Y}_{2,1}:v(u)={\displaystyle \frac{1}{q(q+1)}},\quad v(X_{1})={\displaystyle \frac{q^{2}+q-1}{q(q^{2}-1)}},\qquad v(X_{2})={\displaystyle \frac{1}{q^{2}-1}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle v(X_{3})={\displaystyle \frac{1}{q^{2}(q^{2}-1)}}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{Z}_{1,1}^{0}:v(u)={\displaystyle \frac{1}{2q}},\quad v(X_{1})={\displaystyle \frac{2q-1}{2q(q-1)}},\qquad v(X_{2})={\displaystyle \frac{1}{2q(q-1)}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \qquad v(X_{3})={\displaystyle \frac{1}{2q^{3}(q-1)}}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathbf{Y}_{1,2}:v(u)={\displaystyle \frac{1}{q+1}},\quad v(X_{1})={\displaystyle \frac{q}{q^{2}-1}},\qquad v(X_{2})={\displaystyle \frac{1}{q(q^{2}-1)}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \qquad v(X_{3})={\displaystyle \frac{1}{q^{3}(q^{2}-1)}}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{Y}_{2,1}:v(u)={\displaystyle \frac{1}{q(q+1)}},\quad v(X_{1})={\displaystyle \frac{q^{2}+q-1}{q(q^{2}-1)}},\qquad v(X_{2})={\displaystyle \frac{1}{q^{2}-1}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle v(X_{3})={\displaystyle \frac{1}{q^{2}(q^{2}-1)}}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{Z}_{1,1}^{0}:v(u)={\displaystyle \frac{1}{2q}},\quad v(X_{1})={\displaystyle \frac{2q-1}{2q(q-1)}},\qquad v(X_{2})={\displaystyle \frac{1}{2q(q-1)}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \qquad v(X_{3})={\displaystyle \frac{1}{2q^{3}(q-1)}}. & \displaystyle \nonumber\end{eqnarray}$$
We write down the following possible cases for
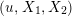 $(u,X_{1},X_{2})$
:
$(u,X_{1},X_{2})$
:
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}l@{}}(1)\quad 0<v(u)<{\displaystyle \frac{1}{q+1}},\quad v(X_{1})={\displaystyle \frac{1-v(u)}{q-1}},\qquad v(X_{2})={\displaystyle \frac{1-qv(u)}{q(q-1)}};\\ (2)\quad 0<v(u)<{\displaystyle \frac{1}{q+1}},\quad v(X_{1})={\displaystyle \frac{1-v(u)}{q-1}},\qquad v(X_{2})={\displaystyle \frac{v(u)}{q(q-1)}};\\ (3)\quad v(u)={\displaystyle \frac{1}{q+1}},\quad v(X_{1})={\displaystyle \frac{q}{q^{2}-1}},\qquad v(X_{2})={\displaystyle \frac{1}{q(q^{2}-1)}};\\ (4)\quad 0<v(u)<{\displaystyle \frac{q}{q+1}},\quad v(X_{1})={\displaystyle \frac{v(u)}{q(q-1)}},\qquad v(X_{2})={\displaystyle \frac{v(u)}{q^{3}(q-1)}};\\ (5)\quad v(u)\geqslant {\displaystyle \frac{q}{q+1}},\quad v(X_{1})={\displaystyle \frac{1}{q^{2}-1}},\qquad v(X_{2})={\displaystyle \frac{1}{q^{2}(q^{2}-1)}};\\ (6)\quad {\displaystyle \frac{1}{q+1}}<v(u)<{\displaystyle \frac{q}{q+1}},\quad v(X_{1})={\displaystyle \frac{1-v(u)}{q-1}},\qquad v(X_{2})={\displaystyle \frac{1-v(u)}{q^{2}(q-1)}}.\end{array} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}l@{}}(1)\quad 0<v(u)<{\displaystyle \frac{1}{q+1}},\quad v(X_{1})={\displaystyle \frac{1-v(u)}{q-1}},\qquad v(X_{2})={\displaystyle \frac{1-qv(u)}{q(q-1)}};\\ (2)\quad 0<v(u)<{\displaystyle \frac{1}{q+1}},\quad v(X_{1})={\displaystyle \frac{1-v(u)}{q-1}},\qquad v(X_{2})={\displaystyle \frac{v(u)}{q(q-1)}};\\ (3)\quad v(u)={\displaystyle \frac{1}{q+1}},\quad v(X_{1})={\displaystyle \frac{q}{q^{2}-1}},\qquad v(X_{2})={\displaystyle \frac{1}{q(q^{2}-1)}};\\ (4)\quad 0<v(u)<{\displaystyle \frac{q}{q+1}},\quad v(X_{1})={\displaystyle \frac{v(u)}{q(q-1)}},\qquad v(X_{2})={\displaystyle \frac{v(u)}{q^{3}(q-1)}};\\ (5)\quad v(u)\geqslant {\displaystyle \frac{q}{q+1}},\quad v(X_{1})={\displaystyle \frac{1}{q^{2}-1}},\qquad v(X_{2})={\displaystyle \frac{1}{q^{2}(q^{2}-1)}};\\ (6)\quad {\displaystyle \frac{1}{q+1}}<v(u)<{\displaystyle \frac{q}{q+1}},\quad v(X_{1})={\displaystyle \frac{1-v(u)}{q-1}},\qquad v(X_{2})={\displaystyle \frac{1-v(u)}{q^{2}(q-1)}}.\end{array} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Next, we consider the following possible cases for
 $(X_{2},X_{3})$
:
$(X_{2},X_{3})$
:
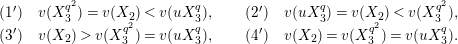 $$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}(1^{\prime })\quad v(X_{3}^{q^{2}})=v(X_{2})<v(uX_{3}^{q}),\qquad (2^{\prime })\quad v(uX_{3}^{q})=v(X_{2})<v(X_{3}^{q^{2}}),\\ (3^{\prime })\quad v(X_{2})>v(X_{3}^{q^{2}})=v(uX_{3}^{q}),\qquad (4^{\prime })\quad v(X_{2})=v(X_{3}^{q^{2}})=v(uX_{3}^{q}).\end{array} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}c@{}}(1^{\prime })\quad v(X_{3}^{q^{2}})=v(X_{2})<v(uX_{3}^{q}),\qquad (2^{\prime })\quad v(uX_{3}^{q})=v(X_{2})<v(X_{3}^{q^{2}}),\\ (3^{\prime })\quad v(X_{2})>v(X_{3}^{q^{2}})=v(uX_{3}^{q}),\qquad (4^{\prime })\quad v(X_{2})=v(X_{3}^{q^{2}})=v(uX_{3}^{q}).\end{array} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Lemma 4.1. For
 $2\leqslant i\leqslant 6$
in (4.1) and
$2\leqslant i\leqslant 6$
in (4.1) and
 $2^{\prime }\leqslant j^{\prime }\leqslant 4^{\prime }$
in (4.2), the case
$2^{\prime }\leqslant j^{\prime }\leqslant 4^{\prime }$
in (4.2), the case
![]() $i$
and
$i$
and
![]() $j^{\prime }$
does not happen.
$j^{\prime }$
does not happen.
Proof. This is an easy exercise. ◻
Let
![]() $\mathbf{W}_{i,j^{\prime }}$
be the subspace of
$\mathbf{W}_{i,j^{\prime }}$
be the subspace of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
defined by the conditions
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
defined by the conditions
 $1\leqslant i\leqslant 6$
in (4.1) and
$1\leqslant i\leqslant 6$
in (4.1) and
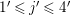 $1^{\prime }\leqslant j^{\prime }\leqslant 4^{\prime }$
in (4.2). We note that
$1^{\prime }\leqslant j^{\prime }\leqslant 4^{\prime }$
in (4.2). We note that
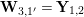 $\mathbf{W}_{3,1^{\prime }}=\mathbf{Y}_{1,2}$
and
$\mathbf{W}_{3,1^{\prime }}=\mathbf{Y}_{1,2}$
and
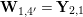 $\mathbf{W}_{1,4^{\prime }}=\mathbf{Y}_{2,1}$
. Let
$\mathbf{W}_{1,4^{\prime }}=\mathbf{Y}_{2,1}$
. Let
![]() $\mathbf{W}_{1,1^{\prime }}^{+}$
and
$\mathbf{W}_{1,1^{\prime }}^{+}$
and
![]() $\mathbf{W}_{1,1^{\prime }}^{-}$
be the subspaces of
$\mathbf{W}_{1,1^{\prime }}^{-}$
be the subspaces of
![]() $\mathbf{W}_{1,1^{\prime }}$
defined by
$\mathbf{W}_{1,1^{\prime }}$
defined by
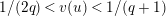 $1/(2q)<v(u)<1/(q+1)$
and
$1/(2q)<v(u)<1/(q+1)$
and
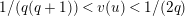 $1/(q(q+1))<v(u)<1/(2q)$
respectively.
$1/(q(q+1))<v(u)<1/(2q)$
respectively.
4.2 Reductions of the affinoid spaces
 $\mathbf{Y}_{1,2}$
and
$\mathbf{Y}_{1,2}$
and
 $\mathbf{Y}_{2,1}$
$\mathbf{Y}_{2,1}$
In this subsection, we compute the reductions of the affinoid spaces
![]() $\mathbf{Y}_{1,2}$
and
$\mathbf{Y}_{1,2}$
and
![]() $\mathbf{Y}_{2,1}$
. The reductions of
$\mathbf{Y}_{2,1}$
. The reductions of
![]() $\mathbf{Y}_{2,1}$
and
$\mathbf{Y}_{2,1}$
and
![]() $\mathbf{Y}_{1,2}$
are isomorphic to the affine curve defined by
$\mathbf{Y}_{1,2}$
are isomorphic to the affine curve defined by
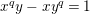 $x^{q}y-xy^{q}=1$
. These curves have genus
$x^{q}y-xy^{q}=1$
. These curves have genus
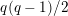 $q(q-1)/2$
.
$q(q-1)/2$
.
Proposition 4.2. The reduction of
![]() $\mathbf{Y}_{1,2}$
is isomorphic to the affine curve defined by
$\mathbf{Y}_{1,2}$
is isomorphic to the affine curve defined by
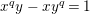 $x^{q}y-xy^{q}=1$
.
$x^{q}y-xy^{q}=1$
.
Proof. We change variables as
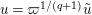 $u=\unicode[STIX]{x1D71B}^{1/(q+1)}\tilde{u}$
,
$u=\unicode[STIX]{x1D71B}^{1/(q+1)}\tilde{u}$
,
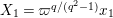 $X_{1}=\unicode[STIX]{x1D71B}^{q/(q^{2}-1)}x_{1}$
,
$X_{1}=\unicode[STIX]{x1D71B}^{q/(q^{2}-1)}x_{1}$
,
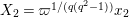 $X_{2}=\unicode[STIX]{x1D71B}^{1/(q(q^{2}-1))}x_{2}$
and
$X_{2}=\unicode[STIX]{x1D71B}^{1/(q(q^{2}-1))}x_{2}$
and
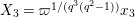 $X_{3}=\unicode[STIX]{x1D71B}^{1/(q^{3}(q^{2}-1))}x_{3}$
. By Lemma 1.1, we have
$X_{3}=\unicode[STIX]{x1D71B}^{1/(q^{3}(q^{2}-1))}x_{3}$
. By Lemma 1.1, we have
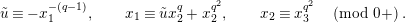 $$\begin{eqnarray}\tilde{u} \equiv -x_{1}^{-(q-1)},\qquad x_{1}\equiv \tilde{u} x_{2}^{q}+x_{2}^{q^{2}},\qquad x_{2}\equiv x_{3}^{q^{2}}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{u} \equiv -x_{1}^{-(q-1)},\qquad x_{1}\equiv \tilde{u} x_{2}^{q}+x_{2}^{q^{2}},\qquad x_{2}\equiv x_{3}^{q^{2}}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
Then, we have
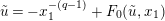 $\tilde{u} =-x_{1}^{-(q-1)}+F_{0}(\tilde{u} ,x_{1})$
for some function
$\tilde{u} =-x_{1}^{-(q-1)}+F_{0}(\tilde{u} ,x_{1})$
for some function
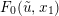 $F_{0}(\tilde{u} ,x_{1})$
satisfying
$F_{0}(\tilde{u} ,x_{1})$
satisfying
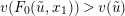 $v(F_{0}(\tilde{u} ,x_{1}))>v(\tilde{u} )$
. Substituting
$v(F_{0}(\tilde{u} ,x_{1}))>v(\tilde{u} )$
. Substituting
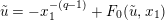 $\tilde{u} =-x_{1}^{-(q-1)}+F_{0}(\tilde{u} ,x_{1})$
into
$\tilde{u} =-x_{1}^{-(q-1)}+F_{0}(\tilde{u} ,x_{1})$
into
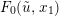 $F_{0}(\tilde{u} ,x_{1})$
and repeating it, we see that
$F_{0}(\tilde{u} ,x_{1})$
and repeating it, we see that
![]() $\tilde{u}$
is written as a function of
$\tilde{u}$
is written as a function of
![]() $x_{1}$
. Similarly, by
$x_{1}$
. Similarly, by
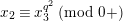 $x_{2}\equiv x_{3}^{q^{2}}\;(\text{mod}~0+)$
, we can see that
$x_{2}\equiv x_{3}^{q^{2}}\;(\text{mod}~0+)$
, we can see that
![]() $x_{2}$
is written as a function of
$x_{2}$
is written as a function of
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{3}$
. By (4.3), we acquire
$x_{3}$
. By (4.3), we acquire
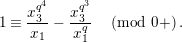 $$\begin{eqnarray}1\equiv {\displaystyle \frac{x_{3}^{q^{4}}}{x_{1}}}-{\displaystyle \frac{x_{3}^{q^{3}}}{x_{1}^{q}}}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
$$\begin{eqnarray}1\equiv {\displaystyle \frac{x_{3}^{q^{4}}}{x_{1}}}-{\displaystyle \frac{x_{3}^{q^{3}}}{x_{1}^{q}}}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
By setting
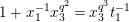 $1+x_{1}^{-1}x_{3}^{q^{2}}=x_{3}^{q^{3}}t_{1}^{-1}$
and substituting this into (4.4), we obtain
$1+x_{1}^{-1}x_{3}^{q^{2}}=x_{3}^{q^{3}}t_{1}^{-1}$
and substituting this into (4.4), we obtain
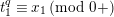 $t_{1}^{q}\equiv x_{1}\;(\text{mod}~0+)$
and hence
$t_{1}^{q}\equiv x_{1}\;(\text{mod}~0+)$
and hence
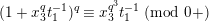 $(1+x_{3}^{q}t_{1}^{-1})^{q}\equiv x_{3}^{q^{3}}t_{1}^{-1}\;(\text{mod}~0+)$
. By setting
$(1+x_{3}^{q}t_{1}^{-1})^{q}\equiv x_{3}^{q^{3}}t_{1}^{-1}\;(\text{mod}~0+)$
. By setting
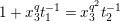 $1+x_{3}^{q}t_{1}^{-1}=x_{3}^{q^{2}}t_{2}^{-1}$
, we obtain
$1+x_{3}^{q}t_{1}^{-1}=x_{3}^{q^{2}}t_{2}^{-1}$
, we obtain
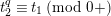 $t_{2}^{q}\equiv t_{1}\;(\text{mod}~0+)$
. Hence,
$t_{2}^{q}\equiv t_{1}\;(\text{mod}~0+)$
. Hence,
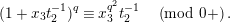 $$\begin{eqnarray}(1+x_{3}t_{2}^{-1})^{q}\equiv x_{3}^{q^{2}}t_{2}^{-1}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
$$\begin{eqnarray}(1+x_{3}t_{2}^{-1})^{q}\equiv x_{3}^{q^{2}}t_{2}^{-1}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
Finally, by setting
![]() $x=x_{3}$
and
$x=x_{3}$
and
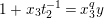 $1+x_{3}t_{2}^{-1}=x_{3}^{q}y$
, we acquire
$1+x_{3}t_{2}^{-1}=x_{3}^{q}y$
, we acquire
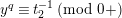 $y^{q}\equiv t_{2}^{-1}\;(\text{mod}~0+)$
. Hence, we have
$y^{q}\equiv t_{2}^{-1}\;(\text{mod}~0+)$
. Hence, we have
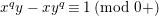 $x^{q}y-xy^{q}\equiv 1\;(\text{mod}~0+)$
. Note that
$x^{q}y-xy^{q}\equiv 1\;(\text{mod}~0+)$
. Note that
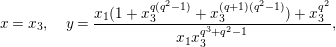 $$\begin{eqnarray}x=x_{3},\quad y={\displaystyle \frac{x_{1}(1+x_{3}^{q(q^{2}-1)}+x_{3}^{(q+1)(q^{2}-1)})+x_{3}^{q^{2}}}{x_{1}x_{3}^{q^{3}+q^{2}-1}}},\end{eqnarray}$$
$$\begin{eqnarray}x=x_{3},\quad y={\displaystyle \frac{x_{1}(1+x_{3}^{q(q^{2}-1)}+x_{3}^{(q+1)(q^{2}-1)})+x_{3}^{q^{2}}}{x_{1}x_{3}^{q^{3}+q^{2}-1}}},\end{eqnarray}$$
which we will use later. ◻
We put
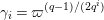 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{i}=\unicode[STIX]{x1D71B}^{(q-1)/(2q^{i})}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{i}=\unicode[STIX]{x1D71B}^{(q-1)/(2q^{i})}\end{eqnarray}$$
for
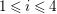 $1\leqslant i\leqslant 4$
. We choose an element
$1\leqslant i\leqslant 4$
. We choose an element
![]() $c_{0}$
such that
$c_{0}$
such that
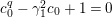 $c_{0}^{q}-\unicode[STIX]{x1D6FE}_{1}^{2}c_{0}+1=0$
. Note that we have
$c_{0}^{q}-\unicode[STIX]{x1D6FE}_{1}^{2}c_{0}+1=0$
. Note that we have
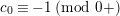 $c_{0}\equiv -1\;(\text{mod}~0+)$
. Further, we choose a
$c_{0}\equiv -1\;(\text{mod}~0+)$
. Further, we choose a
![]() $q$
th root
$q$
th root
![]() $c_{0}^{1/q}$
of
$c_{0}^{1/q}$
of
![]() $c_{0}$
.
$c_{0}$
.
Proposition 4.3. The reduction of the space
![]() $\mathbf{Y}_{2,1}$
is isomorphic to the affine curve defined by
$\mathbf{Y}_{2,1}$
is isomorphic to the affine curve defined by
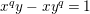 $x^{q}y-xy^{q}=1$
.
$x^{q}y-xy^{q}=1$
.
Proof. We change variables as
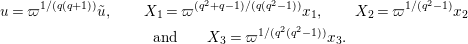 $$\begin{eqnarray}\displaystyle & \displaystyle u=\unicode[STIX]{x1D71B}^{1/(q(q+1))}\tilde{u} ,\qquad X_{1}=\unicode[STIX]{x1D71B}^{(q^{2}+q-1)/(q(q^{2}-1))}x_{1},\qquad X_{2}=\unicode[STIX]{x1D71B}^{1/(q^{2}-1)}x_{2} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \qquad \text{and}\qquad X_{3}=\unicode[STIX]{x1D71B}^{1/(q^{2}(q^{2}-1))}x_{3}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u=\unicode[STIX]{x1D71B}^{1/(q(q+1))}\tilde{u} ,\qquad X_{1}=\unicode[STIX]{x1D71B}^{(q^{2}+q-1)/(q(q^{2}-1))}x_{1},\qquad X_{2}=\unicode[STIX]{x1D71B}^{1/(q^{2}-1)}x_{2} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \qquad \text{and}\qquad X_{3}=\unicode[STIX]{x1D71B}^{1/(q^{2}(q^{2}-1))}x_{3}. & \displaystyle \nonumber\end{eqnarray}$$
By Lemma 1.1, we have
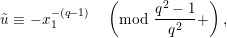 $$\begin{eqnarray}\displaystyle \tilde{u} & \equiv & \displaystyle -x_{1}^{-(q-1)}\quad \left(\text{mod}~{\displaystyle \frac{q^{2}-1}{q^{2}}}+\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{u} & \equiv & \displaystyle -x_{1}^{-(q-1)}\quad \left(\text{mod}~{\displaystyle \frac{q^{2}-1}{q^{2}}}+\right),\end{eqnarray}$$
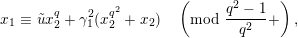 $$\begin{eqnarray}\displaystyle x_{1} & \equiv & \displaystyle \tilde{u} x_{2}^{q}+\unicode[STIX]{x1D6FE}_{1}^{2}(x_{2}^{q^{2}}+x_{2})\quad \left(\text{mod}~{\displaystyle \frac{q^{2}-1}{q^{2}}}+\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{1} & \equiv & \displaystyle \tilde{u} x_{2}^{q}+\unicode[STIX]{x1D6FE}_{1}^{2}(x_{2}^{q^{2}}+x_{2})\quad \left(\text{mod}~{\displaystyle \frac{q^{2}-1}{q^{2}}}+\right),\end{eqnarray}$$
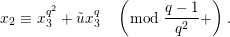 $$\begin{eqnarray}\displaystyle x_{2} & \equiv & \displaystyle x_{3}^{q^{2}}+\tilde{u} x_{3}^{q}\quad \left(\text{mod}~{\displaystyle \frac{q-1}{q^{2}}}+\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{2} & \equiv & \displaystyle x_{3}^{q^{2}}+\tilde{u} x_{3}^{q}\quad \left(\text{mod}~{\displaystyle \frac{q-1}{q^{2}}}+\right).\end{eqnarray}$$
By (4.6) and (4.8), we can see that
![]() $\tilde{u}$
is written as a function of
$\tilde{u}$
is written as a function of
![]() $x_{1}$
, and that
$x_{1}$
, and that
![]() $x_{2}$
is written as a function of
$x_{2}$
is written as a function of
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{3}$
. We define a parameter
$x_{3}$
. We define a parameter
![]() $t$
by
$t$
by
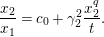 $$\begin{eqnarray}{\displaystyle \frac{x_{2}}{x_{1}}}=c_{0}+\unicode[STIX]{x1D6FE}_{2}^{2}{\displaystyle \frac{x_{2}^{q}}{t}}.\end{eqnarray}$$
$$\begin{eqnarray}{\displaystyle \frac{x_{2}}{x_{1}}}=c_{0}+\unicode[STIX]{x1D6FE}_{2}^{2}{\displaystyle \frac{x_{2}^{q}}{t}}.\end{eqnarray}$$
We note that
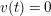 $v(t)=0$
. By considering
$v(t)=0$
. By considering
![]() $x_{1}^{-1}\times$
(4.7), we have
$x_{1}^{-1}\times$
(4.7), we have
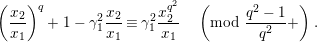 $$\begin{eqnarray}\biggl({\displaystyle \frac{x_{2}}{x_{1}}}\biggr)^{q}+1-\unicode[STIX]{x1D6FE}_{1}^{2}{\displaystyle \frac{x_{2}}{x_{1}}}\equiv \unicode[STIX]{x1D6FE}_{1}^{2}{\displaystyle \frac{x_{2}^{q^{2}}}{x_{1}}}\quad \left(\text{mod}~{\displaystyle \frac{q^{2}-1}{q^{2}}}+\right).\end{eqnarray}$$
$$\begin{eqnarray}\biggl({\displaystyle \frac{x_{2}}{x_{1}}}\biggr)^{q}+1-\unicode[STIX]{x1D6FE}_{1}^{2}{\displaystyle \frac{x_{2}}{x_{1}}}\equiv \unicode[STIX]{x1D6FE}_{1}^{2}{\displaystyle \frac{x_{2}^{q^{2}}}{x_{1}}}\quad \left(\text{mod}~{\displaystyle \frac{q^{2}-1}{q^{2}}}+\right).\end{eqnarray}$$
By substituting (4.9) into the left-hand side of the congruence (4.10), and dividing it by
![]() $\unicode[STIX]{x1D6FE}_{1}^{2}x_{2}^{q^{2}}$
, we acquire
$\unicode[STIX]{x1D6FE}_{1}^{2}x_{2}^{q^{2}}$
, we acquire
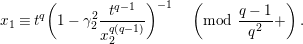 $$\begin{eqnarray}x_{1}\equiv t^{q}\biggl(1-\unicode[STIX]{x1D6FE}_{2}^{2}{\displaystyle \frac{t^{q-1}}{x_{2}^{q(q-1)}}}\biggr)^{-1}\quad \left(\text{mod}~{\displaystyle \frac{q-1}{q^{2}}}+\right).\end{eqnarray}$$
$$\begin{eqnarray}x_{1}\equiv t^{q}\biggl(1-\unicode[STIX]{x1D6FE}_{2}^{2}{\displaystyle \frac{t^{q-1}}{x_{2}^{q(q-1)}}}\biggr)^{-1}\quad \left(\text{mod}~{\displaystyle \frac{q-1}{q^{2}}}+\right).\end{eqnarray}$$
By this congruence, we can see that
![]() $x_{1}$
is written as a function of
$x_{1}$
is written as a function of
![]() $t$
and
$t$
and
![]() $x_{3}$
. By considering
$x_{3}$
. By considering
![]() $x_{1}^{-1}\times$
(4.8), we acquire
$x_{1}^{-1}\times$
(4.8), we acquire
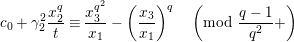 $$\begin{eqnarray}c_{0}+\unicode[STIX]{x1D6FE}_{2}^{2}{\displaystyle \frac{x_{2}^{q}}{t}}\equiv {\displaystyle \frac{x_{3}^{q^{2}}}{x_{1}}}-\biggl({\displaystyle \frac{x_{3}}{x_{1}}}\biggr)^{q}\quad \left(\text{mod}~{\displaystyle \frac{q-1}{q^{2}}}+\right)\end{eqnarray}$$
$$\begin{eqnarray}c_{0}+\unicode[STIX]{x1D6FE}_{2}^{2}{\displaystyle \frac{x_{2}^{q}}{t}}\equiv {\displaystyle \frac{x_{3}^{q^{2}}}{x_{1}}}-\biggl({\displaystyle \frac{x_{3}}{x_{1}}}\biggr)^{q}\quad \left(\text{mod}~{\displaystyle \frac{q-1}{q^{2}}}+\right)\end{eqnarray}$$
by (4.9). Substituting (4.11) into (4.12), we have
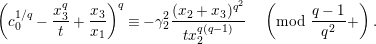 $$\begin{eqnarray}\biggl(c_{0}^{1/q}-{\displaystyle \frac{x_{3}^{q}}{t}}+{\displaystyle \frac{x_{3}}{x_{1}}}\biggr)^{q}\equiv -\unicode[STIX]{x1D6FE}_{2}^{2}{\displaystyle \frac{(x_{2}+x_{3})^{q^{2}}}{tx_{2}^{q(q-1)}}}\quad \left(\text{mod}~{\displaystyle \frac{q-1}{q^{2}}}+\right).\end{eqnarray}$$
$$\begin{eqnarray}\biggl(c_{0}^{1/q}-{\displaystyle \frac{x_{3}^{q}}{t}}+{\displaystyle \frac{x_{3}}{x_{1}}}\biggr)^{q}\equiv -\unicode[STIX]{x1D6FE}_{2}^{2}{\displaystyle \frac{(x_{2}+x_{3})^{q^{2}}}{tx_{2}^{q(q-1)}}}\quad \left(\text{mod}~{\displaystyle \frac{q-1}{q^{2}}}+\right).\end{eqnarray}$$
By (4.9) and
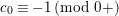 $c_{0}\equiv -1\;(\text{mod}~0+)$
, we have
$c_{0}\equiv -1\;(\text{mod}~0+)$
, we have
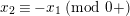 $x_{2}\equiv -x_{1}\;(\text{mod}~0+)$
. Therefore, we acquire
$x_{2}\equiv -x_{1}\;(\text{mod}~0+)$
. Therefore, we acquire
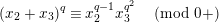 $$\begin{eqnarray}(x_{2}+x_{3})^{q}\equiv x_{2}^{q-1}x_{3}^{q^{2}}\quad \left(\text{mod}~0+\right)\end{eqnarray}$$
$$\begin{eqnarray}(x_{2}+x_{3})^{q}\equiv x_{2}^{q-1}x_{3}^{q^{2}}\quad \left(\text{mod}~0+\right)\end{eqnarray}$$
by (4.6) and (4.8). In particular, we obtain
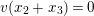 $v(x_{2}+x_{3})=0$
. We introduce a new parameter
$v(x_{2}+x_{3})=0$
. We introduce a new parameter
![]() $t_{1}$
as
$t_{1}$
as
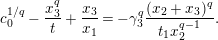 $$\begin{eqnarray}c_{0}^{1/q}-{\displaystyle \frac{x_{3}^{q}}{t}}+{\displaystyle \frac{x_{3}}{x_{1}}}=-\unicode[STIX]{x1D6FE}_{3}^{q}{\displaystyle \frac{(x_{2}+x_{3})^{q}}{t_{1}x_{2}^{q-1}}}.\end{eqnarray}$$
$$\begin{eqnarray}c_{0}^{1/q}-{\displaystyle \frac{x_{3}^{q}}{t}}+{\displaystyle \frac{x_{3}}{x_{1}}}=-\unicode[STIX]{x1D6FE}_{3}^{q}{\displaystyle \frac{(x_{2}+x_{3})^{q}}{t_{1}x_{2}^{q-1}}}.\end{eqnarray}$$
Substituting this into the left-hand side of the congruence (4.13), and dividing it by
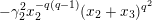 $-\unicode[STIX]{x1D6FE}_{2}^{2}x_{2}^{-q(q-1)}(x_{2}+x_{3})^{q^{2}}$
, we acquire
$-\unicode[STIX]{x1D6FE}_{2}^{2}x_{2}^{-q(q-1)}(x_{2}+x_{3})^{q^{2}}$
, we acquire
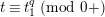 $t\equiv t_{1}^{q}\;(\text{mod}~0+)$
. By this congruence, we can see that
$t\equiv t_{1}^{q}\;(\text{mod}~0+)$
. By this congruence, we can see that
![]() $t$
is written as a function of
$t$
is written as a function of
![]() $t_{1}$
and
$t_{1}$
and
![]() $x_{3}$
. By (4.14), we obtain
$x_{3}$
. By (4.14), we obtain
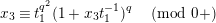 $$\begin{eqnarray}x_{3}\equiv t_{1}^{q^{2}}(1+x_{3}t_{1}^{-1})^{q}\quad \left(\text{mod}~0+\right)\end{eqnarray}$$
$$\begin{eqnarray}x_{3}\equiv t_{1}^{q^{2}}(1+x_{3}t_{1}^{-1})^{q}\quad \left(\text{mod}~0+\right)\end{eqnarray}$$
using
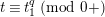 $t\equiv t_{1}^{q}\;(\text{mod}~0+)$
and
$t\equiv t_{1}^{q}\;(\text{mod}~0+)$
and
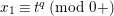 $x_{1}\equiv t^{q}\;(\text{mod}~0+)$
. Hence, by setting
$x_{1}\equiv t^{q}\;(\text{mod}~0+)$
. Hence, by setting
![]() $x=t_{1}^{-1}$
and
$x=t_{1}^{-1}$
and
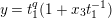 $~y=t_{1}^{q}(1+x_{3}t_{1}^{-1})$
, we acquire
$~y=t_{1}^{q}(1+x_{3}t_{1}^{-1})$
, we acquire
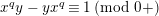 $x^{q}y-yx^{q}\equiv 1\;(\text{mod}~0+)$
.◻
$x^{q}y-yx^{q}\equiv 1\;(\text{mod}~0+)$
.◻
4.3 Reduction of the affinoid space
 $\mathbf{Z}_{1,1}^{0}$
$\mathbf{Z}_{1,1}^{0}$
In this subsection, we calculate the reduction of the affinoid space
![]() $\mathbf{Z}_{1,1}^{0}$
. We define
$\mathbf{Z}_{1,1}^{0}$
. We define
![]() ${\mathcal{S}}_{1}$
as in the introduction. The reduction
${\mathcal{S}}_{1}$
as in the introduction. The reduction
![]() $\overline{\mathbf{Z}}_{1,1}^{0}$
is isomorphic to the affine curve defined by
$\overline{\mathbf{Z}}_{1,1}^{0}$
is isomorphic to the affine curve defined by
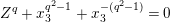 $Z^{q}+x_{3}^{q^{2}-1}+x_{3}^{-(q^{2}-1)}=0$
. This affine curve has genus
$Z^{q}+x_{3}^{q^{2}-1}+x_{3}^{-(q^{2}-1)}=0$
. This affine curve has genus
![]() $0$
and singularities at
$0$
and singularities at
![]() $x_{3}\in {\mathcal{S}}_{1}$
.
$x_{3}\in {\mathcal{S}}_{1}$
.
We put
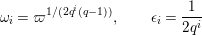 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D71B}^{1/(2q^{i}(q-1))},\qquad \unicode[STIX]{x1D716}_{i}={\displaystyle \frac{1}{2q^{i}}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D71B}^{1/(2q^{i}(q-1))},\qquad \unicode[STIX]{x1D716}_{i}={\displaystyle \frac{1}{2q^{i}}}\end{eqnarray}$$
for
 $1\leqslant i\leqslant 4$
. We change variables as
$1\leqslant i\leqslant 4$
. We change variables as
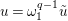 $u=\unicode[STIX]{x1D714}_{1}^{q-1}\tilde{u}$
,
$u=\unicode[STIX]{x1D714}_{1}^{q-1}\tilde{u}$
,
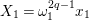 $X_{1}=\unicode[STIX]{x1D714}_{1}^{2q-1}x_{1}$
,
$X_{1}=\unicode[STIX]{x1D714}_{1}^{2q-1}x_{1}$
,
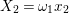 $X_{2}=\unicode[STIX]{x1D714}_{1}x_{2}$
and
$X_{2}=\unicode[STIX]{x1D714}_{1}x_{2}$
and
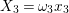 $X_{3}=\unicode[STIX]{x1D714}_{3}x_{3}$
. By Lemma 1.1, we have
$X_{3}=\unicode[STIX]{x1D714}_{3}x_{3}$
. By Lemma 1.1, we have
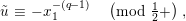 $$\begin{eqnarray}\displaystyle \tilde{u} & \equiv & \displaystyle -x_{1}^{-(q-1)}\quad \left(\text{mod}~{\textstyle \frac{1}{2}}+\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{u} & \equiv & \displaystyle -x_{1}^{-(q-1)}\quad \left(\text{mod}~{\textstyle \frac{1}{2}}+\right),\end{eqnarray}$$
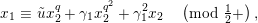 $$\begin{eqnarray}\displaystyle x_{1} & \equiv & \displaystyle \tilde{u} x_{2}^{q}+\unicode[STIX]{x1D6FE}_{1}x_{2}^{q^{2}}+\unicode[STIX]{x1D6FE}_{1}^{2}x_{2}\quad \left(\text{mod}~{\textstyle \frac{1}{2}}+\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{1} & \equiv & \displaystyle \tilde{u} x_{2}^{q}+\unicode[STIX]{x1D6FE}_{1}x_{2}^{q^{2}}+\unicode[STIX]{x1D6FE}_{1}^{2}x_{2}\quad \left(\text{mod}~{\textstyle \frac{1}{2}}+\right),\end{eqnarray}$$
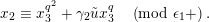 $$\begin{eqnarray}\displaystyle x_{2} & \equiv & \displaystyle x_{3}^{q^{2}}+\unicode[STIX]{x1D6FE}_{2}\tilde{u} x_{3}^{q}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{2} & \equiv & \displaystyle x_{3}^{q^{2}}+\unicode[STIX]{x1D6FE}_{2}\tilde{u} x_{3}^{q}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right).\end{eqnarray}$$
Note that we have
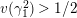 $v(\unicode[STIX]{x1D6FE}_{1}^{2})>1/2$
if
$v(\unicode[STIX]{x1D6FE}_{1}^{2})>1/2$
if
![]() $q\neq 2$
. By (4.15) and (4.17), we can see that
$q\neq 2$
. By (4.15) and (4.17), we can see that
![]() $\tilde{u}$
is written as a function of
$\tilde{u}$
is written as a function of
![]() $x_{1}$
, and that
$x_{1}$
, and that
![]() $x_{2}$
is written as a function of
$x_{2}$
is written as a function of
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{3}$
. We define a parameter
$x_{3}$
. We define a parameter
![]() $t$
by
$t$
by
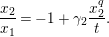 $$\begin{eqnarray}{\displaystyle \frac{x_{2}}{x_{1}}}=-1+\unicode[STIX]{x1D6FE}_{2}{\displaystyle \frac{x_{2}^{q}}{t}}.\end{eqnarray}$$
$$\begin{eqnarray}{\displaystyle \frac{x_{2}}{x_{1}}}=-1+\unicode[STIX]{x1D6FE}_{2}{\displaystyle \frac{x_{2}^{q}}{t}}.\end{eqnarray}$$
By considering
![]() $x_{1}^{-1}\times$
(4.16), we acquire
$x_{1}^{-1}\times$
(4.16), we acquire
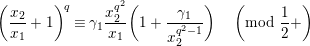 $$\begin{eqnarray}\biggl({\displaystyle \frac{x_{2}}{x_{1}}}+1\biggr)^{q}\equiv \unicode[STIX]{x1D6FE}_{1}{\displaystyle \frac{x_{2}^{q^{2}}}{x_{1}}}\biggl(1+{\displaystyle \frac{\unicode[STIX]{x1D6FE}_{1}}{x_{2}^{q^{2}-1}}}\biggr)\quad \left(\text{mod}~{\displaystyle \frac{1}{2}}+\right)\end{eqnarray}$$
$$\begin{eqnarray}\biggl({\displaystyle \frac{x_{2}}{x_{1}}}+1\biggr)^{q}\equiv \unicode[STIX]{x1D6FE}_{1}{\displaystyle \frac{x_{2}^{q^{2}}}{x_{1}}}\biggl(1+{\displaystyle \frac{\unicode[STIX]{x1D6FE}_{1}}{x_{2}^{q^{2}-1}}}\biggr)\quad \left(\text{mod}~{\displaystyle \frac{1}{2}}+\right)\end{eqnarray}$$
by (4.15). Substituting (4.18) into (4.19), and dividing it by
![]() $\unicode[STIX]{x1D6FE}_{1}x_{2}^{q^{2}}$
, we obtain
$\unicode[STIX]{x1D6FE}_{1}x_{2}^{q^{2}}$
, we obtain
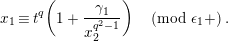 $$\begin{eqnarray}x_{1}\equiv t^{q}\biggl(1+{\displaystyle \frac{\unicode[STIX]{x1D6FE}_{1}}{x_{2}^{q^{2}-1}}}\biggr)\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right).\end{eqnarray}$$
$$\begin{eqnarray}x_{1}\equiv t^{q}\biggl(1+{\displaystyle \frac{\unicode[STIX]{x1D6FE}_{1}}{x_{2}^{q^{2}-1}}}\biggr)\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right).\end{eqnarray}$$
Therefore, we have
 $v(t)=0$
. By considering
$v(t)=0$
. By considering
![]() $x_{1}^{-1}\times$
(4.17), we acquire
$x_{1}^{-1}\times$
(4.17), we acquire
 $$\begin{eqnarray}\biggl(1+{\displaystyle \frac{x_{3}^{q}}{t}}\biggr)^{q}-\unicode[STIX]{x1D6FE}_{1}{\displaystyle \frac{x_{3}^{q^{2}}}{t^{q}x_{2}^{q^{2}-1}}}\equiv \unicode[STIX]{x1D6FE}_{2}\biggl({\displaystyle \frac{x_{2}^{q}}{t}}+\biggl({\displaystyle \frac{x_{3}}{x_{1}}}\biggr)^{q}\biggr)\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right)\end{eqnarray}$$
$$\begin{eqnarray}\biggl(1+{\displaystyle \frac{x_{3}^{q}}{t}}\biggr)^{q}-\unicode[STIX]{x1D6FE}_{1}{\displaystyle \frac{x_{3}^{q^{2}}}{t^{q}x_{2}^{q^{2}-1}}}\equiv \unicode[STIX]{x1D6FE}_{2}\biggl({\displaystyle \frac{x_{2}^{q}}{t}}+\biggl({\displaystyle \frac{x_{3}}{x_{1}}}\biggr)^{q}\biggr)\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right)\end{eqnarray}$$
by (4.15), (4.18) and (4.20). We define a parameter
![]() $Z_{0}$
by
$Z_{0}$
by
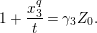 $$\begin{eqnarray}1+{\displaystyle \frac{x_{3}^{q}}{t}}=\unicode[STIX]{x1D6FE}_{3}Z_{0}.\end{eqnarray}$$
$$\begin{eqnarray}1+{\displaystyle \frac{x_{3}^{q}}{t}}=\unicode[STIX]{x1D6FE}_{3}Z_{0}.\end{eqnarray}$$
We note that
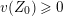 $v(Z_{0})\geqslant 0$
. Substituting this into (4.21), and dividing it by
$v(Z_{0})\geqslant 0$
. Substituting this into (4.21), and dividing it by
![]() $\unicode[STIX]{x1D6FE}_{2}$
, we obtain
$\unicode[STIX]{x1D6FE}_{2}$
, we obtain
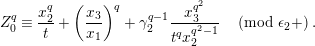 $$\begin{eqnarray}Z_{0}^{q}\equiv {\displaystyle \frac{x_{2}^{q}}{t}}+\biggl({\displaystyle \frac{x_{3}}{x_{1}}}\biggr)^{q}+\unicode[STIX]{x1D6FE}_{2}^{q-1}{\displaystyle \frac{x_{3}^{q^{2}}}{t^{q}x_{2}^{q^{2}-1}}}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right).\end{eqnarray}$$
$$\begin{eqnarray}Z_{0}^{q}\equiv {\displaystyle \frac{x_{2}^{q}}{t}}+\biggl({\displaystyle \frac{x_{3}}{x_{1}}}\biggr)^{q}+\unicode[STIX]{x1D6FE}_{2}^{q-1}{\displaystyle \frac{x_{3}^{q^{2}}}{t^{q}x_{2}^{q^{2}-1}}}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right).\end{eqnarray}$$
By (4.22) and (4.23), we acquire
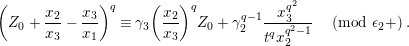 $$\begin{eqnarray}\biggl(Z_{0}+{\displaystyle \frac{x_{2}}{x_{3}}}-{\displaystyle \frac{x_{3}}{x_{1}}}\biggr)^{q}\equiv \unicode[STIX]{x1D6FE}_{3}\biggl({\displaystyle \frac{x_{2}}{x_{3}}}\biggr)^{q}Z_{0}+\unicode[STIX]{x1D6FE}_{2}^{q-1}{\displaystyle \frac{x_{3}^{q^{2}}}{t^{q}x_{2}^{q^{2}-1}}}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right).\end{eqnarray}$$
$$\begin{eqnarray}\biggl(Z_{0}+{\displaystyle \frac{x_{2}}{x_{3}}}-{\displaystyle \frac{x_{3}}{x_{1}}}\biggr)^{q}\equiv \unicode[STIX]{x1D6FE}_{3}\biggl({\displaystyle \frac{x_{2}}{x_{3}}}\biggr)^{q}Z_{0}+\unicode[STIX]{x1D6FE}_{2}^{q-1}{\displaystyle \frac{x_{3}^{q^{2}}}{t^{q}x_{2}^{q^{2}-1}}}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right).\end{eqnarray}$$
We introduce a new parameter
![]() $Z$
as
$Z$
as
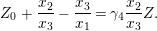 $$\begin{eqnarray}Z_{0}+{\displaystyle \frac{x_{2}}{x_{3}}}-{\displaystyle \frac{x_{3}}{x_{1}}}=\unicode[STIX]{x1D6FE}_{4}{\displaystyle \frac{x_{2}}{x_{3}}}Z.\end{eqnarray}$$
$$\begin{eqnarray}Z_{0}+{\displaystyle \frac{x_{2}}{x_{3}}}-{\displaystyle \frac{x_{3}}{x_{1}}}=\unicode[STIX]{x1D6FE}_{4}{\displaystyle \frac{x_{2}}{x_{3}}}Z.\end{eqnarray}$$
We note that
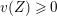 $v(Z)\geqslant 0$
. Substituting this into the left-hand side of the congruence (4.24), and dividing it by
$v(Z)\geqslant 0$
. Substituting this into the left-hand side of the congruence (4.24), and dividing it by
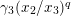 $\unicode[STIX]{x1D6FE}_{3}(x_{2}/x_{3})^{q}$
, we acquire
$\unicode[STIX]{x1D6FE}_{3}(x_{2}/x_{3})^{q}$
, we acquire
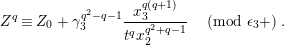 $$\begin{eqnarray}Z^{q}\equiv Z_{0}+\unicode[STIX]{x1D6FE}_{3}^{q^{2}-q-1}{\displaystyle \frac{x_{3}^{q(q+1)}}{t^{q}x_{2}^{q^{2}+q-1}}}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{3}+\right).\end{eqnarray}$$
$$\begin{eqnarray}Z^{q}\equiv Z_{0}+\unicode[STIX]{x1D6FE}_{3}^{q^{2}-q-1}{\displaystyle \frac{x_{3}^{q(q+1)}}{t^{q}x_{2}^{q^{2}+q-1}}}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{3}+\right).\end{eqnarray}$$
By substituting (4.25) into (4.26), we obtain
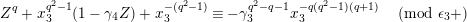 $$\begin{eqnarray}Z^{q}+x_{3}^{q^{2}-1}(1-\unicode[STIX]{x1D6FE}_{4}Z)+x_{3}^{-(q^{2}-1)}\equiv -\unicode[STIX]{x1D6FE}_{3}^{q^{2}-q-1}x_{3}^{-q(q^{2}-1)(q+1)}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{3}+\right)\end{eqnarray}$$
$$\begin{eqnarray}Z^{q}+x_{3}^{q^{2}-1}(1-\unicode[STIX]{x1D6FE}_{4}Z)+x_{3}^{-(q^{2}-1)}\equiv -\unicode[STIX]{x1D6FE}_{3}^{q^{2}-q-1}x_{3}^{-q(q^{2}-1)(q+1)}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{3}+\right)\end{eqnarray}$$
by (4.17), (4.20) and (4.22). Note that we have
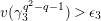 $v(\unicode[STIX]{x1D6FE}_{3}^{q^{2}-q-1})>\unicode[STIX]{x1D716}_{3}$
, if
$v(\unicode[STIX]{x1D6FE}_{3}^{q^{2}-q-1})>\unicode[STIX]{x1D716}_{3}$
, if
![]() $q\neq 2$
.
$q\neq 2$
.
Proposition 4.4. The reduction of the space
![]() $\mathbf{Z}_{1,1}^{0}$
is isomorphic to the affine curve defined by
$\mathbf{Z}_{1,1}^{0}$
is isomorphic to the affine curve defined by
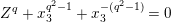 $Z^{q}+x_{3}^{q^{2}-1}+x_{3}^{-(q^{2}-1)}=0$
. This affine curve has genus
$Z^{q}+x_{3}^{q^{2}-1}+x_{3}^{-(q^{2}-1)}=0$
. This affine curve has genus
![]() $0$
and singularities at
$0$
and singularities at
![]() $x_{3}\in {\mathcal{S}}_{1}$
.
$x_{3}\in {\mathcal{S}}_{1}$
.
Proof. The required assertion follows from the congruence (4.27) modulo
![]() $0+$
.◻
$0+$
.◻
Definition 4.5.
-
(1) For any
 $\unicode[STIX]{x1D701}\in {\mathcal{S}}_{1}$
, we define a subspace by
$\unicode[STIX]{x1D701}\in {\mathcal{S}}_{1}$
, we define a subspace by $$\begin{eqnarray}{\mathcal{D}}_{\unicode[STIX]{x1D701}}\subset \mathbf{Z}_{1,1}^{0}\times _{\widehat{K}^{\text{ur}}}\widehat{K}^{\text{ur}}(\unicode[STIX]{x1D714}_{3})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{D}}_{\unicode[STIX]{x1D701}}\subset \mathbf{Z}_{1,1}^{0}\times _{\widehat{K}^{\text{ur}}}\widehat{K}^{\text{ur}}(\unicode[STIX]{x1D714}_{3})\end{eqnarray}$$
 $\bar{x}_{3}=\unicode[STIX]{x1D701}$
. We call the space
$\bar{x}_{3}=\unicode[STIX]{x1D701}$
. We call the space
 ${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
a singular residue class of
${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
a singular residue class of
 $\mathbf{Z}_{1,1}^{0}$
.
$\mathbf{Z}_{1,1}^{0}$
.
-
(2) We define a subspace
by the complement $$\begin{eqnarray}\mathbf{Z}_{1,1}\subset \mathbf{Z}_{1,1}^{0}\times _{\widehat{K}^{\text{ur}}}\widehat{K}^{\text{ur}}(\unicode[STIX]{x1D714}_{3})\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{Z}_{1,1}\subset \mathbf{Z}_{1,1}^{0}\times _{\widehat{K}^{\text{ur}}}\widehat{K}^{\text{ur}}(\unicode[STIX]{x1D714}_{3})\end{eqnarray}$$
 $\mathbf{Z}_{1,1}^{0}\times _{\widehat{K}^{\text{ur}}}\widehat{K}^{\text{ur}}(\unicode[STIX]{x1D714}_{3})\backslash \bigcup _{\unicode[STIX]{x1D701}\in {\mathcal{S}}_{1}}{\mathcal{D}}_{\unicode[STIX]{x1D701}}$
.
$\mathbf{Z}_{1,1}^{0}\times _{\widehat{K}^{\text{ur}}}\widehat{K}^{\text{ur}}(\unicode[STIX]{x1D714}_{3})\backslash \bigcup _{\unicode[STIX]{x1D701}\in {\mathcal{S}}_{1}}{\mathcal{D}}_{\unicode[STIX]{x1D701}}$
.
Proposition 4.6. The reduction of the space
![]() $\mathbf{Z}_{1,1}$
is isomorphic to the affine curve defined by
$\mathbf{Z}_{1,1}$
is isomorphic to the affine curve defined by
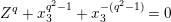 $Z^{q}+x_{3}^{q^{2}-1}+x_{3}^{-(q^{2}-1)}=0$
with
$Z^{q}+x_{3}^{q^{2}-1}+x_{3}^{-(q^{2}-1)}=0$
with
![]() $x_{3}\notin {\mathcal{S}}_{1}$
.
$x_{3}\notin {\mathcal{S}}_{1}$
.
Proof. This follows from Proposition 4.4. ◻
4.4 Analysis of the singular residue classes of
 $\mathbf{Z}_{1,1}^{0}$
$\mathbf{Z}_{1,1}^{0}$
In this subsection, we analyze the singular residue classes
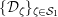 $\{{\mathcal{D}}_{\unicode[STIX]{x1D701}}\}_{\unicode[STIX]{x1D701}\in {\mathcal{S}}_{1}}$
of
$\{{\mathcal{D}}_{\unicode[STIX]{x1D701}}\}_{\unicode[STIX]{x1D701}\in {\mathcal{S}}_{1}}$
of
![]() $\mathbf{Z}_{1,1}^{0}$
. If
$\mathbf{Z}_{1,1}^{0}$
. If
![]() $q$
is odd, the space
$q$
is odd, the space
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
is a basic wide open space with an underlying affinoid
${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
is a basic wide open space with an underlying affinoid
![]() $\mathbf{X}_{\unicode[STIX]{x1D701}}$
, whose reduction
$\mathbf{X}_{\unicode[STIX]{x1D701}}$
, whose reduction
![]() $\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}$
is isomorphic to the affine curve defined by
$\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}$
is isomorphic to the affine curve defined by
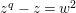 $z^{q}-z=w^{2}$
. On the other hand, if
$z^{q}-z=w^{2}$
. On the other hand, if
![]() $q$
is even, the situation is slightly complicated, because the space
$q$
is even, the situation is slightly complicated, because the space
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
is not basic wide open. Hence, we have to cover
${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
is not basic wide open. Hence, we have to cover
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
by smaller basic wide open spaces. As a result, in
${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
by smaller basic wide open spaces. As a result, in
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
, we find an affinoid
${\mathcal{D}}_{\unicode[STIX]{x1D701}}$
, we find an affinoid
![]() $\mathbf{P}_{\unicode[STIX]{x1D701}}^{0}$
, whose reduction is isomorphic to the affine curve defined by
$\mathbf{P}_{\unicode[STIX]{x1D701}}^{0}$
, whose reduction is isomorphic to the affine curve defined by
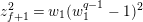 $z_{f+1}^{2}=w_{1}(w_{1}^{q-1}-1)^{2}$
. This affine curve has
$z_{f+1}^{2}=w_{1}(w_{1}^{q-1}-1)^{2}$
. This affine curve has
![]() $q-1$
singular points at
$q-1$
singular points at
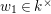 $w_{1}\in k^{\times }$
. Then, by analyzing the tubular neighborhoods of these singular points, we find an affinoid
$w_{1}\in k^{\times }$
. Then, by analyzing the tubular neighborhoods of these singular points, we find an affinoid
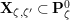 $\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}\subset \mathbf{P}_{\unicode[STIX]{x1D701}}^{0}$
for each
$\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}\subset \mathbf{P}_{\unicode[STIX]{x1D701}}^{0}$
for each
![]() $\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
, whose reduction is isomorphic to the affine curve defined by
$\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
, whose reduction is isomorphic to the affine curve defined by
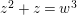 $z^{2}+z=w^{3}$
.
$z^{2}+z=w^{3}$
.
4.4.1
 $q$
odd
$q$
odd
We assume that
![]() $q$
is odd. For each
$q$
is odd. For each
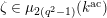 $\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})$
, we define an affinoid
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})$
, we define an affinoid
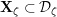 $\mathbf{X}_{\unicode[STIX]{x1D701}}\subset {\mathcal{D}}_{\unicode[STIX]{x1D701}}$
and compute its reduction
$\mathbf{X}_{\unicode[STIX]{x1D701}}\subset {\mathcal{D}}_{\unicode[STIX]{x1D701}}$
and compute its reduction
![]() $\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}$
.
$\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}$
.
For
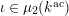 $\unicode[STIX]{x1D704}\in \unicode[STIX]{x1D707}_{2}(k^{\text{ac}})$
, we choose an element
$\unicode[STIX]{x1D704}\in \unicode[STIX]{x1D707}_{2}(k^{\text{ac}})$
, we choose an element
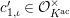 $c_{1,\unicode[STIX]{x1D704}}^{\prime }\in {\mathcal{O}}_{K^{\text{ac}}}^{\times }$
such that
$c_{1,\unicode[STIX]{x1D704}}^{\prime }\in {\mathcal{O}}_{K^{\text{ac}}}^{\times }$
such that
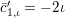 $\bar{c}_{1,\unicode[STIX]{x1D704}}^{\prime }=-2\unicode[STIX]{x1D704}$
and
$\bar{c}_{1,\unicode[STIX]{x1D704}}^{\prime }=-2\unicode[STIX]{x1D704}$
and
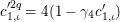 $c_{1,\unicode[STIX]{x1D704}}^{\prime 2q}=4(1-\unicode[STIX]{x1D6FE}_{4}c_{1,\unicode[STIX]{x1D704}}^{\prime })$
. We take
$c_{1,\unicode[STIX]{x1D704}}^{\prime 2q}=4(1-\unicode[STIX]{x1D6FE}_{4}c_{1,\unicode[STIX]{x1D704}}^{\prime })$
. We take
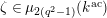 $\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})$
. We put
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})$
. We put
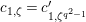 $c_{1,\unicode[STIX]{x1D701}}=c_{1,\unicode[STIX]{x1D701}^{q^{2}-1}}^{\prime }$
, and define
$c_{1,\unicode[STIX]{x1D701}}=c_{1,\unicode[STIX]{x1D701}^{q^{2}-1}}^{\prime }$
, and define
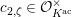 $c_{2,\unicode[STIX]{x1D701}}\in {\mathcal{O}}_{K^{\text{ac}}}^{\times }$
by
$c_{2,\unicode[STIX]{x1D701}}\in {\mathcal{O}}_{K^{\text{ac}}}^{\times }$
by
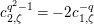 $c_{2,\unicode[STIX]{x1D701}}^{q^{2}-1}=-2c_{1,\unicode[STIX]{x1D701}}^{-q}$
and
$c_{2,\unicode[STIX]{x1D701}}^{q^{2}-1}=-2c_{1,\unicode[STIX]{x1D701}}^{-q}$
and
![]() $\bar{c}_{2,\unicode[STIX]{x1D701}}=\unicode[STIX]{x1D701}$
. We put
$\bar{c}_{2,\unicode[STIX]{x1D701}}=\unicode[STIX]{x1D701}$
. We put
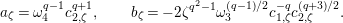 $$\begin{eqnarray}a_{\unicode[STIX]{x1D701}}=\unicode[STIX]{x1D714}_{4}^{q-1}c_{2,\unicode[STIX]{x1D701}}^{q+1},\qquad b_{\unicode[STIX]{x1D701}}=-2\unicode[STIX]{x1D701}^{q^{2}-1}\unicode[STIX]{x1D714}_{3}^{(q-1)/2}c_{1,\unicode[STIX]{x1D701}}^{-q}c_{2,\unicode[STIX]{x1D701}}^{(q+3)/2}.\end{eqnarray}$$
$$\begin{eqnarray}a_{\unicode[STIX]{x1D701}}=\unicode[STIX]{x1D714}_{4}^{q-1}c_{2,\unicode[STIX]{x1D701}}^{q+1},\qquad b_{\unicode[STIX]{x1D701}}=-2\unicode[STIX]{x1D701}^{q^{2}-1}\unicode[STIX]{x1D714}_{3}^{(q-1)/2}c_{1,\unicode[STIX]{x1D701}}^{-q}c_{2,\unicode[STIX]{x1D701}}^{(q+3)/2}.\end{eqnarray}$$
Note that we have
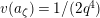 $v(a_{\unicode[STIX]{x1D701}})=1/(2q^{4})$
and
$v(a_{\unicode[STIX]{x1D701}})=1/(2q^{4})$
and
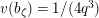 $v(b_{\unicode[STIX]{x1D701}})=1/(4q^{3})$
.
$v(b_{\unicode[STIX]{x1D701}})=1/(4q^{3})$
.
For an element
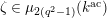 $\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})$
, we define an affinoid
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})$
, we define an affinoid
![]() $\mathbf{X}_{\unicode[STIX]{x1D701}}$
by
$\mathbf{X}_{\unicode[STIX]{x1D701}}$
by
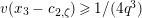 $v(x_{3}-c_{2,\unicode[STIX]{x1D701}})\geqslant 1/(4q^{3})$
. We change variables as
$v(x_{3}-c_{2,\unicode[STIX]{x1D701}})\geqslant 1/(4q^{3})$
. We change variables as
 $$\begin{eqnarray}Z=a_{\unicode[STIX]{x1D701}}z+c_{1,\unicode[STIX]{x1D701}},\qquad x_{3}=b_{\unicode[STIX]{x1D701}}w+c_{2,\unicode[STIX]{x1D701}}.\end{eqnarray}$$
$$\begin{eqnarray}Z=a_{\unicode[STIX]{x1D701}}z+c_{1,\unicode[STIX]{x1D701}},\qquad x_{3}=b_{\unicode[STIX]{x1D701}}w+c_{2,\unicode[STIX]{x1D701}}.\end{eqnarray}$$
Then, we acquire
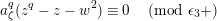 $$\begin{eqnarray}a_{\unicode[STIX]{x1D701}}^{q}(z^{q}-z-w^{2})\equiv 0\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{3}+\right)\end{eqnarray}$$
$$\begin{eqnarray}a_{\unicode[STIX]{x1D701}}^{q}(z^{q}-z-w^{2})\equiv 0\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{3}+\right)\end{eqnarray}$$
by (4.27). Dividing this by
![]() $a_{\unicode[STIX]{x1D701}}^{q}$
, we have
$a_{\unicode[STIX]{x1D701}}^{q}$
, we have
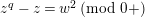 $z^{q}-z=w^{2}\;(\text{mod}~0+)$
. Hence, the reduction of
$z^{q}-z=w^{2}\;(\text{mod}~0+)$
. Hence, the reduction of
![]() $\mathbf{X}_{\unicode[STIX]{x1D701}}$
is isomorphic to the affine curve defined by
$\mathbf{X}_{\unicode[STIX]{x1D701}}$
is isomorphic to the affine curve defined by
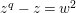 $z^{q}-z=w^{2}$
.
$z^{q}-z=w^{2}$
.
Proposition 4.7. For each
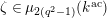 $\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})$
, the reduction
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})$
, the reduction
![]() $\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}$
is isomorphic to the affine curve defined by
$\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}$
is isomorphic to the affine curve defined by
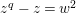 $z^{q}-z=w^{2}$
, and the complement
$z^{q}-z=w^{2}$
, and the complement
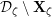 ${\mathcal{D}}_{\unicode[STIX]{x1D701}}\setminus \mathbf{X}_{\unicode[STIX]{x1D701}}$
is an open annulus.
${\mathcal{D}}_{\unicode[STIX]{x1D701}}\setminus \mathbf{X}_{\unicode[STIX]{x1D701}}$
is an open annulus.
Proof. We have already proved the first assertion. We prove the second assertion. We change variables as
 $$\begin{eqnarray}Z=z^{\prime }+c_{1,\unicode[STIX]{x1D701}},\qquad x_{3}=w^{\prime }+c_{2,\unicode[STIX]{x1D701}}\end{eqnarray}$$
$$\begin{eqnarray}Z=z^{\prime }+c_{1,\unicode[STIX]{x1D701}},\qquad x_{3}=w^{\prime }+c_{2,\unicode[STIX]{x1D701}}\end{eqnarray}$$
with
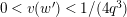 $0<v(w^{\prime })<1/(4q^{3})$
. Substituting them into (4.27), we obtain
$0<v(w^{\prime })<1/(4q^{3})$
. Substituting them into (4.27), we obtain
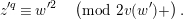 $$\begin{eqnarray}z^{\prime q}\equiv w^{\prime 2}\quad \left(\text{mod}~2v(w^{\prime })+\right).\end{eqnarray}$$
$$\begin{eqnarray}z^{\prime q}\equiv w^{\prime 2}\quad \left(\text{mod}~2v(w^{\prime })+\right).\end{eqnarray}$$
Note that we have
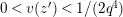 $0<v(z^{\prime })<1/(2q^{4})$
. By setting
$0<v(z^{\prime })<1/(2q^{4})$
. By setting
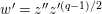 $w^{\prime }=z^{\prime \prime }z^{\prime (q-1)/2}$
, we acquire
$w^{\prime }=z^{\prime \prime }z^{\prime (q-1)/2}$
, we acquire
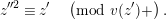 $$\begin{eqnarray}z^{\prime \prime 2}\equiv z^{\prime }\quad \left(\text{mod}~v(z^{\prime })+\right).\end{eqnarray}$$
$$\begin{eqnarray}z^{\prime \prime 2}\equiv z^{\prime }\quad \left(\text{mod}~v(z^{\prime })+\right).\end{eqnarray}$$
Hence, we can see that
![]() $z^{\prime }$
is written as a function of
$z^{\prime }$
is written as a function of
![]() $z^{\prime \prime }$
. Then,
$z^{\prime \prime }$
. Then,
![]() $w^{\prime }$
is also written as a function of
$w^{\prime }$
is also written as a function of
![]() $z^{\prime \prime }$
. Therefore,
$z^{\prime \prime }$
. Therefore,
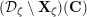 $({\mathcal{D}}_{\unicode[STIX]{x1D701}}\setminus \mathbf{X}_{\unicode[STIX]{x1D701}})(\mathbf{C})$
is identified with
$({\mathcal{D}}_{\unicode[STIX]{x1D701}}\setminus \mathbf{X}_{\unicode[STIX]{x1D701}})(\mathbf{C})$
is identified with
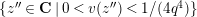 $\{z^{\prime \prime }\in \mathbf{C}\mid 0<v(z^{\prime \prime })<1/(4q^{4})\}$
.◻
$\{z^{\prime \prime }\in \mathbf{C}\mid 0<v(z^{\prime \prime })<1/(4q^{4})\}$
.◻
4.4.2
 $q$
even
$q$
even
We assume that
![]() $q$
is even. We put
$q$
is even. We put
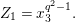 $$\begin{eqnarray}Z_{1}=x_{3}^{q^{2}-1}.\end{eqnarray}$$
$$\begin{eqnarray}Z_{1}=x_{3}^{q^{2}-1}.\end{eqnarray}$$
Then, the congruence (4.27) has the following form:
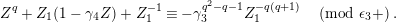 $$\begin{eqnarray}Z^{q}+Z_{1}(1-\unicode[STIX]{x1D6FE}_{4}Z)+Z_{1}^{-1}\equiv -\unicode[STIX]{x1D6FE}_{3}^{q^{2}-q-1}Z_{1}^{-q(q+1)}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{3}+\right).\end{eqnarray}$$
$$\begin{eqnarray}Z^{q}+Z_{1}(1-\unicode[STIX]{x1D6FE}_{4}Z)+Z_{1}^{-1}\equiv -\unicode[STIX]{x1D6FE}_{3}^{q^{2}-q-1}Z_{1}^{-q(q+1)}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{3}+\right).\end{eqnarray}$$
1. Projective lines For each
![]() $\unicode[STIX]{x1D701}\in k_{2}^{\times }$
, we define a subaffinoid
$\unicode[STIX]{x1D701}\in k_{2}^{\times }$
, we define a subaffinoid
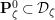 $\mathbf{P}_{\unicode[STIX]{x1D701}}^{0}\subset {\mathcal{D}}_{\unicode[STIX]{x1D701}}$
by
$\mathbf{P}_{\unicode[STIX]{x1D701}}^{0}\subset {\mathcal{D}}_{\unicode[STIX]{x1D701}}$
by
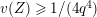 $v(Z)\geqslant 1/(4q^{4})$
. We change variables as
$v(Z)\geqslant 1/(4q^{4})$
. We change variables as
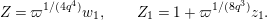 $$\begin{eqnarray}Z=\unicode[STIX]{x1D71B}^{1/(4q^{4})}w_{1},\qquad Z_{1}=1+\unicode[STIX]{x1D71B}^{1/(8q^{3})}z_{1}.\end{eqnarray}$$
$$\begin{eqnarray}Z=\unicode[STIX]{x1D71B}^{1/(4q^{4})}w_{1},\qquad Z_{1}=1+\unicode[STIX]{x1D71B}^{1/(8q^{3})}z_{1}.\end{eqnarray}$$
Substituting these into (4.28) and dividing it by
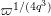 $\unicode[STIX]{x1D71B}^{1/(4q^{3})}$
, we acquire
$\unicode[STIX]{x1D71B}^{1/(4q^{3})}$
, we acquire
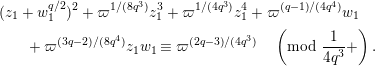 $$\begin{eqnarray}\displaystyle & & \displaystyle \quad (z_{1}+w_{1}^{q/2})^{2}+\unicode[STIX]{x1D71B}^{1/(8q^{3})}z_{1}^{3}+\unicode[STIX]{x1D71B}^{1/(4q^{3})}z_{1}^{4}+\unicode[STIX]{x1D71B}^{(q-1)/(4q^{4})}w_{1}\nonumber\\ \displaystyle & & \displaystyle \quad \qquad +\,\unicode[STIX]{x1D71B}^{(3q-2)/(8q^{4})}z_{1}w_{1}\equiv \unicode[STIX]{x1D71B}^{(2q-3)/(4q^{3})}\quad \left(\text{mod}~{\displaystyle \frac{1}{4q^{3}}}+\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \quad (z_{1}+w_{1}^{q/2})^{2}+\unicode[STIX]{x1D71B}^{1/(8q^{3})}z_{1}^{3}+\unicode[STIX]{x1D71B}^{1/(4q^{3})}z_{1}^{4}+\unicode[STIX]{x1D71B}^{(q-1)/(4q^{4})}w_{1}\nonumber\\ \displaystyle & & \displaystyle \quad \qquad +\,\unicode[STIX]{x1D71B}^{(3q-2)/(8q^{4})}z_{1}w_{1}\equiv \unicode[STIX]{x1D71B}^{(2q-3)/(4q^{3})}\quad \left(\text{mod}~{\displaystyle \frac{1}{4q^{3}}}+\right).\end{eqnarray}$$
We can check that
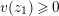 $v(z_{1})\geqslant 0$
. We set
$v(z_{1})\geqslant 0$
. We set
![]() $q=2^{f}$
and put
$q=2^{f}$
and put
 $$\begin{eqnarray}l_{i}={\displaystyle \frac{(2^{i}-1)q}{2^{i}}},\qquad m_{i}={\displaystyle \frac{1}{2^{i+2}q^{3}}}\end{eqnarray}$$
$$\begin{eqnarray}l_{i}={\displaystyle \frac{(2^{i}-1)q}{2^{i}}},\qquad m_{i}={\displaystyle \frac{1}{2^{i+2}q^{3}}}\end{eqnarray}$$
for
 $1\leqslant i\leqslant f+1$
. Furthermore, we define parameters
$1\leqslant i\leqslant f+1$
. Furthermore, we define parameters
![]() $z_{i}$
for
$z_{i}$
for
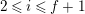 $2\leqslant i\leqslant f+1$
by
$2\leqslant i\leqslant f+1$
by
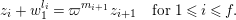 $$\begin{eqnarray}z_{i}+w_{1}^{l_{i}}=\unicode[STIX]{x1D71B}^{m_{i+1}}z_{i+1}\quad \text{for }1\leqslant i\leqslant f.\end{eqnarray}$$
$$\begin{eqnarray}z_{i}+w_{1}^{l_{i}}=\unicode[STIX]{x1D71B}^{m_{i+1}}z_{i+1}\quad \text{for }1\leqslant i\leqslant f.\end{eqnarray}$$
Lemma 4.8. We assume that
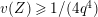 $v(Z)\geqslant 1/(4q^{4})$
. Then, we have
$v(Z)\geqslant 1/(4q^{4})$
. Then, we have
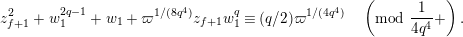 $$\begin{eqnarray}\displaystyle z_{f+1}^{2}+w_{1}^{2q-1}+w_{1}+\unicode[STIX]{x1D71B}^{1/(8q^{4})}z_{f+1}w_{1}^{q}\equiv (q/2)\unicode[STIX]{x1D71B}^{1/(4q^{4})}\quad \left(\text{mod}~{\displaystyle \frac{1}{4q^{4}}}+\right). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle z_{f+1}^{2}+w_{1}^{2q-1}+w_{1}+\unicode[STIX]{x1D71B}^{1/(8q^{4})}z_{f+1}w_{1}^{q}\equiv (q/2)\unicode[STIX]{x1D71B}^{1/(4q^{4})}\quad \left(\text{mod}~{\displaystyle \frac{1}{4q^{4}}}+\right). & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Proof. If
![]() $q=2$
, we can check that
$q=2$
, we can check that
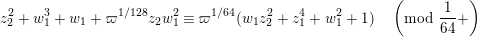 $$\begin{eqnarray}\displaystyle z_{2}^{2}+w_{1}^{3}+w_{1}+\unicode[STIX]{x1D71B}^{1/128}z_{2}w_{1}^{2}\equiv \unicode[STIX]{x1D71B}^{1/64}(w_{1}z_{2}^{2}+z_{1}^{4}+w_{1}^{2}+1)\quad \left(\text{mod}~{\displaystyle \frac{1}{64}}+\right) & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle z_{2}^{2}+w_{1}^{3}+w_{1}+\unicode[STIX]{x1D71B}^{1/128}z_{2}w_{1}^{2}\equiv \unicode[STIX]{x1D71B}^{1/64}(w_{1}z_{2}^{2}+z_{1}^{4}+w_{1}^{2}+1)\quad \left(\text{mod}~{\displaystyle \frac{1}{64}}+\right) & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
by
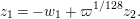 $$\begin{eqnarray}z_{1}=-w_{1}+\unicode[STIX]{x1D71B}^{1/128}z_{2}.\end{eqnarray}$$
$$\begin{eqnarray}z_{1}=-w_{1}+\unicode[STIX]{x1D71B}^{1/128}z_{2}.\end{eqnarray}$$
We have
 $v(z_{2}^{2}+w_{1}^{3}+w_{1})>0$
. Therefore, we obtain
$v(z_{2}^{2}+w_{1}^{3}+w_{1})>0$
. Therefore, we obtain
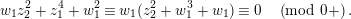 $$\begin{eqnarray}w_{1}z_{2}^{2}+z_{1}^{4}+w_{1}^{2}\equiv w_{1}(z_{2}^{2}+w_{1}^{3}+w_{1})\equiv 0\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
$$\begin{eqnarray}w_{1}z_{2}^{2}+z_{1}^{4}+w_{1}^{2}\equiv w_{1}(z_{2}^{2}+w_{1}^{3}+w_{1})\equiv 0\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
Hence, the required assertion in this case follows from (4.32). Assume that
![]() $f\geqslant 2$
. For
$f\geqslant 2$
. For
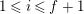 $1\leqslant i\leqslant f+1$
, we put
$1\leqslant i\leqslant f+1$
, we put
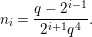 $$\begin{eqnarray}n_{i}={\displaystyle \frac{q-2^{i-1}}{2^{i+1}q^{4}}}.\end{eqnarray}$$
$$\begin{eqnarray}n_{i}={\displaystyle \frac{q-2^{i-1}}{2^{i+1}q^{4}}}.\end{eqnarray}$$
We prove
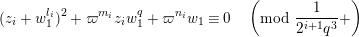 $$\begin{eqnarray}(z_{i}+w_{1}^{l_{i}})^{2}+\unicode[STIX]{x1D71B}^{m_{i}}z_{i}w_{1}^{q}+\unicode[STIX]{x1D71B}^{n_{i}}w_{1}\equiv 0\quad \left(\text{mod}~{\displaystyle \frac{1}{2^{i+1}q^{3}}}+\right)\end{eqnarray}$$
$$\begin{eqnarray}(z_{i}+w_{1}^{l_{i}})^{2}+\unicode[STIX]{x1D71B}^{m_{i}}z_{i}w_{1}^{q}+\unicode[STIX]{x1D71B}^{n_{i}}w_{1}\equiv 0\quad \left(\text{mod}~{\displaystyle \frac{1}{2^{i+1}q^{3}}}+\right)\end{eqnarray}$$
for
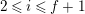 $2\leqslant i\leqslant f+1$
by induction on
$2\leqslant i\leqslant f+1$
by induction on
![]() $i$
. Eliminating
$i$
. Eliminating
![]() $z_{1}$
from (4.29) by (4.30) and dividing it by
$z_{1}$
from (4.29) by (4.30) and dividing it by
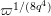 $\unicode[STIX]{x1D71B}^{1/(8q^{4})}$
, we obtain
$\unicode[STIX]{x1D71B}^{1/(8q^{4})}$
, we obtain
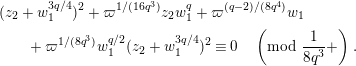 $$\begin{eqnarray}\displaystyle & & \displaystyle (z_{2}+w_{1}^{3q/4})^{2}+\unicode[STIX]{x1D71B}^{1/(16q^{3})}z_{2}w_{1}^{q}+\unicode[STIX]{x1D71B}^{(q-2)/(8q^{4})}w_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D71B}^{1/(8q^{3})}w_{1}^{q/2}(z_{2}+w_{1}^{3q/4})^{2}\equiv 0\quad \left(\text{mod}~{\displaystyle \frac{1}{8q^{3}}}+\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (z_{2}+w_{1}^{3q/4})^{2}+\unicode[STIX]{x1D71B}^{1/(16q^{3})}z_{2}w_{1}^{q}+\unicode[STIX]{x1D71B}^{(q-2)/(8q^{4})}w_{1}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D71B}^{1/(8q^{3})}w_{1}^{q/2}(z_{2}+w_{1}^{3q/4})^{2}\equiv 0\quad \left(\text{mod}~{\displaystyle \frac{1}{8q^{3}}}+\right).\nonumber\end{eqnarray}$$
This shows
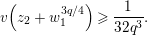 $$\begin{eqnarray}v\Bigl(z_{2}+w_{1}^{3q/4}\Bigr)\geqslant {\displaystyle \frac{1}{32q^{3}}}.\end{eqnarray}$$
$$\begin{eqnarray}v\Bigl(z_{2}+w_{1}^{3q/4}\Bigr)\geqslant {\displaystyle \frac{1}{32q^{3}}}.\end{eqnarray}$$
Hence, we have (4.33) for
![]() $i=2$
. Assume (4.33) for
$i=2$
. Assume (4.33) for
![]() $i$
. Eliminating
$i$
. Eliminating
![]() $z_{i}$
from (4.33) by (4.30) and dividing it by
$z_{i}$
from (4.33) by (4.30) and dividing it by
![]() $\unicode[STIX]{x1D71B}^{m_{i}}$
, we obtain (4.33) for
$\unicode[STIX]{x1D71B}^{m_{i}}$
, we obtain (4.33) for
![]() $i+1$
. Hence, we have (4.33) for
$i+1$
. Hence, we have (4.33) for
![]() $f+1$
, which is equivalent to (4.31).◻
$f+1$
, which is equivalent to (4.31).◻
Proposition 4.9. For each
![]() $\unicode[STIX]{x1D701}\in k_{2}^{\times }$
, the reduction
$\unicode[STIX]{x1D701}\in k_{2}^{\times }$
, the reduction
![]() $\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}^{0}$
is isomorphic to the affine curve defined by
$\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}^{0}$
is isomorphic to the affine curve defined by
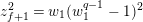 $z_{f+1}^{2}=w_{1}(w_{1}^{q-1}-1)^{2}$
, which has genus
$z_{f+1}^{2}=w_{1}(w_{1}^{q-1}-1)^{2}$
, which has genus
![]() $0$
and singularities at
$0$
and singularities at
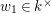 $w_{1}\in k^{\times }$
, and the complement
$w_{1}\in k^{\times }$
, and the complement
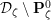 ${\mathcal{D}}_{\unicode[STIX]{x1D701}}\setminus \mathbf{P}_{\unicode[STIX]{x1D701}}^{0}$
is an open annulus.
${\mathcal{D}}_{\unicode[STIX]{x1D701}}\setminus \mathbf{P}_{\unicode[STIX]{x1D701}}^{0}$
is an open annulus.
Proof. The claim on
![]() $\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}^{0}$
follows from the congruence (4.31) modulo
$\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}^{0}$
follows from the congruence (4.31) modulo
![]() $0+$
. We prove the last assertion. We change a variable as
$0+$
. We prove the last assertion. We change a variable as
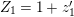 $Z_{1}=1+z_{1}^{\prime }$
with
$Z_{1}=1+z_{1}^{\prime }$
with
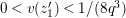 $0<v(z_{1}^{\prime })<1/(8q^{3})$
. Similarly to (4.30), we introduce parameters
$0<v(z_{1}^{\prime })<1/(8q^{3})$
. Similarly to (4.30), we introduce parameters
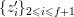 $\{z_{i}^{\prime }\}_{2\leqslant i\leqslant f+1}$
by
$\{z_{i}^{\prime }\}_{2\leqslant i\leqslant f+1}$
by
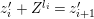 $z_{i}^{\prime }+Z^{l_{i}}=z_{i+1}^{\prime }$
for
$z_{i}^{\prime }+Z^{l_{i}}=z_{i+1}^{\prime }$
for
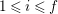 $1\leqslant i\leqslant f$
. Then, by similar computations to those in the proof of Lemma 4.8, we obtain
$1\leqslant i\leqslant f$
. Then, by similar computations to those in the proof of Lemma 4.8, we obtain
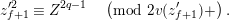 $$\begin{eqnarray}z_{f+1}^{\prime 2}\equiv Z^{2q-1}\quad \left(\text{mod}~2v(z_{f+1}^{\prime })+\right).\end{eqnarray}$$
$$\begin{eqnarray}z_{f+1}^{\prime 2}\equiv Z^{2q-1}\quad \left(\text{mod}~2v(z_{f+1}^{\prime })+\right).\end{eqnarray}$$
By setting
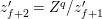 $z_{f+2}^{\prime }=Z^{q}/z_{f+1}^{\prime }$
, we obtain
$z_{f+2}^{\prime }=Z^{q}/z_{f+1}^{\prime }$
, we obtain
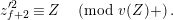 $$\begin{eqnarray}z_{f+2}^{\prime 2}\equiv Z\quad \left(\text{mod}~v(Z)+\right).\end{eqnarray}$$
$$\begin{eqnarray}z_{f+2}^{\prime 2}\equiv Z\quad \left(\text{mod}~v(Z)+\right).\end{eqnarray}$$
Then, we can see that all parameters
![]() $z_{i}^{\prime }$
for
$z_{i}^{\prime }$
for
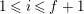 $1\leqslant i\leqslant f+1$
and
$1\leqslant i\leqslant f+1$
and
![]() $Z$
are written as functions of
$Z$
are written as functions of
![]() $z_{f+2}^{\prime }$
. Hence,
$z_{f+2}^{\prime }$
. Hence,
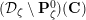 $({\mathcal{D}}_{\unicode[STIX]{x1D701}}\setminus \mathbf{P}_{\unicode[STIX]{x1D701}}^{0})(\mathbf{C})$
is identified with
$({\mathcal{D}}_{\unicode[STIX]{x1D701}}\setminus \mathbf{P}_{\unicode[STIX]{x1D701}}^{0})(\mathbf{C})$
is identified with
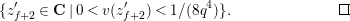 $$\begin{eqnarray}\{z_{f+2}^{\prime }\in \mathbf{C}\mid 0<v(z_{f+2}^{\prime })<1/(8q^{4})\}.\square\end{eqnarray}$$
$$\begin{eqnarray}\{z_{f+2}^{\prime }\in \mathbf{C}\mid 0<v(z_{f+2}^{\prime })<1/(8q^{4})\}.\square\end{eqnarray}$$
2. Elliptic curves For
![]() $\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
, we choose
$\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
, we choose
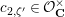 $c_{2,\unicode[STIX]{x1D701}^{\prime }}\in {\mathcal{O}}_{\mathbf{C}}^{\times }$
such that
$c_{2,\unicode[STIX]{x1D701}^{\prime }}\in {\mathcal{O}}_{\mathbf{C}}^{\times }$
such that
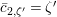 $\bar{c}_{2,\unicode[STIX]{x1D701}^{\prime }}=\unicode[STIX]{x1D701}^{\prime }$
and
$\bar{c}_{2,\unicode[STIX]{x1D701}^{\prime }}=\unicode[STIX]{x1D701}^{\prime }$
and
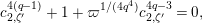 $$\begin{eqnarray}c_{2,\unicode[STIX]{x1D701}^{\prime }}^{4(q-1)}+1+\unicode[STIX]{x1D71B}^{1/(4q^{4})}c_{2,\unicode[STIX]{x1D701}^{\prime }}^{4q-3}=0,\end{eqnarray}$$
$$\begin{eqnarray}c_{2,\unicode[STIX]{x1D701}^{\prime }}^{4(q-1)}+1+\unicode[STIX]{x1D71B}^{1/(4q^{4})}c_{2,\unicode[STIX]{x1D701}^{\prime }}^{4q-3}=0,\end{eqnarray}$$
and a square root
![]() $c_{2,\unicode[STIX]{x1D701}^{\prime }}^{1/2}$
of
$c_{2,\unicode[STIX]{x1D701}^{\prime }}^{1/2}$
of
![]() $c_{2,\unicode[STIX]{x1D701}^{\prime }}$
. Further, we choose
$c_{2,\unicode[STIX]{x1D701}^{\prime }}$
. Further, we choose
![]() $c_{1,\unicode[STIX]{x1D701}^{\prime }}$
such that
$c_{1,\unicode[STIX]{x1D701}^{\prime }}$
such that
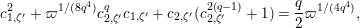 $$\begin{eqnarray}c_{1,\unicode[STIX]{x1D701}^{\prime }}^{2}+\unicode[STIX]{x1D71B}^{1/(8q^{4})}c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q}c_{1,\unicode[STIX]{x1D701}^{\prime }}+c_{2,\unicode[STIX]{x1D701}^{\prime }}(c_{2,\unicode[STIX]{x1D701}^{\prime }}^{2(q-1)}+1)={\displaystyle \frac{q}{2}}\unicode[STIX]{x1D71B}^{1/(4q^{4})},\end{eqnarray}$$
$$\begin{eqnarray}c_{1,\unicode[STIX]{x1D701}^{\prime }}^{2}+\unicode[STIX]{x1D71B}^{1/(8q^{4})}c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q}c_{1,\unicode[STIX]{x1D701}^{\prime }}+c_{2,\unicode[STIX]{x1D701}^{\prime }}(c_{2,\unicode[STIX]{x1D701}^{\prime }}^{2(q-1)}+1)={\displaystyle \frac{q}{2}}\unicode[STIX]{x1D71B}^{1/(4q^{4})},\end{eqnarray}$$
and
![]() $b_{2,\unicode[STIX]{x1D701}^{\prime }}$
such that
$b_{2,\unicode[STIX]{x1D701}^{\prime }}$
such that
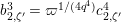 $b_{2,\unicode[STIX]{x1D701}^{\prime }}^{3}=\unicode[STIX]{x1D71B}^{1/(4q^{4})}c_{2,\unicode[STIX]{x1D701}^{\prime }}^{4}$
. We put
$b_{2,\unicode[STIX]{x1D701}^{\prime }}^{3}=\unicode[STIX]{x1D71B}^{1/(4q^{4})}c_{2,\unicode[STIX]{x1D701}^{\prime }}^{4}$
. We put
 $$\begin{eqnarray}a_{1,\unicode[STIX]{x1D701}^{\prime }}=\unicode[STIX]{x1D71B}^{1/(8q^{4})}c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q},\qquad b_{1,\unicode[STIX]{x1D701}^{\prime }}=c_{2,\unicode[STIX]{x1D701}^{\prime }}^{(2q-3)/2}b_{2,\unicode[STIX]{x1D701}^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}a_{1,\unicode[STIX]{x1D701}^{\prime }}=\unicode[STIX]{x1D71B}^{1/(8q^{4})}c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q},\qquad b_{1,\unicode[STIX]{x1D701}^{\prime }}=c_{2,\unicode[STIX]{x1D701}^{\prime }}^{(2q-3)/2}b_{2,\unicode[STIX]{x1D701}^{\prime }}.\end{eqnarray}$$
For each
![]() $\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
, we define a subspace
$\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
, we define a subspace
 ${\mathcal{D}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}\subset \mathbf{P}_{\unicode[STIX]{x1D701}}^{0}$
by
${\mathcal{D}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}\subset \mathbf{P}_{\unicode[STIX]{x1D701}}^{0}$
by
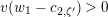 $v(w_{1}-c_{2,\unicode[STIX]{x1D701}^{\prime }})>0$
. Furthermore, we define
$v(w_{1}-c_{2,\unicode[STIX]{x1D701}^{\prime }})>0$
. Furthermore, we define
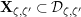 $\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}\subset {\mathcal{D}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
by
$\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}\subset {\mathcal{D}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
by
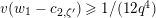 $v(w_{1}-c_{2,\unicode[STIX]{x1D701}^{\prime }})\geqslant 1/(12q^{4})$
. We put
$v(w_{1}-c_{2,\unicode[STIX]{x1D701}^{\prime }})\geqslant 1/(12q^{4})$
. We put
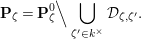 $$\begin{eqnarray}\mathbf{P}_{\unicode[STIX]{x1D701}}=\mathbf{P}_{\unicode[STIX]{x1D701}}^{0}\Big\backslash\mathop{\bigcup }_{\unicode[STIX]{x1D701}^{\prime }\in k^{\times }}{\mathcal{D}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{P}_{\unicode[STIX]{x1D701}}=\mathbf{P}_{\unicode[STIX]{x1D701}}^{0}\Big\backslash\mathop{\bigcup }_{\unicode[STIX]{x1D701}^{\prime }\in k^{\times }}{\mathcal{D}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}.\end{eqnarray}$$
We take
 $(\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime })\in k_{2}^{\times }\times k^{\times }$
and compute the reduction of
$(\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime })\in k_{2}^{\times }\times k^{\times }$
and compute the reduction of
![]() $\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
. In the following, we omit the subscript
$\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
. In the following, we omit the subscript
![]() $\unicode[STIX]{x1D701}^{\prime }$
of
$\unicode[STIX]{x1D701}^{\prime }$
of
![]() $a_{1,\unicode[STIX]{x1D701}^{\prime }}$
,
$a_{1,\unicode[STIX]{x1D701}^{\prime }}$
,
![]() $b_{1,\unicode[STIX]{x1D701}^{\prime }}$
,
$b_{1,\unicode[STIX]{x1D701}^{\prime }}$
,
![]() $b_{2,\unicode[STIX]{x1D701}^{\prime }}$
$b_{2,\unicode[STIX]{x1D701}^{\prime }}$
![]() $c_{1,\unicode[STIX]{x1D701}^{\prime }}$
and
$c_{1,\unicode[STIX]{x1D701}^{\prime }}$
and
![]() $c_{2,\unicode[STIX]{x1D701}^{\prime }}$
, if there is no confusion. We change variables as
$c_{2,\unicode[STIX]{x1D701}^{\prime }}$
, if there is no confusion. We change variables as
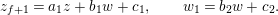 $$\begin{eqnarray}z_{f+1}=a_{1}z+b_{1}w+c_{1},\qquad w_{1}=b_{2}w+c_{2}.\end{eqnarray}$$
$$\begin{eqnarray}z_{f+1}=a_{1}z+b_{1}w+c_{1},\qquad w_{1}=b_{2}w+c_{2}.\end{eqnarray}$$
By substituting these into (4.31), we acquire
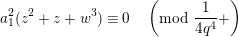 $$\begin{eqnarray}a_{1}^{2}(z^{2}+z+w^{3})\equiv 0\quad \left(\text{mod}~{\displaystyle \frac{1}{4q^{4}}}+\right)\end{eqnarray}$$
$$\begin{eqnarray}a_{1}^{2}(z^{2}+z+w^{3})\equiv 0\quad \left(\text{mod}~{\displaystyle \frac{1}{4q^{4}}}+\right)\end{eqnarray}$$
by the definition of
![]() $a_{1}$
,
$a_{1}$
,
![]() $b_{1}$
,
$b_{1}$
,
![]() $b_{2}$
,
$b_{2}$
,
![]() $c_{1}$
and
$c_{1}$
and
![]() $c_{2}$
.
$c_{2}$
.
Proposition 4.10. For each
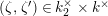 $(\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime })\in k_{2}^{\times }\times k^{\times }$
, the reduction of
$(\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime })\in k_{2}^{\times }\times k^{\times }$
, the reduction of
![]() $\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
is isomorphic to the affine curve defined by
$\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
is isomorphic to the affine curve defined by
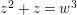 $z^{2}+z=w^{3}$
, and the complement
$z^{2}+z=w^{3}$
, and the complement
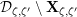 ${\mathcal{D}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}\setminus \mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
is an open annulus.
${\mathcal{D}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}\setminus \mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
is an open annulus.
Proof. The first assertion follows from (4.34). We prove the second assertion. We change variables as
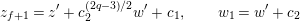 $$\begin{eqnarray}z_{f+1}=z^{\prime }+c_{2}^{(2q-3)/2}w^{\prime }+c_{1},\qquad w_{1}=w^{\prime }+c_{2}\end{eqnarray}$$
$$\begin{eqnarray}z_{f+1}=z^{\prime }+c_{2}^{(2q-3)/2}w^{\prime }+c_{1},\qquad w_{1}=w^{\prime }+c_{2}\end{eqnarray}$$
with
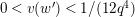 $0<v(w^{\prime })<1/(12q^{4})$
. Substituting them into (4.31), we acquire
$0<v(w^{\prime })<1/(12q^{4})$
. Substituting them into (4.31), we acquire
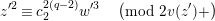 $$\begin{eqnarray}z^{\prime 2}\equiv c_{2}^{2(q-2)}w^{\prime 3}\quad \left(\text{mod}~2v(z^{\prime })+\right)\end{eqnarray}$$
$$\begin{eqnarray}z^{\prime 2}\equiv c_{2}^{2(q-2)}w^{\prime 3}\quad \left(\text{mod}~2v(z^{\prime })+\right)\end{eqnarray}$$
by the choice of
![]() $c_{2}$
. Note that we have
$c_{2}$
. Note that we have
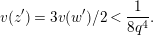 $$\begin{eqnarray}v(z^{\prime })=3v(w^{\prime })/2<{\displaystyle \frac{1}{8q^{4}}}.\end{eqnarray}$$
$$\begin{eqnarray}v(z^{\prime })=3v(w^{\prime })/2<{\displaystyle \frac{1}{8q^{4}}}.\end{eqnarray}$$
By setting
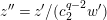 $z^{\prime \prime }=z^{\prime }/(c_{2}^{q-2}w^{\prime })$
, we obtain
$z^{\prime \prime }=z^{\prime }/(c_{2}^{q-2}w^{\prime })$
, we obtain
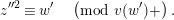 $$\begin{eqnarray}z^{\prime \prime 2}\equiv w^{\prime }\quad \left(\text{mod}~v(w^{\prime })+\right).\end{eqnarray}$$
$$\begin{eqnarray}z^{\prime \prime 2}\equiv w^{\prime }\quad \left(\text{mod}~v(w^{\prime })+\right).\end{eqnarray}$$
Then, we can see that
![]() $z^{\prime }$
and
$z^{\prime }$
and
![]() $w^{\prime }$
are written as functions of
$w^{\prime }$
are written as functions of
![]() $z^{\prime \prime }$
. Hence,
$z^{\prime \prime }$
. Hence,
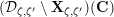 $({\mathcal{D}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}\setminus \mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }})(\mathbf{C})$
is identified with
$({\mathcal{D}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}\setminus \mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }})(\mathbf{C})$
is identified with
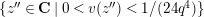 $\{z^{\prime \prime }\in \mathbf{C}\mid 0<v(z^{\prime \prime })<1/(24q^{4})\}$
.◻
$\{z^{\prime \prime }\in \mathbf{C}\mid 0<v(z^{\prime \prime })<1/(24q^{4})\}$
.◻
4.5 Stable covering of
 $\mathbf{X}_{1}(\mathfrak{p}^{3})$
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
In this subsection, we show the existence of the stable covering of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
over some finite extension of the base field
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
over some finite extension of the base field
![]() $\widehat{K}^{\text{ur}}$
. See [Reference Coleman and McMurdyCM, Section 2.3] for the notion of semistable coverings. A semistable covering is called stable, if the corresponding semistable model is stable.
$\widehat{K}^{\text{ur}}$
. See [Reference Coleman and McMurdyCM, Section 2.3] for the notion of semistable coverings. A semistable covering is called stable, if the corresponding semistable model is stable.
Proposition 4.11. There exists a stable covering of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
over a finite extension of the base field.
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
over a finite extension of the base field.
Proof. First, we show that, after taking a finite extension of the base field,
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
is a wide open space. By [Reference StrauchSt1, Theorem 2.3.1(i)],
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
is a wide open space. By [Reference StrauchSt1, Theorem 2.3.1(i)],
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
is the Raynaud generic fiber of the formal completion of an affine scheme over
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
is the Raynaud generic fiber of the formal completion of an affine scheme over
![]() ${\mathcal{O}}_{\widehat{K}^{\text{ur}}}$
at a closed point on the special fiber. Then, we can apply [Reference Coleman and McMurdyCM, Theorem 2.29] to the formal completion of the affine scheme along its special fiber, after shrinking the affine scheme. Hence,
${\mathcal{O}}_{\widehat{K}^{\text{ur}}}$
at a closed point on the special fiber. Then, we can apply [Reference Coleman and McMurdyCM, Theorem 2.29] to the formal completion of the affine scheme along its special fiber, after shrinking the affine scheme. Hence,
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
is a wide open space over some extension.
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
is a wide open space over some extension.
By [Reference Coleman and McMurdyCM, Theorem 2.18], a wide open space can be embedded to a proper algebraic curve so that its complement is a disjoint union of closed disks. Therefore,
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
has a semistable covering over some finite extension by [Reference Coleman and McMurdyCM, Theorem 2.40]. Then, a simple modification gives a stable covering.◻
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
has a semistable covering over some finite extension by [Reference Coleman and McMurdyCM, Theorem 2.40]. Then, a simple modification gives a stable covering.◻
In the following, we construct a candidate of a semistable covering of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
over some finite extension. We put
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
over some finite extension. We put
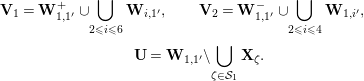 $$\begin{eqnarray}\displaystyle & \displaystyle \mathbf{V}_{1}=\mathbf{W}_{1,1^{\prime }}^{+}\cup \!\mathop{\bigcup }_{2\leqslant i\leqslant 6}\mathbf{W}_{i,1^{\prime }},\qquad \mathbf{V}_{2}=\mathbf{W}_{1,1^{\prime }}^{-}\cup \!\mathop{\bigcup }_{2\leqslant i\leqslant 4}\mathbf{W}_{1,i^{\prime }},\qquad & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{U}=\mathbf{W}_{1,1^{\prime }}\backslash \!\mathop{\bigcup }_{\unicode[STIX]{x1D701}\in {\mathcal{S}}_{1}}\mathbf{X}_{\unicode[STIX]{x1D701}}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathbf{V}_{1}=\mathbf{W}_{1,1^{\prime }}^{+}\cup \!\mathop{\bigcup }_{2\leqslant i\leqslant 6}\mathbf{W}_{i,1^{\prime }},\qquad \mathbf{V}_{2}=\mathbf{W}_{1,1^{\prime }}^{-}\cup \!\mathop{\bigcup }_{2\leqslant i\leqslant 4}\mathbf{W}_{1,i^{\prime }},\qquad & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbf{U}=\mathbf{W}_{1,1^{\prime }}\backslash \!\mathop{\bigcup }_{\unicode[STIX]{x1D701}\in {\mathcal{S}}_{1}}\mathbf{X}_{\unicode[STIX]{x1D701}}. & \displaystyle \nonumber\end{eqnarray}$$
We note that
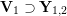 $\mathbf{V}_{1}\supset \mathbf{Y}_{1,2}$
,
$\mathbf{V}_{1}\supset \mathbf{Y}_{1,2}$
,
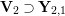 $\mathbf{V}_{2}\supset \mathbf{Y}_{2,1}$
,
$\mathbf{V}_{2}\supset \mathbf{Y}_{2,1}$
,
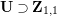 $\mathbf{U}\supset \mathbf{Z}_{1,1}$
,
$\mathbf{U}\supset \mathbf{Z}_{1,1}$
,
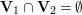 $\mathbf{V}_{1}\cap \mathbf{V}_{2}=\emptyset$
,
$\mathbf{V}_{1}\cap \mathbf{V}_{2}=\emptyset$
,
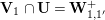 $\mathbf{V}_{1}\cap \mathbf{U}=\mathbf{W}_{1,1^{\prime }}^{+}$
and
$\mathbf{V}_{1}\cap \mathbf{U}=\mathbf{W}_{1,1^{\prime }}^{+}$
and
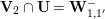 $\mathbf{V}_{2}\cap \mathbf{U}=\mathbf{W}_{1,1^{\prime }}^{-}$
.
$\mathbf{V}_{2}\cap \mathbf{U}=\mathbf{W}_{1,1^{\prime }}^{-}$
.
We consider the case where
![]() $q$
is even in this paragraph. We set
$q$
is even in this paragraph. We set
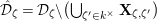 $\hat{{\mathcal{D}}}_{\unicode[STIX]{x1D701}}={\mathcal{D}}_{\unicode[STIX]{x1D701}}\backslash (\bigcup _{\unicode[STIX]{x1D701}^{\prime }\in k^{\times }}\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }})$
for
$\hat{{\mathcal{D}}}_{\unicode[STIX]{x1D701}}={\mathcal{D}}_{\unicode[STIX]{x1D701}}\backslash (\bigcup _{\unicode[STIX]{x1D701}^{\prime }\in k^{\times }}\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }})$
for
![]() $\unicode[STIX]{x1D701}\in k_{2}^{\times }$
. Then,
$\unicode[STIX]{x1D701}\in k_{2}^{\times }$
. Then,
![]() $\hat{{\mathcal{D}}}_{\unicode[STIX]{x1D701}}$
contains
$\hat{{\mathcal{D}}}_{\unicode[STIX]{x1D701}}$
contains
![]() $\mathbf{P}_{\unicode[STIX]{x1D701}}$
as the underlying affinoid. On the other hand, for
$\mathbf{P}_{\unicode[STIX]{x1D701}}$
as the underlying affinoid. On the other hand, for
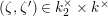 $(\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime })\in k_{2}^{\times }\times k^{\times }$
, the space
$(\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime })\in k_{2}^{\times }\times k^{\times }$
, the space
![]() ${\mathcal{D}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
has the underlying affinoid
${\mathcal{D}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
has the underlying affinoid
![]() $\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
.
$\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
.
We put
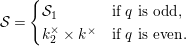 $$\begin{eqnarray}{\mathcal{S}}=\left\{\begin{array}{@{}ll@{}}{\mathcal{S}}_{1}\quad & \text{if }q\text{ is odd},\\ k_{2}^{\times }\times k^{\times }\quad & \text{if }q\text{ is even}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{S}}=\left\{\begin{array}{@{}ll@{}}{\mathcal{S}}_{1}\quad & \text{if }q\text{ is odd},\\ k_{2}^{\times }\times k^{\times }\quad & \text{if }q\text{ is even}.\end{array}\right.\end{eqnarray}$$
Now, we define an admissible covering of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
as
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
as
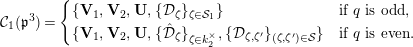 $$\begin{eqnarray}{\mathcal{C}}_{1}(\mathfrak{p}^{3})=\left\{\begin{array}{@{}ll@{}}\{\mathbf{V}_{1},\mathbf{V}_{2},\mathbf{U},\{{\mathcal{D}}_{\unicode[STIX]{x1D701}}\}_{\unicode[STIX]{x1D701}\in {\mathcal{S}}_{1}}\}\quad & \text{if }q\text{ is odd},\\ \{\mathbf{V}_{1},\mathbf{V}_{2},\mathbf{U},\{\hat{{\mathcal{D}}}_{\unicode[STIX]{x1D701}}\}_{\unicode[STIX]{x1D701}\in k_{2}^{\times }},\{{\mathcal{D}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}\}_{(\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime })\in {\mathcal{S}}}\}\quad & \text{if }q\text{ is even}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}_{1}(\mathfrak{p}^{3})=\left\{\begin{array}{@{}ll@{}}\{\mathbf{V}_{1},\mathbf{V}_{2},\mathbf{U},\{{\mathcal{D}}_{\unicode[STIX]{x1D701}}\}_{\unicode[STIX]{x1D701}\in {\mathcal{S}}_{1}}\}\quad & \text{if }q\text{ is odd},\\ \{\mathbf{V}_{1},\mathbf{V}_{2},\mathbf{U},\{\hat{{\mathcal{D}}}_{\unicode[STIX]{x1D701}}\}_{\unicode[STIX]{x1D701}\in k_{2}^{\times }},\{{\mathcal{D}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}\}_{(\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime })\in {\mathcal{S}}}\}\quad & \text{if }q\text{ is even}.\end{array}\right.\end{eqnarray}$$
In Section 7.2, we show that
![]() ${\mathcal{C}}_{1}(\mathfrak{p}^{3})$
is a semistable covering of
${\mathcal{C}}_{1}(\mathfrak{p}^{3})$
is a semistable covering of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
over some finite extension.
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
over some finite extension.
5 Action of the division algebra on the reductions
In this section, we determine the action of
![]() ${\mathcal{O}}_{D}^{\times }$
on the reductions
${\mathcal{O}}_{D}^{\times }$
on the reductions
![]() $\overline{\mathbf{Y}}_{1,2}$
,
$\overline{\mathbf{Y}}_{1,2}$
,
![]() $\overline{\mathbf{Y}}_{2,1}$
$\overline{\mathbf{Y}}_{2,1}$
![]() $\overline{\mathbf{Z}}_{1,1}$
,
$\overline{\mathbf{Z}}_{1,1}$
,
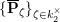 $\{\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}\}_{\unicode[STIX]{x1D701}\in k_{2}^{\times }}$
and
$\{\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}\}_{\unicode[STIX]{x1D701}\in k_{2}^{\times }}$
and
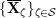 $\{\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}\}_{\unicode[STIX]{x1D701}\in {\mathcal{S}}}$
by using the description of
$\{\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}\}_{\unicode[STIX]{x1D701}\in {\mathcal{S}}}$
by using the description of
![]() ${\mathcal{O}}_{D}^{\times }$
-action in (1.8). We take
${\mathcal{O}}_{D}^{\times }$
-action in (1.8). We take
 $$\begin{eqnarray}d=d_{1}+\unicode[STIX]{x1D711}d_{2}\in {\mathcal{O}}_{D}^{\times },\end{eqnarray}$$
$$\begin{eqnarray}d=d_{1}+\unicode[STIX]{x1D711}d_{2}\in {\mathcal{O}}_{D}^{\times },\end{eqnarray}$$
where
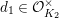 $d_{1}\in {\mathcal{O}}_{K_{2}}^{\times }$
and
$d_{1}\in {\mathcal{O}}_{K_{2}}^{\times }$
and
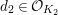 $d_{2}\in {\mathcal{O}}_{K_{2}}$
. We put
$d_{2}\in {\mathcal{O}}_{K_{2}}$
. We put
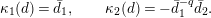 $$\begin{eqnarray}\unicode[STIX]{x1D705}_{1}(d)=\bar{d}_{1},\qquad \unicode[STIX]{x1D705}_{2}(d)=-\bar{d}_{1}^{-q}\bar{d}_{2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}_{1}(d)=\bar{d}_{1},\qquad \unicode[STIX]{x1D705}_{2}(d)=-\bar{d}_{1}^{-q}\bar{d}_{2}.\end{eqnarray}$$
Lemma 5.1. The element
![]() $d$
induces the following morphisms:
$d$
induces the following morphisms:
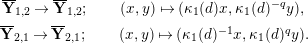 $$\begin{eqnarray}\displaystyle & \overline{\mathbf{Y}}_{1,2}\rightarrow \overline{\mathbf{Y}}_{1,2};\qquad (x,y)\mapsto (\unicode[STIX]{x1D705}_{1}(d)x,\unicode[STIX]{x1D705}_{1}(d)^{-q}y), & \displaystyle \nonumber\\ \displaystyle & \overline{\mathbf{Y}}_{2,1}\rightarrow \overline{\mathbf{Y}}_{2,1};\qquad (x,y)\mapsto (\unicode[STIX]{x1D705}_{1}(d)^{-1}x,\unicode[STIX]{x1D705}_{1}(d)^{q}y). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \overline{\mathbf{Y}}_{1,2}\rightarrow \overline{\mathbf{Y}}_{1,2};\qquad (x,y)\mapsto (\unicode[STIX]{x1D705}_{1}(d)x,\unicode[STIX]{x1D705}_{1}(d)^{-q}y), & \displaystyle \nonumber\\ \displaystyle & \overline{\mathbf{Y}}_{2,1}\rightarrow \overline{\mathbf{Y}}_{2,1};\qquad (x,y)\mapsto (\unicode[STIX]{x1D705}_{1}(d)^{-1}x,\unicode[STIX]{x1D705}_{1}(d)^{q}y). & \displaystyle \nonumber\end{eqnarray}$$
Proof. We prove the assertion for
![]() $\overline{\mathbf{Y}}_{1,2}$
. By (1.5), we have
$\overline{\mathbf{Y}}_{1,2}$
. By (1.5), we have
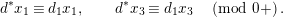 $$\begin{eqnarray}d^{\ast }x_{1}\equiv d_{1}x_{1},\qquad d^{\ast }x_{3}\equiv d_{1}x_{3}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
$$\begin{eqnarray}d^{\ast }x_{1}\equiv d_{1}x_{1},\qquad d^{\ast }x_{3}\equiv d_{1}x_{3}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
Therefore, the required assertion follows from (4.5). The assertion for
![]() $\overline{\mathbf{Y}}_{1,2}$
is proved similarly.◻
$\overline{\mathbf{Y}}_{1,2}$
is proved similarly.◻
Now, let the notation be as in Section 4.3. We put
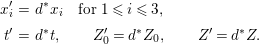 $$\begin{eqnarray}\displaystyle x_{i}^{\prime } & = & \displaystyle d^{\ast }x_{i}\quad \text{for }1\leqslant i\leqslant 3,\nonumber\\ \displaystyle t^{\prime } & = & \displaystyle d^{\ast }t,\qquad Z_{0}^{\prime }=d^{\ast }Z_{0},\qquad Z^{\prime }=d^{\ast }Z.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{i}^{\prime } & = & \displaystyle d^{\ast }x_{i}\quad \text{for }1\leqslant i\leqslant 3,\nonumber\\ \displaystyle t^{\prime } & = & \displaystyle d^{\ast }t,\qquad Z_{0}^{\prime }=d^{\ast }Z_{0},\qquad Z^{\prime }=d^{\ast }Z.\nonumber\end{eqnarray}$$
We have
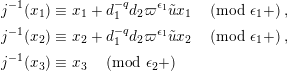 $$\begin{eqnarray}\displaystyle j^{-1}(x_{1}) & \equiv & \displaystyle x_{1}+d_{1}^{-q}d_{2}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{1}}\tilde{u} x_{1}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right),\nonumber\\ \displaystyle j^{-1}(x_{2}) & \equiv & \displaystyle x_{2}+d_{1}^{-q}d_{2}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{1}}\tilde{u} x_{2}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right),\nonumber\\ \displaystyle j^{-1}(x_{3}) & \equiv & \displaystyle x_{3}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle j^{-1}(x_{1}) & \equiv & \displaystyle x_{1}+d_{1}^{-q}d_{2}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{1}}\tilde{u} x_{1}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right),\nonumber\\ \displaystyle j^{-1}(x_{2}) & \equiv & \displaystyle x_{2}+d_{1}^{-q}d_{2}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{1}}\tilde{u} x_{2}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right),\nonumber\\ \displaystyle j^{-1}(x_{3}) & \equiv & \displaystyle x_{3}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right)\nonumber\end{eqnarray}$$
by (1.11). On the other hand, we have
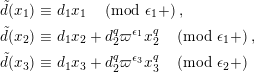 $$\begin{eqnarray}\displaystyle \tilde{d}(x_{1}) & \equiv & \displaystyle d_{1}x_{1}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right),\nonumber\\ \displaystyle \tilde{d}(x_{2}) & \equiv & \displaystyle d_{1}x_{2}+d_{2}^{q}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{1}}x_{2}^{q}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right),\nonumber\\ \displaystyle \tilde{d}(x_{3}) & \equiv & \displaystyle d_{1}x_{3}+d_{2}^{q}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{3}}x_{3}^{q}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{d}(x_{1}) & \equiv & \displaystyle d_{1}x_{1}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right),\nonumber\\ \displaystyle \tilde{d}(x_{2}) & \equiv & \displaystyle d_{1}x_{2}+d_{2}^{q}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{1}}x_{2}^{q}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right),\nonumber\\ \displaystyle \tilde{d}(x_{3}) & \equiv & \displaystyle d_{1}x_{3}+d_{2}^{q}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{3}}x_{3}^{q}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right)\nonumber\end{eqnarray}$$
by (1.5). Hence, we obtain
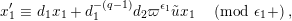 $$\begin{eqnarray}\displaystyle x_{1}^{\prime } & \equiv & \displaystyle d_{1}x_{1}+d_{1}^{-(q-1)}d_{2}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{1}}\tilde{u} x_{1}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{1}^{\prime } & \equiv & \displaystyle d_{1}x_{1}+d_{1}^{-(q-1)}d_{2}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{1}}\tilde{u} x_{1}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right),\end{eqnarray}$$
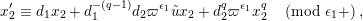 $$\begin{eqnarray}\displaystyle x_{2}^{\prime } & \equiv & \displaystyle d_{1}x_{2}+d_{1}^{-(q-1)}d_{2}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{1}}\tilde{u} x_{2}+d_{2}^{q}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{1}}x_{2}^{q}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{2}^{\prime } & \equiv & \displaystyle d_{1}x_{2}+d_{1}^{-(q-1)}d_{2}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{1}}\tilde{u} x_{2}+d_{2}^{q}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{1}}x_{2}^{q}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right),\end{eqnarray}$$
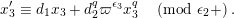 $$\begin{eqnarray}\displaystyle x_{3}^{\prime } & \equiv & \displaystyle d_{1}x_{3}+d_{2}^{q}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{3}}x_{3}^{q}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{3}^{\prime } & \equiv & \displaystyle d_{1}x_{3}+d_{2}^{q}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{3}}x_{3}^{q}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right).\end{eqnarray}$$
By the definition of
![]() $t$
and the equation
$t$
and the equation
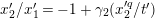 $x_{2}^{\prime }/x_{1}^{\prime }=-1+\unicode[STIX]{x1D6FE}_{2}(x_{2}^{\prime q}/t^{\prime })$
, we acquire
$x_{2}^{\prime }/x_{1}^{\prime }=-1+\unicode[STIX]{x1D6FE}_{2}(x_{2}^{\prime q}/t^{\prime })$
, we acquire
 $$\begin{eqnarray}t^{\prime }\equiv d_{1}^{q}t-d_{1}^{q-1}d_{2}^{q}t^{2-q}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{2}}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right)\end{eqnarray}$$
$$\begin{eqnarray}t^{\prime }\equiv d_{1}^{q}t-d_{1}^{q-1}d_{2}^{q}t^{2-q}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{2}}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right)\end{eqnarray}$$
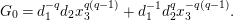 $$\begin{eqnarray}G_{0}=d_{1}^{-q}d_{2}x_{3}^{q(q-1)}+d_{1}^{-1}d_{2}^{q}x_{3}^{-q(q-1)}.\end{eqnarray}$$
$$\begin{eqnarray}G_{0}=d_{1}^{-q}d_{2}x_{3}^{q(q-1)}+d_{1}^{-1}d_{2}^{q}x_{3}^{-q(q-1)}.\end{eqnarray}$$
By the definition of
![]() $Z_{0}$
and the equation
$Z_{0}$
and the equation
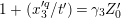 $1+(x_{3}^{\prime q}/t^{\prime })=\unicode[STIX]{x1D6FE}_{3}Z_{0}^{\prime }$
, we obtain
$1+(x_{3}^{\prime q}/t^{\prime })=\unicode[STIX]{x1D6FE}_{3}Z_{0}^{\prime }$
, we obtain
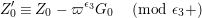 $$\begin{eqnarray}Z_{0}^{\prime }\equiv Z_{0}-\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{3}}G_{0}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{3}+\right)\end{eqnarray}$$
$$\begin{eqnarray}Z_{0}^{\prime }\equiv Z_{0}-\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{3}}G_{0}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{3}+\right)\end{eqnarray}$$
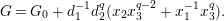 $$\begin{eqnarray}G=G_{0}+d_{1}^{-1}d_{2}^{q}(x_{2}x_{3}^{q-2}+x_{1}^{-1}x_{3}^{q}).\end{eqnarray}$$
$$\begin{eqnarray}G=G_{0}+d_{1}^{-1}d_{2}^{q}(x_{2}x_{3}^{q-2}+x_{1}^{-1}x_{3}^{q}).\end{eqnarray}$$
By the definition of
![]() $Z$
and the equation
$Z$
and the equation
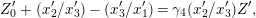 $$\begin{eqnarray}Z_{0}^{\prime }+(x_{2}^{\prime }/x_{3}^{\prime })-(x_{3}^{\prime }/x_{1}^{\prime })=\unicode[STIX]{x1D6FE}_{4}(x_{2}^{\prime }/x_{3}^{\prime })Z^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}Z_{0}^{\prime }+(x_{2}^{\prime }/x_{3}^{\prime })-(x_{3}^{\prime }/x_{1}^{\prime })=\unicode[STIX]{x1D6FE}_{4}(x_{2}^{\prime }/x_{3}^{\prime })Z^{\prime },\end{eqnarray}$$
we obtain
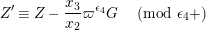 $$\begin{eqnarray}Z^{\prime }\equiv Z-{\displaystyle \frac{x_{3}}{x_{2}}}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{4}}G\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{4}+\right)\end{eqnarray}$$
$$\begin{eqnarray}Z^{\prime }\equiv Z-{\displaystyle \frac{x_{3}}{x_{2}}}\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{4}}G\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{4}+\right)\end{eqnarray}$$
using (5.1), (5.2), (5.3) and (5.5). We have
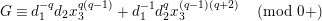 $$\begin{eqnarray}G\equiv d_{1}^{-q}d_{2}x_{3}^{q(q-1)}+d_{1}^{-1}d_{2}^{q}x_{3}^{(q-1)(q+2)}\quad \left(\text{mod}~0+\right)\end{eqnarray}$$
$$\begin{eqnarray}G\equiv d_{1}^{-q}d_{2}x_{3}^{q(q-1)}+d_{1}^{-1}d_{2}^{q}x_{3}^{(q-1)(q+2)}\quad \left(\text{mod}~0+\right)\end{eqnarray}$$
by
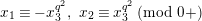 $x_{1}\equiv -x_{3}^{q^{2}},~x_{2}\equiv x_{3}^{q^{2}}\;(\text{mod}~0+)$
. We put
$x_{1}\equiv -x_{3}^{q^{2}},~x_{2}\equiv x_{3}^{q^{2}}\;(\text{mod}~0+)$
. We put
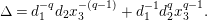 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}=d_{1}^{-q}d_{2}x_{3}^{-(q-1)}+d_{1}^{-1}d_{2}^{q}x_{3}^{q-1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}=d_{1}^{-q}d_{2}x_{3}^{-(q-1)}+d_{1}^{-1}d_{2}^{q}x_{3}^{q-1}.\end{eqnarray}$$
Then, the congruence (5.6) has the following form:
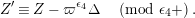 $$\begin{eqnarray}Z^{\prime }\equiv Z-\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{4}}\unicode[STIX]{x1D6E5}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{4}+\right).\end{eqnarray}$$
$$\begin{eqnarray}Z^{\prime }\equiv Z-\unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{4}}\unicode[STIX]{x1D6E5}\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{4}+\right).\end{eqnarray}$$
Proposition 5.2. The element
![]() $d$
acts on
$d$
acts on
![]() $\overline{\mathbf{Z}}_{1,1}$
by
$\overline{\mathbf{Z}}_{1,1}$
by
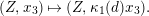 $$\begin{eqnarray}(Z,x_{3})\mapsto (Z,\unicode[STIX]{x1D705}_{1}(d)x_{3}).\end{eqnarray}$$
$$\begin{eqnarray}(Z,x_{3})\mapsto (Z,\unicode[STIX]{x1D705}_{1}(d)x_{3}).\end{eqnarray}$$
Proposition 5.3. The element
![]() $d$
induces the morphism
$d$
induces the morphism
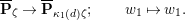 $$\begin{eqnarray}\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}\rightarrow \overline{\mathbf{P}}_{\unicode[STIX]{x1D705}_{1}(d)\unicode[STIX]{x1D701}};\qquad w_{1}\mapsto w_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}\rightarrow \overline{\mathbf{P}}_{\unicode[STIX]{x1D705}_{1}(d)\unicode[STIX]{x1D701}};\qquad w_{1}\mapsto w_{1}.\end{eqnarray}$$
Proposition 5.4. We take
![]() $\unicode[STIX]{x1D701}\in {\mathcal{S}}_{1}$
. Further, we take
$\unicode[STIX]{x1D701}\in {\mathcal{S}}_{1}$
. Further, we take
![]() $\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
, if
$\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
, if
![]() $q$
is even. We set as follows:
$q$
is even. We set as follows:
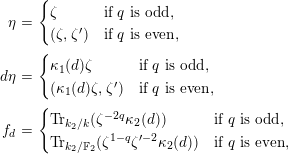 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D701}\quad & \text{if }q\text{ is odd},\\ (\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime })\quad & \text{if }q\text{is even},\end{array}\right.\nonumber\\ \displaystyle d\unicode[STIX]{x1D702} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D705}_{1}(d)\unicode[STIX]{x1D701}\quad & \text{if }q\text{ is odd},\\ (\unicode[STIX]{x1D705}_{1}(d)\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime })\quad & \text{if }q\text{ is even},\end{array}\right.\nonumber\\ \displaystyle f_{d} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\text{Tr}_{k_{2}/k}(\unicode[STIX]{x1D701}^{-2q}\unicode[STIX]{x1D705}_{2}(d))\quad & \text{if }q\text{ is odd},\\ \text{Tr}_{k_{2}/\mathbb{F}_{2}}(\unicode[STIX]{x1D701}^{1-q}\unicode[STIX]{x1D701}^{\prime -2}\unicode[STIX]{x1D705}_{2}(d))\quad & \text{if }q\text{ is even},\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D701}\quad & \text{if }q\text{ is odd},\\ (\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime })\quad & \text{if }q\text{is even},\end{array}\right.\nonumber\\ \displaystyle d\unicode[STIX]{x1D702} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D705}_{1}(d)\unicode[STIX]{x1D701}\quad & \text{if }q\text{ is odd},\\ (\unicode[STIX]{x1D705}_{1}(d)\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime })\quad & \text{if }q\text{ is even},\end{array}\right.\nonumber\\ \displaystyle f_{d} & = & \displaystyle \left\{\begin{array}{@{}ll@{}}\text{Tr}_{k_{2}/k}(\unicode[STIX]{x1D701}^{-2q}\unicode[STIX]{x1D705}_{2}(d))\quad & \text{if }q\text{ is odd},\\ \text{Tr}_{k_{2}/\mathbb{F}_{2}}(\unicode[STIX]{x1D701}^{1-q}\unicode[STIX]{x1D701}^{\prime -2}\unicode[STIX]{x1D705}_{2}(d))\quad & \text{if }q\text{ is even},\end{array}\right.\nonumber\end{eqnarray}$$
where
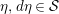 $\unicode[STIX]{x1D702},d\unicode[STIX]{x1D702}\in {\mathcal{S}}$
. Then, the element
$\unicode[STIX]{x1D702},d\unicode[STIX]{x1D702}\in {\mathcal{S}}$
. Then, the element
![]() $d$
induces
$d$
induces
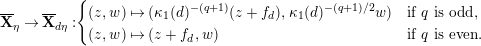 $$\begin{eqnarray}\overline{\mathbf{X}}_{\unicode[STIX]{x1D702}}\rightarrow \overline{\mathbf{X}}_{d\unicode[STIX]{x1D702}}:\!\left\{\begin{array}{@{}ll@{}}(z,w)\mapsto (\unicode[STIX]{x1D705}_{1}(d)^{-(q+1)}(z+f_{d}),\unicode[STIX]{x1D705}_{1}(d)^{-(q+1)/2}w)\quad & \text{if }q\text{ is odd},\\ (z,w)\mapsto (z+f_{d},w)\quad & \text{if }q\text{ is even}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\overline{\mathbf{X}}_{\unicode[STIX]{x1D702}}\rightarrow \overline{\mathbf{X}}_{d\unicode[STIX]{x1D702}}:\!\left\{\begin{array}{@{}ll@{}}(z,w)\mapsto (\unicode[STIX]{x1D705}_{1}(d)^{-(q+1)}(z+f_{d}),\unicode[STIX]{x1D705}_{1}(d)^{-(q+1)/2}w)\quad & \text{if }q\text{ is odd},\\ (z,w)\mapsto (z+f_{d},w)\quad & \text{if }q\text{ is even}.\end{array}\right.\end{eqnarray}$$
Proof. First, we assume that
![]() $q$
is odd. Recall that
$q$
is odd. Recall that
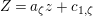 $Z=a_{\unicode[STIX]{x1D701}}z+c_{1,\unicode[STIX]{x1D701}}$
and
$Z=a_{\unicode[STIX]{x1D701}}z+c_{1,\unicode[STIX]{x1D701}}$
and
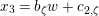 $x_{3}=b_{\unicode[STIX]{x1D701}}w+c_{2,\unicode[STIX]{x1D701}}$
. Similarly, we have
$x_{3}=b_{\unicode[STIX]{x1D701}}w+c_{2,\unicode[STIX]{x1D701}}$
. Similarly, we have
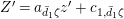 $Z^{\prime }=a_{\bar{d}_{1}\unicode[STIX]{x1D701}}z^{\prime }+c_{1,\bar{d}_{1}\unicode[STIX]{x1D701}}$
and
$Z^{\prime }=a_{\bar{d}_{1}\unicode[STIX]{x1D701}}z^{\prime }+c_{1,\bar{d}_{1}\unicode[STIX]{x1D701}}$
and
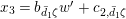 $x_{3}=b_{\bar{d}_{1}\unicode[STIX]{x1D701}}w^{\prime }+c_{2,\bar{d}_{1}\unicode[STIX]{x1D701}}$
. Then, the claim follows from (5.7).
$x_{3}=b_{\bar{d}_{1}\unicode[STIX]{x1D701}}w^{\prime }+c_{2,\bar{d}_{1}\unicode[STIX]{x1D701}}$
. Then, the claim follows from (5.7).
Next, we assume that
![]() $q$
is even. By (5.7) and
$q$
is even. By (5.7) and
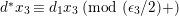 $d^{\ast }x_{3}\equiv d_{1}x_{3}\;(\text{mod}~(\unicode[STIX]{x1D716}_{3}/2)+)$
, we acquire
$d^{\ast }x_{3}\equiv d_{1}x_{3}\;(\text{mod}~(\unicode[STIX]{x1D716}_{3}/2)+)$
, we acquire
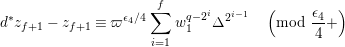 $$\begin{eqnarray}d^{\ast }z_{f+1}-z_{f+1}\equiv \unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{4}/4}\mathop{\sum }_{i=1}^{f}w_{1}^{q-2^{i}}\unicode[STIX]{x1D6E5}^{2^{i-1}}\quad \left(\text{mod}~{\displaystyle \frac{\unicode[STIX]{x1D716}_{4}}{4}}+\right)\end{eqnarray}$$
$$\begin{eqnarray}d^{\ast }z_{f+1}-z_{f+1}\equiv \unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{4}/4}\mathop{\sum }_{i=1}^{f}w_{1}^{q-2^{i}}\unicode[STIX]{x1D6E5}^{2^{i-1}}\quad \left(\text{mod}~{\displaystyle \frac{\unicode[STIX]{x1D716}_{4}}{4}}+\right)\end{eqnarray}$$
on the locus where
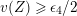 $v(Z)\geqslant \unicode[STIX]{x1D716}_{4}/2$
. By
$v(Z)\geqslant \unicode[STIX]{x1D716}_{4}/2$
. By
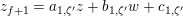 $z_{f+1}=a_{1,\unicode[STIX]{x1D701}^{\prime }}z+b_{1,\unicode[STIX]{x1D701}^{\prime }}w+c_{1,\unicode[STIX]{x1D701}^{\prime }}$
and
$z_{f+1}=a_{1,\unicode[STIX]{x1D701}^{\prime }}z+b_{1,\unicode[STIX]{x1D701}^{\prime }}w+c_{1,\unicode[STIX]{x1D701}^{\prime }}$
and
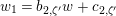 $w_{1}=b_{2,\unicode[STIX]{x1D701}^{\prime }}w+c_{2,\unicode[STIX]{x1D701}^{\prime }}$
, we obtain
$w_{1}=b_{2,\unicode[STIX]{x1D701}^{\prime }}w+c_{2,\unicode[STIX]{x1D701}^{\prime }}$
, we obtain
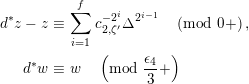 $$\begin{eqnarray}\displaystyle d^{\ast }z-z & \equiv & \displaystyle \mathop{\sum }_{i=1}^{f}c_{2,\unicode[STIX]{x1D701}^{\prime }}^{-2^{i}}\unicode[STIX]{x1D6E5}^{2^{i-1}}\quad \left(\text{mod}~0+\right),\nonumber\\ \displaystyle d^{\ast }w & \equiv & \displaystyle w\quad \left(\text{mod}~{\displaystyle \frac{\unicode[STIX]{x1D716}_{4}}{3}}+\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d^{\ast }z-z & \equiv & \displaystyle \mathop{\sum }_{i=1}^{f}c_{2,\unicode[STIX]{x1D701}^{\prime }}^{-2^{i}}\unicode[STIX]{x1D6E5}^{2^{i-1}}\quad \left(\text{mod}~0+\right),\nonumber\\ \displaystyle d^{\ast }w & \equiv & \displaystyle w\quad \left(\text{mod}~{\displaystyle \frac{\unicode[STIX]{x1D716}_{4}}{3}}+\right)\nonumber\end{eqnarray}$$
on
![]() $\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
by (5.7) and (5.8). On the other hand, we have
$\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
by (5.7) and (5.8). On the other hand, we have
 $$\begin{eqnarray}\mathop{\sum }_{i=1}^{f}\bar{c}_{2,\unicode[STIX]{x1D701}^{\prime }}^{-2^{i}}\overline{\unicode[STIX]{x1D6E5}}^{2^{i-1}}=f_{d},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{f}\bar{c}_{2,\unicode[STIX]{x1D701}^{\prime }}^{-2^{i}}\overline{\unicode[STIX]{x1D6E5}}^{2^{i-1}}=f_{d},\end{eqnarray}$$
because
![]() $\bar{x_{3}}=\unicode[STIX]{x1D701}$
and
$\bar{x_{3}}=\unicode[STIX]{x1D701}$
and
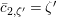 $\bar{c}_{2,\unicode[STIX]{x1D701}^{\prime }}=\unicode[STIX]{x1D701}^{\prime }$
. Hence, we have proved the claim.◻
$\bar{c}_{2,\unicode[STIX]{x1D701}^{\prime }}=\unicode[STIX]{x1D701}^{\prime }$
. Hence, we have proved the claim.◻
6 Action of the Weil group on the reductions
In this section, we compute the actions of the Weil group on the reductions
![]() $\overline{\mathbf{Y}}_{1,2}$
,
$\overline{\mathbf{Y}}_{1,2}$
,
![]() $\overline{\mathbf{Y}}_{2,1}$
,
$\overline{\mathbf{Y}}_{2,1}$
,
![]() $\overline{\mathbf{Z}}_{1,1}$
,
$\overline{\mathbf{Z}}_{1,1}$
,
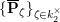 $\{\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}\}_{\unicode[STIX]{x1D701}\in k_{2}^{\times }}$
and
$\{\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}\}_{\unicode[STIX]{x1D701}\in k_{2}^{\times }}$
and
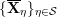 $\{\overline{\mathbf{X}}_{\unicode[STIX]{x1D702}}\}_{\unicode[STIX]{x1D702}\in {\mathcal{S}}}$
.
$\{\overline{\mathbf{X}}_{\unicode[STIX]{x1D702}}\}_{\unicode[STIX]{x1D702}\in {\mathcal{S}}}$
.
Let
![]() $\mathbf{X}$
be a reduced affinoid over
$\mathbf{X}$
be a reduced affinoid over
![]() $\mathbf{C}$
with an action of
$\mathbf{C}$
with an action of
![]() $W_{K}$
. For
$W_{K}$
. For
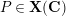 $P\in \mathbf{X}(\mathbf{C})$
, the image of
$P\in \mathbf{X}(\mathbf{C})$
, the image of
![]() $P$
under the natural reduction map
$P$
under the natural reduction map
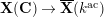 $\mathbf{X}(\mathbf{C})\rightarrow \overline{\mathbf{X}}(k^{\text{ac}})$
is denoted by
$\mathbf{X}(\mathbf{C})\rightarrow \overline{\mathbf{X}}(k^{\text{ac}})$
is denoted by
![]() $\overline{P}$
. The action of
$\overline{P}$
. The action of
![]() $W_{K}$
on
$W_{K}$
on
![]() $\overline{\mathbf{X}}$
is a homomorphism
$\overline{\mathbf{X}}$
is a homomorphism
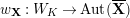 $$\begin{eqnarray}w_{\mathbf{X}}:W_{K}\rightarrow \text{Aut}(\overline{\mathbf{X}})\end{eqnarray}$$
$$\begin{eqnarray}w_{\mathbf{X}}:W_{K}\rightarrow \text{Aut}(\overline{\mathbf{X}})\end{eqnarray}$$
characterized by
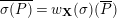 $\overline{\unicode[STIX]{x1D70E}(P)}=w_{\mathbf{X}}(\unicode[STIX]{x1D70E})(\overline{P})$
for
$\overline{\unicode[STIX]{x1D70E}(P)}=w_{\mathbf{X}}(\unicode[STIX]{x1D70E})(\overline{P})$
for
 $\unicode[STIX]{x1D70E}\in W_{K}$
and
$\unicode[STIX]{x1D70E}\in W_{K}$
and
 $P\in \mathbf{X}(\mathbf{C})$
. For
$P\in \mathbf{X}(\mathbf{C})$
. For
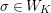 $\unicode[STIX]{x1D70E}\in W_{K}$
, we define
$\unicode[STIX]{x1D70E}\in W_{K}$
, we define
![]() $r_{\unicode[STIX]{x1D70E}}\in \mathbb{Z}$
so that
$r_{\unicode[STIX]{x1D70E}}\in \mathbb{Z}$
so that
![]() $\unicode[STIX]{x1D70E}$
induces the
$\unicode[STIX]{x1D70E}$
induces the
![]() $q^{-r_{\unicode[STIX]{x1D70E}}}$
th power map on the residue field of
$q^{-r_{\unicode[STIX]{x1D70E}}}$
th power map on the residue field of
![]() $K^{\text{ac}}$
.
$K^{\text{ac}}$
.
Remark 6.1. In the usual sense,
![]() $W_{K}$
does not act on
$W_{K}$
does not act on
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
, because the action of
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
, because the action of
![]() $W_{K}$
does not preserve the connected components of
$W_{K}$
does not preserve the connected components of
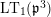 $\text{LT}_{1}(\mathfrak{p}^{3})$
. Precisely,
$\text{LT}_{1}(\mathfrak{p}^{3})$
. Precisely,
![]() $w_{\mathbf{X}}$
is the action of
$w_{\mathbf{X}}$
is the action of
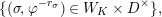 $$\begin{eqnarray}\{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D711}^{-r_{\unicode[STIX]{x1D70E}}})\in W_{K}\times D^{\times }\},\end{eqnarray}$$
$$\begin{eqnarray}\{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D711}^{-r_{\unicode[STIX]{x1D70E}}})\in W_{K}\times D^{\times }\},\end{eqnarray}$$
which preserves the connected components of
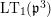 $\text{LT}_{1}(\mathfrak{p}^{3})$
.
$\text{LT}_{1}(\mathfrak{p}^{3})$
.
6.1 Actions of the Weil group on
 $\overline{\mathbf{Y}}_{1,2}$
,
$\overline{\mathbf{Y}}_{1,2}$
,
 $\overline{\mathbf{Y}}_{2,1}$
and
$\overline{\mathbf{Y}}_{2,1}$
and
 $\overline{\mathbf{Z}}_{1,1}$
$\overline{\mathbf{Z}}_{1,1}$
For
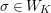 $\unicode[STIX]{x1D70E}\in W_{K}$
, we put
$\unicode[STIX]{x1D70E}\in W_{K}$
, we put
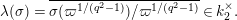 $$\begin{eqnarray}\unicode[STIX]{x1D706}(\unicode[STIX]{x1D70E})=\overline{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}^{1/(q^{2}-1)})/\unicode[STIX]{x1D71B}^{1/(q^{2}-1)}}\in k_{2}^{\times }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}(\unicode[STIX]{x1D70E})=\overline{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}^{1/(q^{2}-1)})/\unicode[STIX]{x1D71B}^{1/(q^{2}-1)}}\in k_{2}^{\times }.\end{eqnarray}$$
We note that
![]() $\unicode[STIX]{x1D706}$
is not a group homomorphism in general.
$\unicode[STIX]{x1D706}$
is not a group homomorphism in general.
Lemma 6.2. Let
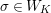 $\unicode[STIX]{x1D70E}\in W_{K}$
. Then, the element
$\unicode[STIX]{x1D70E}\in W_{K}$
. Then, the element
![]() $\unicode[STIX]{x1D70E}$
induces the automorphisms
$\unicode[STIX]{x1D70E}$
induces the automorphisms
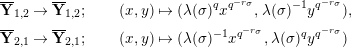 $$\begin{eqnarray}\displaystyle & & \displaystyle \overline{\mathbf{Y}}_{1,2}\rightarrow \overline{\mathbf{Y}}_{1,2};\qquad (x,y)\mapsto (\unicode[STIX]{x1D706}(\unicode[STIX]{x1D70E})^{q}x^{q^{-r_{\unicode[STIX]{x1D70E}}}},\unicode[STIX]{x1D706}(\unicode[STIX]{x1D70E})^{-1}y^{q^{-r_{\unicode[STIX]{x1D70E}}}}),\nonumber\\ \displaystyle & & \displaystyle \overline{\mathbf{Y}}_{2,1}\rightarrow \overline{\mathbf{Y}}_{2,1};\qquad (x,y)\mapsto (\unicode[STIX]{x1D706}(\unicode[STIX]{x1D70E})^{-1}x^{q^{-r_{\unicode[STIX]{x1D70E}}}},\unicode[STIX]{x1D706}(\unicode[STIX]{x1D70E})^{q}y^{q^{-r_{\unicode[STIX]{x1D70E}}}})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \overline{\mathbf{Y}}_{1,2}\rightarrow \overline{\mathbf{Y}}_{1,2};\qquad (x,y)\mapsto (\unicode[STIX]{x1D706}(\unicode[STIX]{x1D70E})^{q}x^{q^{-r_{\unicode[STIX]{x1D70E}}}},\unicode[STIX]{x1D706}(\unicode[STIX]{x1D70E})^{-1}y^{q^{-r_{\unicode[STIX]{x1D70E}}}}),\nonumber\\ \displaystyle & & \displaystyle \overline{\mathbf{Y}}_{2,1}\rightarrow \overline{\mathbf{Y}}_{2,1};\qquad (x,y)\mapsto (\unicode[STIX]{x1D706}(\unicode[STIX]{x1D70E})^{-1}x^{q^{-r_{\unicode[STIX]{x1D70E}}}},\unicode[STIX]{x1D706}(\unicode[STIX]{x1D70E})^{q}y^{q^{-r_{\unicode[STIX]{x1D70E}}}})\nonumber\end{eqnarray}$$
as schemes over
![]() $k$
.
$k$
.
Proof. We prove the claim for
![]() $\overline{\mathbf{Y}}_{1,2}$
. We set
$\overline{\mathbf{Y}}_{1,2}$
. We set
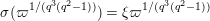 $$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}^{1/(q^{3}(q^{2}-1))})=\unicode[STIX]{x1D709}\unicode[STIX]{x1D71B}^{1/(q^{3}(q^{2}-1))}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}^{1/(q^{3}(q^{2}-1))})=\unicode[STIX]{x1D709}\unicode[STIX]{x1D71B}^{1/(q^{3}(q^{2}-1))}\end{eqnarray}$$
with
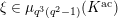 $\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D707}_{q^{3}(q^{2}-1)}(K^{\text{ac}})$
. Let
$\unicode[STIX]{x1D709}\in \unicode[STIX]{x1D707}_{q^{3}(q^{2}-1)}(K^{\text{ac}})$
. Let
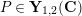 $P\in \mathbf{Y}_{1,2}(\mathbf{C})$
. We have
$P\in \mathbf{Y}_{1,2}(\mathbf{C})$
. We have
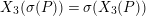 $X_{3}(\unicode[STIX]{x1D70E}(P))=\unicode[STIX]{x1D70E}(X_{3}(P))$
. By applying
$X_{3}(\unicode[STIX]{x1D70E}(P))=\unicode[STIX]{x1D70E}(X_{3}(P))$
. By applying
![]() $\unicode[STIX]{x1D70E}$
to
$\unicode[STIX]{x1D70E}$
to
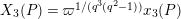 $X_{3}(P)=\unicode[STIX]{x1D71B}^{1/(q^{3}(q^{2}-1))}x_{3}(P)$
, we obtain
$X_{3}(P)=\unicode[STIX]{x1D71B}^{1/(q^{3}(q^{2}-1))}x_{3}(P)$
, we obtain
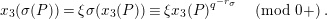 $$\begin{eqnarray}x_{3}(\unicode[STIX]{x1D70E}(P))=\unicode[STIX]{x1D709}\unicode[STIX]{x1D70E}(x_{3}(P))\equiv \unicode[STIX]{x1D709}x_{3}(P)^{q^{-r_{\unicode[STIX]{x1D70E}}}}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
$$\begin{eqnarray}x_{3}(\unicode[STIX]{x1D70E}(P))=\unicode[STIX]{x1D709}\unicode[STIX]{x1D70E}(x_{3}(P))\equiv \unicode[STIX]{x1D709}x_{3}(P)^{q^{-r_{\unicode[STIX]{x1D70E}}}}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
In the same way, we have
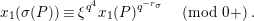 $$\begin{eqnarray}x_{1}(\unicode[STIX]{x1D70E}(P))\equiv \unicode[STIX]{x1D709}^{q^{4}}x_{1}(P)^{q^{-r_{\unicode[STIX]{x1D70E}}}}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
$$\begin{eqnarray}x_{1}(\unicode[STIX]{x1D70E}(P))\equiv \unicode[STIX]{x1D709}^{q^{4}}x_{1}(P)^{q^{-r_{\unicode[STIX]{x1D70E}}}}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
Therefore, we acquire
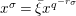 $x^{\unicode[STIX]{x1D70E}}=\bar{\unicode[STIX]{x1D709}}x^{q^{-r_{\unicode[STIX]{x1D70E}}}}$
and
$x^{\unicode[STIX]{x1D70E}}=\bar{\unicode[STIX]{x1D709}}x^{q^{-r_{\unicode[STIX]{x1D70E}}}}$
and
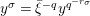 $y^{\unicode[STIX]{x1D70E}}=\bar{\unicode[STIX]{x1D709}}^{-q}y^{q^{-r_{\unicode[STIX]{x1D70E}}}}$
by (4.5). Hence, the claim follows from
$y^{\unicode[STIX]{x1D70E}}=\bar{\unicode[STIX]{x1D709}}^{-q}y^{q^{-r_{\unicode[STIX]{x1D70E}}}}$
by (4.5). Hence, the claim follows from
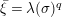 $\bar{\unicode[STIX]{x1D709}}=\unicode[STIX]{x1D706}(\unicode[STIX]{x1D70E})^{q}$
. We can prove the claim for
$\bar{\unicode[STIX]{x1D709}}=\unicode[STIX]{x1D706}(\unicode[STIX]{x1D70E})^{q}$
. We can prove the claim for
![]() $\overline{\mathbf{Y}}_{2,1}$
similarly.◻
$\overline{\mathbf{Y}}_{2,1}$
similarly.◻
For
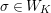 $\unicode[STIX]{x1D70E}\in W_{K}$
, we put
$\unicode[STIX]{x1D70E}\in W_{K}$
, we put
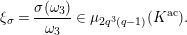 $$\begin{eqnarray}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}={\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D714}_{3})}{\unicode[STIX]{x1D714}_{3}}}\in \unicode[STIX]{x1D707}_{2q^{3}(q-1)}(K^{\text{ac}}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}={\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D714}_{3})}{\unicode[STIX]{x1D714}_{3}}}\in \unicode[STIX]{x1D707}_{2q^{3}(q-1)}(K^{\text{ac}}).\end{eqnarray}$$
Lemma 6.3. Let
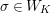 $\unicode[STIX]{x1D70E}\in W_{K}$
. Then,
$\unicode[STIX]{x1D70E}\in W_{K}$
. Then,
![]() $\unicode[STIX]{x1D70E}$
acts on
$\unicode[STIX]{x1D70E}$
acts on
![]() $\overline{\mathbf{Z}}_{1,1}$
by
$\overline{\mathbf{Z}}_{1,1}$
by
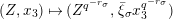 $(Z,x_{3})\mapsto (Z^{q^{-r_{\unicode[STIX]{x1D70E}}}},\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}x_{3}^{q^{-r_{\unicode[STIX]{x1D70E}}}})$
.
$(Z,x_{3})\mapsto (Z^{q^{-r_{\unicode[STIX]{x1D70E}}}},\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}x_{3}^{q^{-r_{\unicode[STIX]{x1D70E}}}})$
.
Proof. We use the notation in Section 4.3. Let
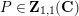 $P\in \mathbf{Z}_{1,1}(\mathbf{C})$
. Since we set
$P\in \mathbf{Z}_{1,1}(\mathbf{C})$
. Since we set
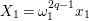 $X_{1}=\unicode[STIX]{x1D714}_{1}^{2q-1}x_{1}$
,
$X_{1}=\unicode[STIX]{x1D714}_{1}^{2q-1}x_{1}$
,
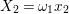 $X_{2}=\unicode[STIX]{x1D714}_{1}x_{2}$
and
$X_{2}=\unicode[STIX]{x1D714}_{1}x_{2}$
and
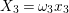 $X_{3}=\unicode[STIX]{x1D714}_{3}x_{3}$
, we have
$X_{3}=\unicode[STIX]{x1D714}_{3}x_{3}$
, we have
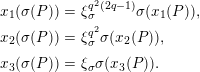 $$\begin{eqnarray}\displaystyle x_{1}(\unicode[STIX]{x1D70E}(P)) & = & \displaystyle \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{q^{2}(2q-1)}\unicode[STIX]{x1D70E}(x_{1}(P)),\nonumber\\ \displaystyle x_{2}(\unicode[STIX]{x1D70E}(P)) & = & \displaystyle \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{q^{2}}\unicode[STIX]{x1D70E}(x_{2}(P)),\nonumber\\ \displaystyle x_{3}(\unicode[STIX]{x1D70E}(P)) & = & \displaystyle \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(x_{3}(P)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{1}(\unicode[STIX]{x1D70E}(P)) & = & \displaystyle \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{q^{2}(2q-1)}\unicode[STIX]{x1D70E}(x_{1}(P)),\nonumber\\ \displaystyle x_{2}(\unicode[STIX]{x1D70E}(P)) & = & \displaystyle \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{q^{2}}\unicode[STIX]{x1D70E}(x_{2}(P)),\nonumber\\ \displaystyle x_{3}(\unicode[STIX]{x1D70E}(P)) & = & \displaystyle \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(x_{3}(P)).\nonumber\end{eqnarray}$$
Hence, we obtain
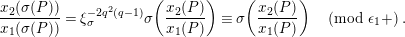 $$\begin{eqnarray}{\displaystyle \frac{x_{2}(\unicode[STIX]{x1D70E}(P))}{x_{1}(\unicode[STIX]{x1D70E}(P))}}=\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{-2q^{2}(q-1)}\unicode[STIX]{x1D70E}\biggl({\displaystyle \frac{x_{2}(P)}{x_{1}(P)}}\biggr)\equiv \unicode[STIX]{x1D70E}\biggl({\displaystyle \frac{x_{2}(P)}{x_{1}(P)}}\biggr)\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right).\end{eqnarray}$$
$$\begin{eqnarray}{\displaystyle \frac{x_{2}(\unicode[STIX]{x1D70E}(P))}{x_{1}(\unicode[STIX]{x1D70E}(P))}}=\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{-2q^{2}(q-1)}\unicode[STIX]{x1D70E}\biggl({\displaystyle \frac{x_{2}(P)}{x_{1}(P)}}\biggr)\equiv \unicode[STIX]{x1D70E}\biggl({\displaystyle \frac{x_{2}(P)}{x_{1}(P)}}\biggr)\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right).\end{eqnarray}$$
Since we set
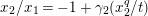 $x_{2}/x_{1}=-1+\unicode[STIX]{x1D6FE}_{2}(x_{2}^{q}/t)$
, we acquire
$x_{2}/x_{1}=-1+\unicode[STIX]{x1D6FE}_{2}(x_{2}^{q}/t)$
, we acquire
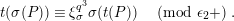 $$\begin{eqnarray}t(\unicode[STIX]{x1D70E}(P))\equiv \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{q^{3}}\unicode[STIX]{x1D70E}(t(P))\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right).\end{eqnarray}$$
$$\begin{eqnarray}t(\unicode[STIX]{x1D70E}(P))\equiv \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{q^{3}}\unicode[STIX]{x1D70E}(t(P))\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right).\end{eqnarray}$$
Therefore, we obtain
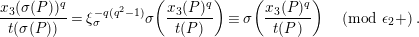 $$\begin{eqnarray}{\displaystyle \frac{x_{3}(\unicode[STIX]{x1D70E}(P))^{q}}{t(\unicode[STIX]{x1D70E}(P))}}=\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{-q(q^{2}-1)}\unicode[STIX]{x1D70E}\biggl({\displaystyle \frac{x_{3}(P)^{q}}{t(P)}}\biggr)\equiv \unicode[STIX]{x1D70E}\biggl({\displaystyle \frac{x_{3}(P)^{q}}{t(P)}}\biggr)\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right).\end{eqnarray}$$
$$\begin{eqnarray}{\displaystyle \frac{x_{3}(\unicode[STIX]{x1D70E}(P))^{q}}{t(\unicode[STIX]{x1D70E}(P))}}=\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{-q(q^{2}-1)}\unicode[STIX]{x1D70E}\biggl({\displaystyle \frac{x_{3}(P)^{q}}{t(P)}}\biggr)\equiv \unicode[STIX]{x1D70E}\biggl({\displaystyle \frac{x_{3}(P)^{q}}{t(P)}}\biggr)\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{2}+\right).\end{eqnarray}$$
Since we set
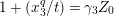 $1+(x_{3}^{q}/t)=\unicode[STIX]{x1D6FE}_{3}Z_{0}$
, we obtain
$1+(x_{3}^{q}/t)=\unicode[STIX]{x1D6FE}_{3}Z_{0}$
, we obtain
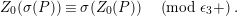 $$\begin{eqnarray}Z_{0}(\unicode[STIX]{x1D70E}(P))\equiv \unicode[STIX]{x1D70E}(Z_{0}(P))\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{3}+\right).\end{eqnarray}$$
$$\begin{eqnarray}Z_{0}(\unicode[STIX]{x1D70E}(P))\equiv \unicode[STIX]{x1D70E}(Z_{0}(P))\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{3}+\right).\end{eqnarray}$$
Therefore, we acquire
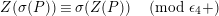 $$\begin{eqnarray}Z(\unicode[STIX]{x1D70E}(P))\equiv \unicode[STIX]{x1D70E}(Z(P))\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{4}+\right)\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D70E}(P))\equiv \unicode[STIX]{x1D70E}(Z(P))\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{4}+\right)\end{eqnarray}$$
by
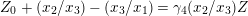 $Z_{0}+(x_{2}/x_{3})-(x_{3}/x_{1})=\unicode[STIX]{x1D6FE}_{4}(x_{2}/x_{3})Z$
.
$Z_{0}+(x_{2}/x_{3})-(x_{3}/x_{1})=\unicode[STIX]{x1D6FE}_{4}(x_{2}/x_{3})Z$
.
The assertion follows from
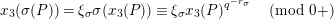 $$\begin{eqnarray}x_{3}(\unicode[STIX]{x1D70E}(P))=\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(x_{3}(P))\equiv \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}x_{3}(P)^{q^{-r_{\unicode[STIX]{x1D70E}}}}\quad \left(\text{mod}~0+\right)\end{eqnarray}$$
$$\begin{eqnarray}x_{3}(\unicode[STIX]{x1D70E}(P))=\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(x_{3}(P))\equiv \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}x_{3}(P)^{q^{-r_{\unicode[STIX]{x1D70E}}}}\quad \left(\text{mod}~0+\right)\end{eqnarray}$$
and (6.1).◻
6.2 Action of the Weil group on
 $\overline{\mathbf{X}}_{\unicode[STIX]{x1D702}}$
$\overline{\mathbf{X}}_{\unicode[STIX]{x1D702}}$
In this subsection, let
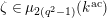 $\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})$
. Until Lemma 6.8, let
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})$
. Until Lemma 6.8, let
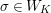 $\unicode[STIX]{x1D70E}\in W_{K}$
.
$\unicode[STIX]{x1D70E}\in W_{K}$
.
6.2.1
 $q$
odd
$q$
odd
We assume that
![]() $q$
is odd. We use the notation in Section 4.4.1. By (6.1) and
$q$
is odd. We use the notation in Section 4.4.1. By (6.1) and
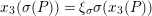 $x_{3}(\unicode[STIX]{x1D70E}(P))=\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(x_{3}(P))$
, we have
$x_{3}(\unicode[STIX]{x1D70E}(P))=\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(x_{3}(P))$
, we have
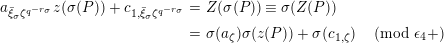 $$\begin{eqnarray}\displaystyle a_{\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}}z(\unicode[STIX]{x1D70E}(P))+c_{1,\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}} & = & \displaystyle Z(\unicode[STIX]{x1D70E}(P))\equiv \unicode[STIX]{x1D70E}(Z(P))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70E}(a_{\unicode[STIX]{x1D701}})\unicode[STIX]{x1D70E}(z(P))+\unicode[STIX]{x1D70E}(c_{1,\unicode[STIX]{x1D701}})\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{4}+\right)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}}z(\unicode[STIX]{x1D70E}(P))+c_{1,\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}} & = & \displaystyle Z(\unicode[STIX]{x1D70E}(P))\equiv \unicode[STIX]{x1D70E}(Z(P))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70E}(a_{\unicode[STIX]{x1D701}})\unicode[STIX]{x1D70E}(z(P))+\unicode[STIX]{x1D70E}(c_{1,\unicode[STIX]{x1D701}})\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{4}+\right)\end{eqnarray}$$
and
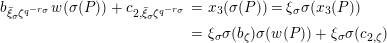 $$\begin{eqnarray}\displaystyle b_{\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}}w(\unicode[STIX]{x1D70E}(P))+c_{2,\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}} & = & \displaystyle x_{3}(\unicode[STIX]{x1D70E}(P))=\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(x_{3}(P))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(b_{\unicode[STIX]{x1D701}})\unicode[STIX]{x1D70E}(w(P))+\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(c_{2,\unicode[STIX]{x1D701}})\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle b_{\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}}w(\unicode[STIX]{x1D70E}(P))+c_{2,\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}} & = & \displaystyle x_{3}(\unicode[STIX]{x1D70E}(P))=\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(x_{3}(P))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(b_{\unicode[STIX]{x1D701}})\unicode[STIX]{x1D70E}(w(P))+\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(c_{2,\unicode[STIX]{x1D701}})\end{eqnarray}$$
for
 $P\in \mathbf{X}_{\unicode[STIX]{x1D701}}(\mathbf{C})$
. Note that
$P\in \mathbf{X}_{\unicode[STIX]{x1D701}}(\mathbf{C})$
. Note that
 $c_{1,\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}}=c_{1,\unicode[STIX]{x1D701}}$
and
$c_{1,\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}}=c_{1,\unicode[STIX]{x1D701}}$
and
 $c_{2,\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}}=\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{q^{4}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}-1}c_{2,\unicode[STIX]{x1D701}}$
. We have
$c_{2,\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}}=\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{q^{4}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}-1}c_{2,\unicode[STIX]{x1D701}}$
. We have
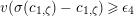 $$\begin{eqnarray}v(\unicode[STIX]{x1D70E}(c_{1,\unicode[STIX]{x1D701}})-c_{1,\unicode[STIX]{x1D701}})\geqslant \unicode[STIX]{x1D716}_{4}\end{eqnarray}$$
$$\begin{eqnarray}v(\unicode[STIX]{x1D70E}(c_{1,\unicode[STIX]{x1D701}})-c_{1,\unicode[STIX]{x1D701}})\geqslant \unicode[STIX]{x1D716}_{4}\end{eqnarray}$$
by (6.2). We put
 $$\begin{eqnarray}\begin{array}{@{}c@{}}a_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}}={\displaystyle \frac{\unicode[STIX]{x1D70E}(a_{\unicode[STIX]{x1D701}})}{\unicode[STIX]{x1D701}^{r_{\unicode[STIX]{x1D70E}}(q^{2}-1)}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{q+1}a_{\unicode[STIX]{x1D701}}}},\qquad b_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}}={\displaystyle \frac{\unicode[STIX]{x1D70E}(c_{1,\unicode[STIX]{x1D701}})-c_{1,\unicode[STIX]{x1D701}}}{\unicode[STIX]{x1D701}^{r_{\unicode[STIX]{x1D70E}}(q^{2}-1)}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{q+1}a_{\unicode[STIX]{x1D701}}}},\\ c_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}}={\displaystyle \frac{\unicode[STIX]{x1D70E}(b_{\unicode[STIX]{x1D701}})}{\unicode[STIX]{x1D701}^{(q^{-r_{\unicode[STIX]{x1D70E}}}-1)(q+3)/2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{(q+1)/2}b_{\unicode[STIX]{x1D701}}}}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}a_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}}={\displaystyle \frac{\unicode[STIX]{x1D70E}(a_{\unicode[STIX]{x1D701}})}{\unicode[STIX]{x1D701}^{r_{\unicode[STIX]{x1D70E}}(q^{2}-1)}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{q+1}a_{\unicode[STIX]{x1D701}}}},\qquad b_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}}={\displaystyle \frac{\unicode[STIX]{x1D70E}(c_{1,\unicode[STIX]{x1D701}})-c_{1,\unicode[STIX]{x1D701}}}{\unicode[STIX]{x1D701}^{r_{\unicode[STIX]{x1D70E}}(q^{2}-1)}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{q+1}a_{\unicode[STIX]{x1D701}}}},\\ c_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}}={\displaystyle \frac{\unicode[STIX]{x1D70E}(b_{\unicode[STIX]{x1D701}})}{\unicode[STIX]{x1D701}^{(q^{-r_{\unicode[STIX]{x1D70E}}}-1)(q+3)/2}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{(q+1)/2}b_{\unicode[STIX]{x1D701}}}}.\end{array}\end{eqnarray}$$
Then, we have
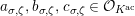 $a_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}},b_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}},c_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}}\in {\mathcal{O}}_{K^{\text{ac}}}$
. In the following, we omit the subscript
$a_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}},b_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}},c_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}}\in {\mathcal{O}}_{K^{\text{ac}}}$
. In the following, we omit the subscript
![]() $\unicode[STIX]{x1D701}$
of
$\unicode[STIX]{x1D701}$
of
![]() $a_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}}$
,
$a_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}}$
,
![]() $b_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}}$
and
$b_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}}$
and
![]() $c_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}}$
.
$c_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}}$
.
Proposition 6.4. We have
![]() $\bar{a}_{\unicode[STIX]{x1D70E}}\in k^{\times }$
,
$\bar{a}_{\unicode[STIX]{x1D70E}}\in k^{\times }$
,
![]() $\bar{b}_{\unicode[STIX]{x1D70E}}\in k$
and
$\bar{b}_{\unicode[STIX]{x1D70E}}\in k$
and
![]() $\bar{a}_{\unicode[STIX]{x1D70E}}=\bar{c}_{\unicode[STIX]{x1D70E}}^{2}$
. Further,
$\bar{a}_{\unicode[STIX]{x1D70E}}=\bar{c}_{\unicode[STIX]{x1D70E}}^{2}$
. Further,
![]() $\unicode[STIX]{x1D70E}$
induces the morphism
$\unicode[STIX]{x1D70E}$
induces the morphism
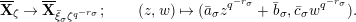 $$\begin{eqnarray}\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}\rightarrow \overline{\mathbf{X}}_{\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}};\qquad (z,w)\mapsto (\bar{a}_{\unicode[STIX]{x1D70E}}z^{q^{-r_{\unicode[STIX]{x1D70E}}}}+\bar{b}_{\unicode[STIX]{x1D70E}},\bar{c}_{\unicode[STIX]{x1D70E}}w^{q^{-r_{\unicode[STIX]{x1D70E}}}}).\end{eqnarray}$$
$$\begin{eqnarray}\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}\rightarrow \overline{\mathbf{X}}_{\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}};\qquad (z,w)\mapsto (\bar{a}_{\unicode[STIX]{x1D70E}}z^{q^{-r_{\unicode[STIX]{x1D70E}}}}+\bar{b}_{\unicode[STIX]{x1D70E}},\bar{c}_{\unicode[STIX]{x1D70E}}w^{q^{-r_{\unicode[STIX]{x1D70E}}}}).\end{eqnarray}$$
Proof. We have
 $$\begin{eqnarray}v(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(c_{2,\unicode[STIX]{x1D701}})-\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{q^{4}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}-1}c_{2,\unicode[STIX]{x1D701}})\geqslant \unicode[STIX]{x1D716}_{3}\end{eqnarray}$$
$$\begin{eqnarray}v(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(c_{2,\unicode[STIX]{x1D701}})-\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}^{q^{4}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}-1}c_{2,\unicode[STIX]{x1D701}})\geqslant \unicode[STIX]{x1D716}_{3}\end{eqnarray}$$
by
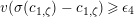 $v(\unicode[STIX]{x1D70E}(c_{1,\unicode[STIX]{x1D701}})-c_{1,\unicode[STIX]{x1D701}})\geqslant \unicode[STIX]{x1D716}_{4}$
. Hence, we have the last assertion by (6.2) and (6.3). By the definition of
$v(\unicode[STIX]{x1D70E}(c_{1,\unicode[STIX]{x1D701}})-c_{1,\unicode[STIX]{x1D701}})\geqslant \unicode[STIX]{x1D716}_{4}$
. Hence, we have the last assertion by (6.2) and (6.3). By the definition of
![]() $a_{\unicode[STIX]{x1D701}}$
,
$a_{\unicode[STIX]{x1D701}}$
,
![]() $b_{\unicode[STIX]{x1D701}}$
and
$b_{\unicode[STIX]{x1D701}}$
and
![]() $c_{1,\unicode[STIX]{x1D701}}$
, we can check that
$c_{1,\unicode[STIX]{x1D701}}$
, we can check that
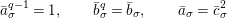 $$\begin{eqnarray}\bar{a}_{\unicode[STIX]{x1D70E}}^{q-1}=1,\qquad \bar{b}_{\unicode[STIX]{x1D70E}}^{q}=\bar{b}_{\unicode[STIX]{x1D70E}},\qquad \bar{a}_{\unicode[STIX]{x1D70E}}=\bar{c}_{\unicode[STIX]{x1D70E}}^{2}\end{eqnarray}$$
$$\begin{eqnarray}\bar{a}_{\unicode[STIX]{x1D70E}}^{q-1}=1,\qquad \bar{b}_{\unicode[STIX]{x1D70E}}^{q}=\bar{b}_{\unicode[STIX]{x1D70E}},\qquad \bar{a}_{\unicode[STIX]{x1D70E}}=\bar{c}_{\unicode[STIX]{x1D70E}}^{2}\end{eqnarray}$$
using
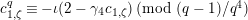 $c_{1,\unicode[STIX]{x1D701}}^{q}\equiv -\unicode[STIX]{x1D704}(2-\unicode[STIX]{x1D6FE}_{4}c_{1,\unicode[STIX]{x1D701}})\;(\text{mod}~(q-1)/q^{4})$
.◻
$c_{1,\unicode[STIX]{x1D701}}^{q}\equiv -\unicode[STIX]{x1D704}(2-\unicode[STIX]{x1D6FE}_{4}c_{1,\unicode[STIX]{x1D701}})\;(\text{mod}~(q-1)/q^{4})$
.◻
We put
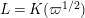 $L=K(\unicode[STIX]{x1D71B}^{1/2})$
and
$L=K(\unicode[STIX]{x1D71B}^{1/2})$
and
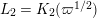 $L_{2}=K_{2}(\unicode[STIX]{x1D71B}^{1/2})$
in
$L_{2}=K_{2}(\unicode[STIX]{x1D71B}^{1/2})$
in
![]() $K^{\text{ac}}$
. Let
$K^{\text{ac}}$
. Let
![]() $\text{LT}_{L_{2}}$
be the formal
$\text{LT}_{L_{2}}$
be the formal
![]() ${\mathcal{O}}_{L_{2}}$
-module over
${\mathcal{O}}_{L_{2}}$
-module over
![]() ${\mathcal{O}}_{L^{\text{ur}}}$
of dimension
${\mathcal{O}}_{L^{\text{ur}}}$
of dimension
![]() $1$
such that
$1$
such that
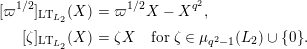 $$\begin{eqnarray}\displaystyle \text{}[\unicode[STIX]{x1D71B}^{1/2}]_{\text{LT}_{L_{2}}}(X) & = & \displaystyle \unicode[STIX]{x1D71B}^{1/2}X-X^{q^{2}},\nonumber\\ \displaystyle \text{}[\unicode[STIX]{x1D701}]_{\text{LT}_{L_{2}}}(X) & = & \displaystyle \unicode[STIX]{x1D701}X\quad \text{for }\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{q^{2}-1}(L_{2})\cup \{0\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{}[\unicode[STIX]{x1D71B}^{1/2}]_{\text{LT}_{L_{2}}}(X) & = & \displaystyle \unicode[STIX]{x1D71B}^{1/2}X-X^{q^{2}},\nonumber\\ \displaystyle \text{}[\unicode[STIX]{x1D701}]_{\text{LT}_{L_{2}}}(X) & = & \displaystyle \unicode[STIX]{x1D701}X\quad \text{for }\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{q^{2}-1}(L_{2})\cup \{0\}.\nonumber\end{eqnarray}$$
We put
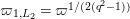 $\unicode[STIX]{x1D71B}_{1,L_{2}}=\unicode[STIX]{x1D71B}^{1/(2(q^{2}-1))}$
and take
$\unicode[STIX]{x1D71B}_{1,L_{2}}=\unicode[STIX]{x1D71B}^{1/(2(q^{2}-1))}$
and take
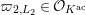 $\unicode[STIX]{x1D71B}_{2,L_{2}}\in {\mathcal{O}}_{K^{\text{ac}}}$
such that
$\unicode[STIX]{x1D71B}_{2,L_{2}}\in {\mathcal{O}}_{K^{\text{ac}}}$
such that
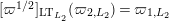 $[\unicode[STIX]{x1D71B}^{1/2}]_{\text{LT}_{L_{2}}}(\unicode[STIX]{x1D71B}_{2,L_{2}})=\unicode[STIX]{x1D71B}_{1,L_{2}}$
. Let
$[\unicode[STIX]{x1D71B}^{1/2}]_{\text{LT}_{L_{2}}}(\unicode[STIX]{x1D71B}_{2,L_{2}})=\unicode[STIX]{x1D71B}_{1,L_{2}}$
. Let
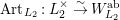 $\text{Art}_{L_{2}}:L_{2}^{\times }\stackrel{{\sim}}{\rightarrow }W_{L_{2}}^{\text{ab}}$
be the Artin reciprocity map normalized so that the image by
$\text{Art}_{L_{2}}:L_{2}^{\times }\stackrel{{\sim}}{\rightarrow }W_{L_{2}}^{\text{ab}}$
be the Artin reciprocity map normalized so that the image by
![]() $\text{Art}_{L_{2}}$
of a uniformizer is a lift of the geometric Frobenius. We consider the following homomorphism:
$\text{Art}_{L_{2}}$
of a uniformizer is a lift of the geometric Frobenius. We consider the following homomorphism:
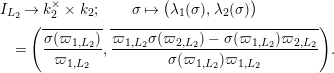 $$\begin{eqnarray}\displaystyle & & \displaystyle I_{L_{2}}\rightarrow k_{2}^{\times }\times k_{2};\qquad \unicode[STIX]{x1D70E}\mapsto (\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E}),\unicode[STIX]{x1D706}_{2}(\unicode[STIX]{x1D70E}))\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\overline{{\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}_{1,L_{2}})}{\unicode[STIX]{x1D71B}_{1,L_{2}}}}},\overline{{\displaystyle \frac{\unicode[STIX]{x1D71B}_{1,L_{2}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}_{2,L_{2}})-\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}_{1,L_{2}})\unicode[STIX]{x1D71B}_{2,L_{2}}}{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}_{1,L_{2}})\unicode[STIX]{x1D71B}_{1,L_{2}}}}}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle I_{L_{2}}\rightarrow k_{2}^{\times }\times k_{2};\qquad \unicode[STIX]{x1D70E}\mapsto (\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E}),\unicode[STIX]{x1D706}_{2}(\unicode[STIX]{x1D70E}))\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\overline{{\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}_{1,L_{2}})}{\unicode[STIX]{x1D71B}_{1,L_{2}}}}},\overline{{\displaystyle \frac{\unicode[STIX]{x1D71B}_{1,L_{2}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}_{2,L_{2}})-\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}_{1,L_{2}})\unicode[STIX]{x1D71B}_{2,L_{2}}}{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}_{1,L_{2}})\unicode[STIX]{x1D71B}_{1,L_{2}}}}}\right).\nonumber\end{eqnarray}$$
This map is equal to the composite
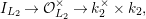 $$\begin{eqnarray}I_{L_{2}}\rightarrow {\mathcal{O}}_{L_{2}}^{\times }\rightarrow k_{2}^{\times }\times k_{2},\end{eqnarray}$$
$$\begin{eqnarray}I_{L_{2}}\rightarrow {\mathcal{O}}_{L_{2}}^{\times }\rightarrow k_{2}^{\times }\times k_{2},\end{eqnarray}$$
where the first homomorphism is induced from the inverse of
![]() $\text{Art}_{L_{2}}$
, and the second homomorphism is given by
$\text{Art}_{L_{2}}$
, and the second homomorphism is given by
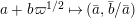 $a+b\unicode[STIX]{x1D71B}^{1/2}\mapsto (\bar{a},\bar{b}/\bar{a})$
for
$a+b\unicode[STIX]{x1D71B}^{1/2}\mapsto (\bar{a},\bar{b}/\bar{a})$
for
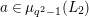 $a\in \unicode[STIX]{x1D707}_{q^{2}-1}(L_{2})$
and
$a\in \unicode[STIX]{x1D707}_{q^{2}-1}(L_{2})$
and
![]() $b\in {\mathcal{O}}_{L_{2}}$
. Then, we rewrite Proposition 6.4 as follows.
$b\in {\mathcal{O}}_{L_{2}}$
. Then, we rewrite Proposition 6.4 as follows.
Corollary 6.5. Let
![]() $\unicode[STIX]{x1D70E}\in I_{L}$
. We put
$\unicode[STIX]{x1D70E}\in I_{L}$
. We put
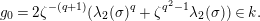 $$\begin{eqnarray}g_{0}=2\unicode[STIX]{x1D701}^{-(q+1)}(\unicode[STIX]{x1D706}_{2}(\unicode[STIX]{x1D70E})^{q}+\unicode[STIX]{x1D701}^{q^{2}-1}\unicode[STIX]{x1D706}_{2}(\unicode[STIX]{x1D70E}))\in k.\end{eqnarray}$$
$$\begin{eqnarray}g_{0}=2\unicode[STIX]{x1D701}^{-(q+1)}(\unicode[STIX]{x1D706}_{2}(\unicode[STIX]{x1D70E})^{q}+\unicode[STIX]{x1D701}^{q^{2}-1}\unicode[STIX]{x1D706}_{2}(\unicode[STIX]{x1D70E}))\in k.\end{eqnarray}$$
Then,
![]() $\unicode[STIX]{x1D70E}$
induces the morphism
$\unicode[STIX]{x1D70E}$
induces the morphism
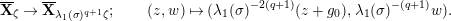 $$\begin{eqnarray}\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}\rightarrow \overline{\mathbf{X}}_{\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{q+1}\unicode[STIX]{x1D701}};\qquad (z,w)\mapsto (\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{-2(q+1)}(z+g_{0}),\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{-(q+1)}w).\end{eqnarray}$$
$$\begin{eqnarray}\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}\rightarrow \overline{\mathbf{X}}_{\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{q+1}\unicode[STIX]{x1D701}};\qquad (z,w)\mapsto (\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{-2(q+1)}(z+g_{0}),\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{-(q+1)}w).\end{eqnarray}$$
Proof. We can check that
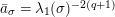 $\bar{a}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{-2(q+1)}$
and
$\bar{a}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{-2(q+1)}$
and
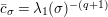 $\bar{c}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{-(q+1)}$
easily. We prove that
$\bar{c}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{-(q+1)}$
easily. We prove that
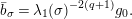 $$\begin{eqnarray}\bar{b}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{-2(q+1)}g_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\bar{b}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{-2(q+1)}g_{0}.\end{eqnarray}$$
We simply write
![]() $\unicode[STIX]{x1D71B}_{i}$
for
$\unicode[STIX]{x1D71B}_{i}$
for
![]() $\unicode[STIX]{x1D71B}_{i,L_{2}}$
. We put
$\unicode[STIX]{x1D71B}_{i,L_{2}}$
. We put
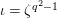 $\unicode[STIX]{x1D704}=\unicode[STIX]{x1D701}^{q^{2}-1}$
and
$\unicode[STIX]{x1D704}=\unicode[STIX]{x1D701}^{q^{2}-1}$
and
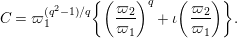 $$\begin{eqnarray}C=\unicode[STIX]{x1D71B}_{1}^{(q^{2}-1)/q}\biggl\{\biggl({\displaystyle \frac{\unicode[STIX]{x1D71B}_{2}}{\unicode[STIX]{x1D71B}_{1}}}\biggr)^{q}+\unicode[STIX]{x1D704}\biggl({\displaystyle \frac{\unicode[STIX]{x1D71B}_{2}}{\unicode[STIX]{x1D71B}_{1}}}\biggr)\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}C=\unicode[STIX]{x1D71B}_{1}^{(q^{2}-1)/q}\biggl\{\biggl({\displaystyle \frac{\unicode[STIX]{x1D71B}_{2}}{\unicode[STIX]{x1D71B}_{1}}}\biggr)^{q}+\unicode[STIX]{x1D704}\biggl({\displaystyle \frac{\unicode[STIX]{x1D71B}_{2}}{\unicode[STIX]{x1D71B}_{1}}}\biggr)\biggr\}.\end{eqnarray}$$
Then, we have
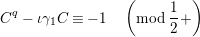 $$\begin{eqnarray}C^{q}-\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FE}_{1}C\equiv -1\quad \left(\text{mod}\,{\displaystyle \frac{1}{2}}+\right)\end{eqnarray}$$
$$\begin{eqnarray}C^{q}-\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FE}_{1}C\equiv -1\quad \left(\text{mod}\,{\displaystyle \frac{1}{2}}+\right)\end{eqnarray}$$
by
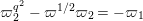 $\unicode[STIX]{x1D71B}_{2}^{q^{2}}-\unicode[STIX]{x1D71B}^{1/2}\unicode[STIX]{x1D71B}_{2}=-\unicode[STIX]{x1D71B}_{1}$
. We can easily check the equality
$\unicode[STIX]{x1D71B}_{2}^{q^{2}}-\unicode[STIX]{x1D71B}^{1/2}\unicode[STIX]{x1D71B}_{2}=-\unicode[STIX]{x1D71B}_{1}$
. We can easily check the equality
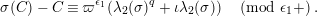 $$\begin{eqnarray}\unicode[STIX]{x1D70E}(C)-C\equiv \unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{1}}(\unicode[STIX]{x1D706}_{2}(\unicode[STIX]{x1D70E})^{q}+\unicode[STIX]{x1D704}\unicode[STIX]{x1D706}_{2}(\unicode[STIX]{x1D70E}))\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}(C)-C\equiv \unicode[STIX]{x1D71B}^{\unicode[STIX]{x1D716}_{1}}(\unicode[STIX]{x1D706}_{2}(\unicode[STIX]{x1D70E})^{q}+\unicode[STIX]{x1D704}\unicode[STIX]{x1D706}_{2}(\unicode[STIX]{x1D70E}))\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right).\end{eqnarray}$$
On the other hand, we can check
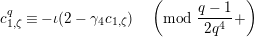 $$\begin{eqnarray}c_{1,\unicode[STIX]{x1D701}}^{q}\equiv -\unicode[STIX]{x1D704}(2-\unicode[STIX]{x1D6FE}_{4}c_{1,\unicode[STIX]{x1D701}})\quad \left(\text{mod}~{\displaystyle \frac{q-1}{2q^{4}}}+\right)\end{eqnarray}$$
$$\begin{eqnarray}c_{1,\unicode[STIX]{x1D701}}^{q}\equiv -\unicode[STIX]{x1D704}(2-\unicode[STIX]{x1D6FE}_{4}c_{1,\unicode[STIX]{x1D701}})\quad \left(\text{mod}~{\displaystyle \frac{q-1}{2q^{4}}}+\right)\end{eqnarray}$$
by the definition of
![]() $c_{1,\unicode[STIX]{x1D701}}$
. Therefore, the elements
$c_{1,\unicode[STIX]{x1D701}}$
. Therefore, the elements
![]() $C$
and
$C$
and
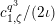 $c_{1,\unicode[STIX]{x1D701}}^{q^{3}}/(2\unicode[STIX]{x1D704})$
satisfy
$c_{1,\unicode[STIX]{x1D701}}^{q^{3}}/(2\unicode[STIX]{x1D704})$
satisfy
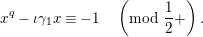 $$\begin{eqnarray}x^{q}-\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FE}_{1}x\equiv -1\quad \left(\text{mod}~{\displaystyle \frac{1}{2}}+\right).\end{eqnarray}$$
$$\begin{eqnarray}x^{q}-\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FE}_{1}x\equiv -1\quad \left(\text{mod}~{\displaystyle \frac{1}{2}}+\right).\end{eqnarray}$$
Hence, we obtain
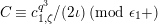 $C\equiv c_{1,\unicode[STIX]{x1D701}}^{q^{3}}/(2\unicode[STIX]{x1D704})\;(\text{mod}~\unicode[STIX]{x1D716}_{1}+)$
. This implies that
$C\equiv c_{1,\unicode[STIX]{x1D701}}^{q^{3}}/(2\unicode[STIX]{x1D704})\;(\text{mod}~\unicode[STIX]{x1D716}_{1}+)$
. This implies that
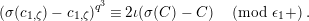 $$\begin{eqnarray}(\unicode[STIX]{x1D70E}(c_{1,\unicode[STIX]{x1D701}})-c_{1,\unicode[STIX]{x1D701}})^{q^{3}}\equiv 2\unicode[STIX]{x1D704}(\unicode[STIX]{x1D70E}(C)-C)\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70E}(c_{1,\unicode[STIX]{x1D701}})-c_{1,\unicode[STIX]{x1D701}})^{q^{3}}\equiv 2\unicode[STIX]{x1D704}(\unicode[STIX]{x1D70E}(C)-C)\quad \left(\text{mod}~\unicode[STIX]{x1D716}_{1}+\right).\end{eqnarray}$$
Therefore, we obtain
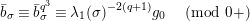 $$\begin{eqnarray}\bar{b}_{\unicode[STIX]{x1D70E}}\equiv \bar{b}_{\unicode[STIX]{x1D70E}}^{q^{3}}\equiv \unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{-2(q+1)}g_{0}\quad \left(\text{mod}~0+\right)\end{eqnarray}$$
$$\begin{eqnarray}\bar{b}_{\unicode[STIX]{x1D70E}}\equiv \bar{b}_{\unicode[STIX]{x1D70E}}^{q^{3}}\equiv \unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{-2(q+1)}g_{0}\quad \left(\text{mod}~0+\right)\end{eqnarray}$$
by
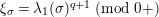 $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{q+1}\;(\text{mod}~0+)$
.◻
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D706}_{1}(\unicode[STIX]{x1D70E})^{q+1}\;(\text{mod}~0+)$
.◻
6.2.2
 $q$
even
$q$
even
We assume that
![]() $q$
is even. We use the notation in Section 4.4.2. For
$q$
is even. We use the notation in Section 4.4.2. For
 $P\in \mathbf{P}^{0}(\mathbf{C})$
, we have
$P\in \mathbf{P}^{0}(\mathbf{C})$
, we have
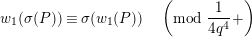 $$\begin{eqnarray}w_{1}(\unicode[STIX]{x1D70E}(P))\equiv \unicode[STIX]{x1D70E}(w_{1}(P))\quad \left(\text{mod}~{\displaystyle \frac{1}{4q^{4}}}+\right)\end{eqnarray}$$
$$\begin{eqnarray}w_{1}(\unicode[STIX]{x1D70E}(P))\equiv \unicode[STIX]{x1D70E}(w_{1}(P))\quad \left(\text{mod}~{\displaystyle \frac{1}{4q^{4}}}+\right)\end{eqnarray}$$
by (6.1). We can see that
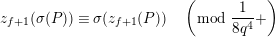 $$\begin{eqnarray}z_{f+1}(\unicode[STIX]{x1D70E}(P))\equiv \unicode[STIX]{x1D70E}(z_{f+1}(P))\quad \left(\text{mod}~{\displaystyle \frac{1}{8q^{4}}}+\right)\end{eqnarray}$$
$$\begin{eqnarray}z_{f+1}(\unicode[STIX]{x1D70E}(P))\equiv \unicode[STIX]{x1D70E}(z_{f+1}(P))\quad \left(\text{mod}~{\displaystyle \frac{1}{8q^{4}}}+\right)\end{eqnarray}$$
Lemma 6.6. The element
![]() $\unicode[STIX]{x1D70E}$
induces the morphism
$\unicode[STIX]{x1D70E}$
induces the morphism
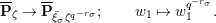 $$\begin{eqnarray}\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}\rightarrow \overline{\mathbf{P}}_{\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}};\qquad w_{1}\mapsto w_{1}^{q^{-r_{\unicode[STIX]{x1D70E}}}}.\end{eqnarray}$$
$$\begin{eqnarray}\overline{\mathbf{P}}_{\unicode[STIX]{x1D701}}\rightarrow \overline{\mathbf{P}}_{\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}}};\qquad w_{1}\mapsto w_{1}^{q^{-r_{\unicode[STIX]{x1D70E}}}}.\end{eqnarray}$$
We take
![]() $\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
. By (6.4) and (6.5), we have
$\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
. By (6.4) and (6.5), we have
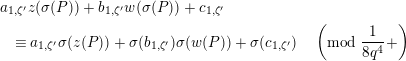 $$\begin{eqnarray}\displaystyle & & \displaystyle a_{1,\unicode[STIX]{x1D701}^{\prime }}z(\unicode[STIX]{x1D70E}(P))+b_{1,\unicode[STIX]{x1D701}^{\prime }}w(\unicode[STIX]{x1D70E}(P))+c_{1,\unicode[STIX]{x1D701}^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \equiv a_{1,\unicode[STIX]{x1D701}^{\prime }}\unicode[STIX]{x1D70E}(z(P))+\unicode[STIX]{x1D70E}(b_{1,\unicode[STIX]{x1D701}^{\prime }})\unicode[STIX]{x1D70E}(w(P))+\unicode[STIX]{x1D70E}(c_{1,\unicode[STIX]{x1D701}^{\prime }})\quad \left(\text{mod}~{\displaystyle \frac{1}{8q^{4}}}+\right)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle a_{1,\unicode[STIX]{x1D701}^{\prime }}z(\unicode[STIX]{x1D70E}(P))+b_{1,\unicode[STIX]{x1D701}^{\prime }}w(\unicode[STIX]{x1D70E}(P))+c_{1,\unicode[STIX]{x1D701}^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \equiv a_{1,\unicode[STIX]{x1D701}^{\prime }}\unicode[STIX]{x1D70E}(z(P))+\unicode[STIX]{x1D70E}(b_{1,\unicode[STIX]{x1D701}^{\prime }})\unicode[STIX]{x1D70E}(w(P))+\unicode[STIX]{x1D70E}(c_{1,\unicode[STIX]{x1D701}^{\prime }})\quad \left(\text{mod}~{\displaystyle \frac{1}{8q^{4}}}+\right)\end{eqnarray}$$
and
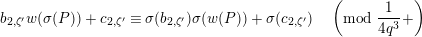 $$\begin{eqnarray}b_{2,\unicode[STIX]{x1D701}^{\prime }}w(\unicode[STIX]{x1D70E}(P))+c_{2,\unicode[STIX]{x1D701}^{\prime }}\equiv \unicode[STIX]{x1D70E}(b_{2,\unicode[STIX]{x1D701}^{\prime }})\unicode[STIX]{x1D70E}(w(P))+\unicode[STIX]{x1D70E}(c_{2,\unicode[STIX]{x1D701}^{\prime }})\quad \left(\text{mod}~{\displaystyle \frac{1}{4q^{3}}}+\right)\end{eqnarray}$$
$$\begin{eqnarray}b_{2,\unicode[STIX]{x1D701}^{\prime }}w(\unicode[STIX]{x1D70E}(P))+c_{2,\unicode[STIX]{x1D701}^{\prime }}\equiv \unicode[STIX]{x1D70E}(b_{2,\unicode[STIX]{x1D701}^{\prime }})\unicode[STIX]{x1D70E}(w(P))+\unicode[STIX]{x1D70E}(c_{2,\unicode[STIX]{x1D701}^{\prime }})\quad \left(\text{mod}~{\displaystyle \frac{1}{4q^{3}}}+\right)\end{eqnarray}$$
using
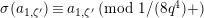 $\unicode[STIX]{x1D70E}(a_{1,\unicode[STIX]{x1D701}^{\prime }})\equiv a_{1,\unicode[STIX]{x1D701}^{\prime }}\;(\text{mod}~1/(8q^{4})+)$
. We put
$\unicode[STIX]{x1D70E}(a_{1,\unicode[STIX]{x1D701}^{\prime }})\equiv a_{1,\unicode[STIX]{x1D701}^{\prime }}\;(\text{mod}~1/(8q^{4})+)$
. We put
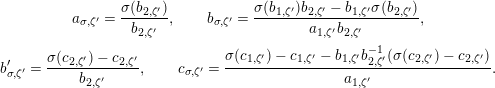 $$\begin{eqnarray}\displaystyle & \displaystyle a_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}={\displaystyle \frac{\unicode[STIX]{x1D70E}(b_{2,\unicode[STIX]{x1D701}^{\prime }})}{b_{2,\unicode[STIX]{x1D701}^{\prime }}}},\qquad b_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}={\displaystyle \frac{\unicode[STIX]{x1D70E}(b_{1,\unicode[STIX]{x1D701}^{\prime }})b_{2,\unicode[STIX]{x1D701}^{\prime }}-b_{1,\unicode[STIX]{x1D701}^{\prime }}\unicode[STIX]{x1D70E}(b_{2,\unicode[STIX]{x1D701}^{\prime }})}{a_{1,\unicode[STIX]{x1D701}^{\prime }}b_{2,\unicode[STIX]{x1D701}^{\prime }}}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}^{\prime }={\displaystyle \frac{\unicode[STIX]{x1D70E}(c_{2,\unicode[STIX]{x1D701}^{\prime }})-c_{2,\unicode[STIX]{x1D701}^{\prime }}}{b_{2,\unicode[STIX]{x1D701}^{\prime }}}},\qquad c_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}={\displaystyle \frac{\unicode[STIX]{x1D70E}(c_{1,\unicode[STIX]{x1D701}^{\prime }})-c_{1,\unicode[STIX]{x1D701}^{\prime }}-b_{1,\unicode[STIX]{x1D701}^{\prime }}b_{2,\unicode[STIX]{x1D701}^{\prime }}^{-1}(\unicode[STIX]{x1D70E}(c_{2,\unicode[STIX]{x1D701}^{\prime }})-c_{2,\unicode[STIX]{x1D701}^{\prime }})}{a_{1,\unicode[STIX]{x1D701}^{\prime }}}}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle a_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}={\displaystyle \frac{\unicode[STIX]{x1D70E}(b_{2,\unicode[STIX]{x1D701}^{\prime }})}{b_{2,\unicode[STIX]{x1D701}^{\prime }}}},\qquad b_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}={\displaystyle \frac{\unicode[STIX]{x1D70E}(b_{1,\unicode[STIX]{x1D701}^{\prime }})b_{2,\unicode[STIX]{x1D701}^{\prime }}-b_{1,\unicode[STIX]{x1D701}^{\prime }}\unicode[STIX]{x1D70E}(b_{2,\unicode[STIX]{x1D701}^{\prime }})}{a_{1,\unicode[STIX]{x1D701}^{\prime }}b_{2,\unicode[STIX]{x1D701}^{\prime }}}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}^{\prime }={\displaystyle \frac{\unicode[STIX]{x1D70E}(c_{2,\unicode[STIX]{x1D701}^{\prime }})-c_{2,\unicode[STIX]{x1D701}^{\prime }}}{b_{2,\unicode[STIX]{x1D701}^{\prime }}}},\qquad c_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}={\displaystyle \frac{\unicode[STIX]{x1D70E}(c_{1,\unicode[STIX]{x1D701}^{\prime }})-c_{1,\unicode[STIX]{x1D701}^{\prime }}-b_{1,\unicode[STIX]{x1D701}^{\prime }}b_{2,\unicode[STIX]{x1D701}^{\prime }}^{-1}(\unicode[STIX]{x1D70E}(c_{2,\unicode[STIX]{x1D701}^{\prime }})-c_{2,\unicode[STIX]{x1D701}^{\prime }})}{a_{1,\unicode[STIX]{x1D701}^{\prime }}}}. & \displaystyle \nonumber\end{eqnarray}$$
In the following, we omit the subscript
![]() $\unicode[STIX]{x1D701}^{\prime }$
of
$\unicode[STIX]{x1D701}^{\prime }$
of
![]() $a_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}$
,
$a_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}$
,
![]() $b_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}$
,
$b_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}$
,
![]() $b_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}^{\prime }$
and
$b_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}^{\prime }$
and
![]() $c_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}$
. We note that
$c_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D701}^{\prime }}$
. We note that
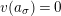 $v(a_{\unicode[STIX]{x1D70E}})=0$
. We have
$v(a_{\unicode[STIX]{x1D70E}})=0$
. We have
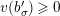 $v(b_{\unicode[STIX]{x1D70E}}^{\prime })\geqslant 0$
by (6.7). This implies that
$v(b_{\unicode[STIX]{x1D70E}}^{\prime })\geqslant 0$
by (6.7). This implies that
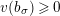 $v(b_{\unicode[STIX]{x1D70E}})\geqslant 0$
. By (6.6) and (6.7), we obtain
$v(b_{\unicode[STIX]{x1D70E}})\geqslant 0$
. By (6.6) and (6.7), we obtain
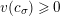 $v(c_{\unicode[STIX]{x1D70E}})\geqslant 0$
using
$v(c_{\unicode[STIX]{x1D70E}})\geqslant 0$
using
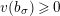 $v(b_{\unicode[STIX]{x1D70E}})\geqslant 0$
.
$v(b_{\unicode[STIX]{x1D70E}})\geqslant 0$
.
Proposition 6.7. The element
![]() $\unicode[STIX]{x1D70E}$
induces the morphism
$\unicode[STIX]{x1D70E}$
induces the morphism
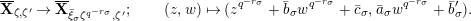 $$\begin{eqnarray}\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}\rightarrow \overline{\mathbf{X}}_{\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}},\unicode[STIX]{x1D701}^{\prime }};\qquad (z,w)\mapsto (z^{q^{-r_{\unicode[STIX]{x1D70E}}}}+\bar{b}_{\unicode[STIX]{x1D70E}}w^{q^{-r_{\unicode[STIX]{x1D70E}}}}+\bar{c}_{\unicode[STIX]{x1D70E}},\bar{a}_{\unicode[STIX]{x1D70E}}w^{q^{-r_{\unicode[STIX]{x1D70E}}}}+\bar{b}_{\unicode[STIX]{x1D70E}}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}\rightarrow \overline{\mathbf{X}}_{\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}},\unicode[STIX]{x1D701}^{\prime }};\qquad (z,w)\mapsto (z^{q^{-r_{\unicode[STIX]{x1D70E}}}}+\bar{b}_{\unicode[STIX]{x1D70E}}w^{q^{-r_{\unicode[STIX]{x1D70E}}}}+\bar{c}_{\unicode[STIX]{x1D70E}},\bar{a}_{\unicode[STIX]{x1D70E}}w^{q^{-r_{\unicode[STIX]{x1D70E}}}}+\bar{b}_{\unicode[STIX]{x1D70E}}^{\prime }).\end{eqnarray}$$
In the following, we simplify the description of
![]() $\bar{a}_{\unicode[STIX]{x1D70E}}$
,
$\bar{a}_{\unicode[STIX]{x1D70E}}$
,
![]() $\bar{b}_{\unicode[STIX]{x1D70E}}$
,
$\bar{b}_{\unicode[STIX]{x1D70E}}$
,
![]() $\bar{b}_{\unicode[STIX]{x1D70E}}^{\prime }$
and
$\bar{b}_{\unicode[STIX]{x1D70E}}^{\prime }$
and
![]() $\bar{c}_{\unicode[STIX]{x1D70E}}$
. Let
$\bar{c}_{\unicode[STIX]{x1D70E}}$
. Let
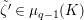 $\tilde{\unicode[STIX]{x1D701}}^{\prime }\in \unicode[STIX]{x1D707}_{q-1}(K)$
be the lift of
$\tilde{\unicode[STIX]{x1D701}}^{\prime }\in \unicode[STIX]{x1D707}_{q-1}(K)$
be the lift of
![]() $\unicode[STIX]{x1D701}^{\prime }$
. We put
$\unicode[STIX]{x1D701}^{\prime }$
. We put
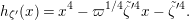 $$\begin{eqnarray}h_{\unicode[STIX]{x1D701}^{\prime }}(x)=x^{4}-\unicode[STIX]{x1D71B}^{1/4}\tilde{\unicode[STIX]{x1D701}}^{\prime 4}x-\tilde{\unicode[STIX]{x1D701}}^{\prime 4}.\end{eqnarray}$$
$$\begin{eqnarray}h_{\unicode[STIX]{x1D701}^{\prime }}(x)=x^{4}-\unicode[STIX]{x1D71B}^{1/4}\tilde{\unicode[STIX]{x1D701}}^{\prime 4}x-\tilde{\unicode[STIX]{x1D701}}^{\prime 4}.\end{eqnarray}$$
Lemma 6.8. There is a root
![]() $\unicode[STIX]{x1D6FF}_{1}$
of
$\unicode[STIX]{x1D6FF}_{1}$
of
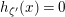 $h_{\unicode[STIX]{x1D701}^{\prime }}(x)=0$
such that
$h_{\unicode[STIX]{x1D701}^{\prime }}(x)=0$
such that
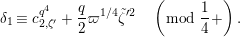 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{1}\equiv c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}}+{\displaystyle \frac{q}{2}}\unicode[STIX]{x1D71B}^{1/4}\tilde{\unicode[STIX]{x1D701}}^{\prime 2}\quad \left(\text{mod}~{\displaystyle \frac{1}{4}}+\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{1}\equiv c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}}+{\displaystyle \frac{q}{2}}\unicode[STIX]{x1D71B}^{1/4}\tilde{\unicode[STIX]{x1D701}}^{\prime 2}\quad \left(\text{mod}~{\displaystyle \frac{1}{4}}+\right).\end{eqnarray}$$
Proof. We put
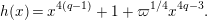 $$\begin{eqnarray}h(x)=x^{4(q-1)}+1+\unicode[STIX]{x1D71B}^{1/4}x^{4q-3}.\end{eqnarray}$$
$$\begin{eqnarray}h(x)=x^{4(q-1)}+1+\unicode[STIX]{x1D71B}^{1/4}x^{4q-3}.\end{eqnarray}$$
By the definition of
![]() $c_{2,\unicode[STIX]{x1D701}^{\prime }}$
, we have
$c_{2,\unicode[STIX]{x1D701}^{\prime }}$
, we have
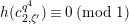 $h(c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}})\equiv 0\;(\text{mod}~1)$
. Hence, we have a root
$h(c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}})\equiv 0\;(\text{mod}~1)$
. Hence, we have a root
![]() $c_{2}^{\prime }$
of
$c_{2}^{\prime }$
of
![]() $h$
such that
$h$
such that
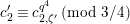 $c_{2}^{\prime }\equiv c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}}\;(\text{mod}~3/4)$
by Newton’s method. We can check that
$c_{2}^{\prime }\equiv c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}}\;(\text{mod}~3/4)$
by Newton’s method. We can check that
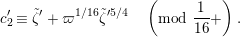 $$\begin{eqnarray}c_{2}^{\prime }\equiv \tilde{\unicode[STIX]{x1D701}}^{\prime }+\unicode[STIX]{x1D71B}^{1/16}\tilde{\unicode[STIX]{x1D701}}^{\prime 5/4}\quad \left(\text{mod}~{\displaystyle \frac{1}{16}}+\right).\end{eqnarray}$$
$$\begin{eqnarray}c_{2}^{\prime }\equiv \tilde{\unicode[STIX]{x1D701}}^{\prime }+\unicode[STIX]{x1D71B}^{1/16}\tilde{\unicode[STIX]{x1D701}}^{\prime 5/4}\quad \left(\text{mod}~{\displaystyle \frac{1}{16}}+\right).\end{eqnarray}$$
We define a parameter
![]() $s$
with
$s$
with
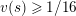 $v(s)\geqslant 1/16$
by
$v(s)\geqslant 1/16$
by
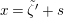 $x=\tilde{\unicode[STIX]{x1D701}}^{\prime }+s$
. Then, we have
$x=\tilde{\unicode[STIX]{x1D701}}^{\prime }+s$
. Then, we have
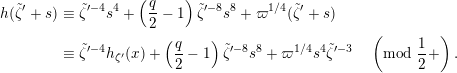 $$\begin{eqnarray}\displaystyle h(\tilde{\unicode[STIX]{x1D701}}^{\prime }+s) & \equiv & \displaystyle \tilde{\unicode[STIX]{x1D701}}^{\prime -4}s^{4}+\left(\frac{q}{2}-1\right)\tilde{\unicode[STIX]{x1D701}}^{\prime -8}s^{8}+\unicode[STIX]{x1D71B}^{1/4}(\tilde{\unicode[STIX]{x1D701}}^{\prime }+s)\nonumber\\ \displaystyle & \equiv & \displaystyle \tilde{\unicode[STIX]{x1D701}}^{\prime -4}h_{\unicode[STIX]{x1D701}^{\prime }}(x)+\left({\displaystyle \frac{q}{2}}-1\right)\tilde{\unicode[STIX]{x1D701}}^{\prime -8}s^{8}+\unicode[STIX]{x1D71B}^{1/4}s^{4}\tilde{\unicode[STIX]{x1D701}}^{\prime -3}\quad \left(\text{mod}~{\displaystyle \frac{1}{2}}+\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle h(\tilde{\unicode[STIX]{x1D701}}^{\prime }+s) & \equiv & \displaystyle \tilde{\unicode[STIX]{x1D701}}^{\prime -4}s^{4}+\left(\frac{q}{2}-1\right)\tilde{\unicode[STIX]{x1D701}}^{\prime -8}s^{8}+\unicode[STIX]{x1D71B}^{1/4}(\tilde{\unicode[STIX]{x1D701}}^{\prime }+s)\nonumber\\ \displaystyle & \equiv & \displaystyle \tilde{\unicode[STIX]{x1D701}}^{\prime -4}h_{\unicode[STIX]{x1D701}^{\prime }}(x)+\left({\displaystyle \frac{q}{2}}-1\right)\tilde{\unicode[STIX]{x1D701}}^{\prime -8}s^{8}+\unicode[STIX]{x1D71B}^{1/4}s^{4}\tilde{\unicode[STIX]{x1D701}}^{\prime -3}\quad \left(\text{mod}~{\displaystyle \frac{1}{2}}+\right).\nonumber\end{eqnarray}$$
This implies that
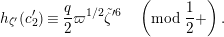 $$\begin{eqnarray}h_{\unicode[STIX]{x1D701}^{\prime }}(c_{2}^{\prime })\equiv {\displaystyle \frac{q}{2}}\unicode[STIX]{x1D71B}^{1/2}\tilde{\unicode[STIX]{x1D701}}^{\prime 6}\quad \left(\text{mod}\,{\displaystyle \frac{1}{2}}+\right).\end{eqnarray}$$
$$\begin{eqnarray}h_{\unicode[STIX]{x1D701}^{\prime }}(c_{2}^{\prime })\equiv {\displaystyle \frac{q}{2}}\unicode[STIX]{x1D71B}^{1/2}\tilde{\unicode[STIX]{x1D701}}^{\prime 6}\quad \left(\text{mod}\,{\displaystyle \frac{1}{2}}+\right).\end{eqnarray}$$
Therefore, we have a root
![]() $\unicode[STIX]{x1D6FF}_{1}$
of
$\unicode[STIX]{x1D6FF}_{1}$
of
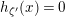 $h_{\unicode[STIX]{x1D701}^{\prime }}(x)=0$
such that
$h_{\unicode[STIX]{x1D701}^{\prime }}(x)=0$
such that
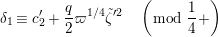 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{1}\equiv c_{2}^{\prime }+{\displaystyle \frac{q}{2}}\unicode[STIX]{x1D71B}^{1/4}\tilde{\unicode[STIX]{x1D701}}^{\prime 2}\quad \left(\text{mod}~{\displaystyle \frac{1}{4}}+\right)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{1}\equiv c_{2}^{\prime }+{\displaystyle \frac{q}{2}}\unicode[STIX]{x1D71B}^{1/4}\tilde{\unicode[STIX]{x1D701}}^{\prime 2}\quad \left(\text{mod}~{\displaystyle \frac{1}{4}}+\right)\end{eqnarray}$$
by Newton’s method. ◻
By the definition of
![]() $b_{2,\unicode[STIX]{x1D701}^{\prime }}$
, we have
$b_{2,\unicode[STIX]{x1D701}^{\prime }}$
, we have
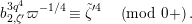 $$\begin{eqnarray}b_{2,\unicode[STIX]{x1D701}^{\prime }}^{3q^{4}}\unicode[STIX]{x1D71B}^{-1/4}\equiv \tilde{\unicode[STIX]{x1D701}}^{\prime 4}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
$$\begin{eqnarray}b_{2,\unicode[STIX]{x1D701}^{\prime }}^{3q^{4}}\unicode[STIX]{x1D71B}^{-1/4}\equiv \tilde{\unicode[STIX]{x1D701}}^{\prime 4}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D701}^{\prime \prime }$
be the element of
$\unicode[STIX]{x1D701}^{\prime \prime }$
be the element of
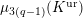 $\unicode[STIX]{x1D707}_{3(q-1)}(K^{\text{ur}})$
satisfying
$\unicode[STIX]{x1D707}_{3(q-1)}(K^{\text{ur}})$
satisfying
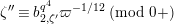 $\unicode[STIX]{x1D701}^{\prime \prime }\equiv b_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}}\unicode[STIX]{x1D71B}^{-1/12}\;(\text{mod}~0+)$
. Note that
$\unicode[STIX]{x1D701}^{\prime \prime }\equiv b_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}}\unicode[STIX]{x1D71B}^{-1/12}\;(\text{mod}~0+)$
. Note that
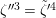 $\unicode[STIX]{x1D701}^{\prime \prime 3}=\tilde{\unicode[STIX]{x1D701}}^{\prime 4}$
. We take
$\unicode[STIX]{x1D701}^{\prime \prime 3}=\tilde{\unicode[STIX]{x1D701}}^{\prime 4}$
. We take
![]() $\unicode[STIX]{x1D6FF}_{1}$
as in Lemma 6.8 and put
$\unicode[STIX]{x1D6FF}_{1}$
as in Lemma 6.8 and put
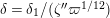 $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{1}/(\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12})$
. Then, we have
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{1}/(\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12})$
. Then, we have
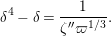 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}^{4}-\unicode[STIX]{x1D6FF}={\displaystyle \frac{1}{\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3}}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}^{4}-\unicode[STIX]{x1D6FF}={\displaystyle \frac{1}{\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3}}}.\end{eqnarray}$$
Note that
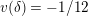 $v(\unicode[STIX]{x1D6FF})=-1/12$
. We take
$v(\unicode[STIX]{x1D6FF})=-1/12$
. We take
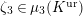 $\unicode[STIX]{x1D701}_{3}\in \unicode[STIX]{x1D707}_{3}(K^{\text{ur}})$
such that
$\unicode[STIX]{x1D701}_{3}\in \unicode[STIX]{x1D707}_{3}(K^{\text{ur}})$
such that
![]() $\unicode[STIX]{x1D701}_{3}\neq 1$
, and put
$\unicode[STIX]{x1D701}_{3}\neq 1$
, and put
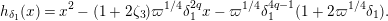 $$\begin{eqnarray}h_{\unicode[STIX]{x1D6FF}_{1}}(x)=x^{2}-(1+2\unicode[STIX]{x1D701}_{3})\unicode[STIX]{x1D71B}^{1/4}\unicode[STIX]{x1D6FF}_{1}^{2q}x-\unicode[STIX]{x1D71B}^{1/4}\unicode[STIX]{x1D6FF}_{1}^{4q-1}(1+2\unicode[STIX]{x1D71B}^{1/4}\unicode[STIX]{x1D6FF}_{1}).\end{eqnarray}$$
$$\begin{eqnarray}h_{\unicode[STIX]{x1D6FF}_{1}}(x)=x^{2}-(1+2\unicode[STIX]{x1D701}_{3})\unicode[STIX]{x1D71B}^{1/4}\unicode[STIX]{x1D6FF}_{1}^{2q}x-\unicode[STIX]{x1D71B}^{1/4}\unicode[STIX]{x1D6FF}_{1}^{4q-1}(1+2\unicode[STIX]{x1D71B}^{1/4}\unicode[STIX]{x1D6FF}_{1}).\end{eqnarray}$$
Lemma 6.9. There is a root
![]() $\unicode[STIX]{x1D703}_{1}$
of
$\unicode[STIX]{x1D703}_{1}$
of
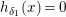 $h_{\unicode[STIX]{x1D6FF}_{1}}(x)=0$
such that
$h_{\unicode[STIX]{x1D6FF}_{1}}(x)=0$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{1}\equiv c_{1,\unicode[STIX]{x1D701}^{\prime }}^{2q^{4}}\quad \left(\text{mod}~\frac{1}{4}+\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{1}\equiv c_{1,\unicode[STIX]{x1D701}^{\prime }}^{2q^{4}}\quad \left(\text{mod}~\frac{1}{4}+\right).\end{eqnarray}$$
Proof. By the definition of
![]() $c_{1,\unicode[STIX]{x1D701}^{\prime }}$
and
$c_{1,\unicode[STIX]{x1D701}^{\prime }}$
and
![]() $c_{2,\unicode[STIX]{x1D701}^{\prime }}$
, we have
$c_{2,\unicode[STIX]{x1D701}^{\prime }}$
, we have
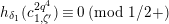 $h_{\unicode[STIX]{x1D6FF}_{1}}(c_{1,\unicode[STIX]{x1D701}^{\prime }}^{2q^{4}})\equiv 0\;(\text{mod}~1/2+)$
. Hence, we can show the claim using Newton’s method.◻
$h_{\unicode[STIX]{x1D6FF}_{1}}(c_{1,\unicode[STIX]{x1D701}^{\prime }}^{2q^{4}})\equiv 0\;(\text{mod}~1/2+)$
. Hence, we can show the claim using Newton’s method.◻
We take
![]() $\unicode[STIX]{x1D703}_{1}$
as in Lemma 6.9 and put
$\unicode[STIX]{x1D703}_{1}$
as in Lemma 6.9 and put
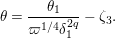 $$\begin{eqnarray}\unicode[STIX]{x1D703}={\displaystyle \frac{\unicode[STIX]{x1D703}_{1}}{\unicode[STIX]{x1D71B}^{1/4}\unicode[STIX]{x1D6FF}_{1}^{2q}}}-\unicode[STIX]{x1D701}_{3}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}={\displaystyle \frac{\unicode[STIX]{x1D703}_{1}}{\unicode[STIX]{x1D71B}^{1/4}\unicode[STIX]{x1D6FF}_{1}^{2q}}}-\unicode[STIX]{x1D701}_{3}.\end{eqnarray}$$
Then, we have
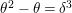 $\unicode[STIX]{x1D703}^{2}-\unicode[STIX]{x1D703}=\unicode[STIX]{x1D6FF}^{3}$
. Note that
$\unicode[STIX]{x1D703}^{2}-\unicode[STIX]{x1D703}=\unicode[STIX]{x1D6FF}^{3}$
. Note that
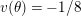 $v(\unicode[STIX]{x1D703})=-1/8$
. Let
$v(\unicode[STIX]{x1D703})=-1/8$
. Let
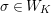 $\unicode[STIX]{x1D70E}\in W_{K}$
in this paragraph. We put
$\unicode[STIX]{x1D70E}\in W_{K}$
in this paragraph. We put
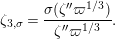 $$\begin{eqnarray}\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}={\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3})}{\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3}}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}={\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3})}{\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3}}}.\end{eqnarray}$$
We take
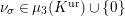 $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D707}_{3}(K^{\text{ur}})\cup \{0\}$
such that
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D707}_{3}(K^{\text{ur}})\cup \{0\}$
such that
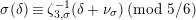 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})\equiv \unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}^{-1}(\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}})\;(\text{mod}~5/6)$
. Then, we have
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})\equiv \unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}^{-1}(\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}})\;(\text{mod}~5/6)$
. Then, we have
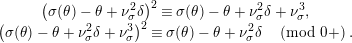 $$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle (\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D6FF})^{2}\equiv \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{3},\\ \displaystyle (\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{3})^{2}\equiv \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D6FF}\quad \left(\text{mod}~0+\right).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle (\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D6FF})^{2}\equiv \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{3},\\ \displaystyle (\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{3})^{2}\equiv \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D6FF}\quad \left(\text{mod}~0+\right).\end{array}\end{eqnarray}$$
By these equations, we can take
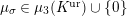 $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D707}_{3}(K^{\text{ur}})\cup \{0\}$
such that
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D707}_{3}(K^{\text{ur}})\cup \{0\}$
such that
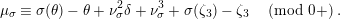 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}\equiv \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{3}+\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}_{3})-\unicode[STIX]{x1D701}_{3}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}\equiv \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{3}+\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}_{3})-\unicode[STIX]{x1D701}_{3}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
Then, we have
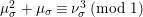 $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}^{2}+\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}\equiv \unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{3}\;(\text{mod}~1)$
by (6.8) and
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}^{2}+\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}\equiv \unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{3}\;(\text{mod}~1)$
by (6.8) and
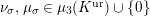 $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D707}_{3}(K^{\text{ur}})\cup \{0\}$
.
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D707}_{3}(K^{\text{ur}})\cup \{0\}$
.
Lemma 6.10.
-
(1) Let
 $\unicode[STIX]{x1D70E}\in W_{K}$
. Then, we have
$\unicode[STIX]{x1D70E}\in W_{K}$
. Then, we have  $$\begin{eqnarray}a_{\unicode[STIX]{x1D70E}}\equiv \unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}},\qquad b_{\unicode[STIX]{x1D70E}}\equiv \unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2},\qquad b_{\unicode[STIX]{x1D70E}}^{\prime }\equiv \unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}},\qquad c_{\unicode[STIX]{x1D70E}}\equiv \unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
$$\begin{eqnarray}a_{\unicode[STIX]{x1D70E}}\equiv \unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}},\qquad b_{\unicode[STIX]{x1D70E}}\equiv \unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2},\qquad b_{\unicode[STIX]{x1D70E}}^{\prime }\equiv \unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}},\qquad c_{\unicode[STIX]{x1D70E}}\equiv \unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
-
(2) Let
 $\unicode[STIX]{x1D70E}\in W_{K}$
. Then we have
$\unicode[STIX]{x1D70E}\in W_{K}$
. Then we have
 $\bar{a}_{\unicode[STIX]{x1D70E}}\in \mathbb{F}_{4}^{\times }$
and
$\bar{a}_{\unicode[STIX]{x1D70E}}\in \mathbb{F}_{4}^{\times }$
and
 $\bar{b}_{\unicode[STIX]{x1D70E}},\bar{b}_{\unicode[STIX]{x1D70E}}^{\prime },\bar{c}_{\unicode[STIX]{x1D70E}}\in \mathbb{F}_{4}$
. Further,
$\bar{b}_{\unicode[STIX]{x1D70E}},\bar{b}_{\unicode[STIX]{x1D70E}}^{\prime },\bar{c}_{\unicode[STIX]{x1D70E}}\in \mathbb{F}_{4}$
. Further,
 $\bar{a}_{\unicode[STIX]{x1D70E}}\bar{b}_{\unicode[STIX]{x1D70E}}^{2}=\bar{b}_{\unicode[STIX]{x1D70E}}^{\prime }$
and
$\bar{a}_{\unicode[STIX]{x1D70E}}\bar{b}_{\unicode[STIX]{x1D70E}}^{2}=\bar{b}_{\unicode[STIX]{x1D70E}}^{\prime }$
and
 $\bar{b}_{\unicode[STIX]{x1D70E}}^{3}=\bar{c}_{\unicode[STIX]{x1D70E}}^{2}+\bar{c}_{\unicode[STIX]{x1D70E}}$
hold.
$\bar{b}_{\unicode[STIX]{x1D70E}}^{3}=\bar{c}_{\unicode[STIX]{x1D70E}}^{2}+\bar{c}_{\unicode[STIX]{x1D70E}}$
hold.
Proof. By the definition of
![]() $b_{2,\unicode[STIX]{x1D701}^{\prime }}$
, we have
$b_{2,\unicode[STIX]{x1D701}^{\prime }}$
, we have
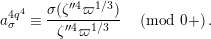 $$\begin{eqnarray}a_{\unicode[STIX]{x1D70E}}^{4q^{4}}\equiv {\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}^{\prime \prime 4}\unicode[STIX]{x1D71B}^{1/3})}{\unicode[STIX]{x1D701}^{\prime \prime 4}\unicode[STIX]{x1D71B}^{1/3}}}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
$$\begin{eqnarray}a_{\unicode[STIX]{x1D70E}}^{4q^{4}}\equiv {\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}^{\prime \prime 4}\unicode[STIX]{x1D71B}^{1/3})}{\unicode[STIX]{x1D701}^{\prime \prime 4}\unicode[STIX]{x1D71B}^{1/3}}}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
Hence, we have
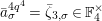 $\bar{a}_{\unicode[STIX]{x1D70E}}^{4q^{4}}=\bar{\unicode[STIX]{x1D701}}_{3,\unicode[STIX]{x1D70E}}\in \mathbb{F}_{4}^{\times }$
. This implies that
$\bar{a}_{\unicode[STIX]{x1D70E}}^{4q^{4}}=\bar{\unicode[STIX]{x1D701}}_{3,\unicode[STIX]{x1D70E}}\in \mathbb{F}_{4}^{\times }$
. This implies that
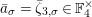 $\bar{a}_{\unicode[STIX]{x1D70E}}=\bar{\unicode[STIX]{x1D701}}_{3,\unicode[STIX]{x1D70E}}\in \mathbb{F}_{4}^{\times }$
.
$\bar{a}_{\unicode[STIX]{x1D70E}}=\bar{\unicode[STIX]{x1D701}}_{3,\unicode[STIX]{x1D70E}}\in \mathbb{F}_{4}^{\times }$
.
By the definition of
![]() $a_{1,\unicode[STIX]{x1D701}^{\prime }}$
and
$a_{1,\unicode[STIX]{x1D701}^{\prime }}$
and
![]() $b_{1,\unicode[STIX]{x1D701}^{\prime }}$
, we have
$b_{1,\unicode[STIX]{x1D701}^{\prime }}$
, we have
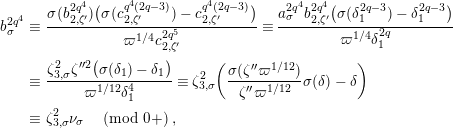 $$\begin{eqnarray}\displaystyle b_{\unicode[STIX]{x1D70E}}^{2q^{4}} & \equiv & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D70E}(b_{2,\unicode[STIX]{x1D701}^{\prime }}^{2q^{4}})(\unicode[STIX]{x1D70E}(c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}(2q-3)})-c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}(2q-3)})}{\unicode[STIX]{x1D71B}^{1/4}c_{2,\unicode[STIX]{x1D701}^{\prime }}^{2q^{5}}}}\equiv {\displaystyle \frac{a_{\unicode[STIX]{x1D70E}}^{2q^{4}}b_{2,\unicode[STIX]{x1D701}^{\prime }}^{2q^{4}}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}_{1}^{2q-3})-\unicode[STIX]{x1D6FF}_{1}^{2q-3})}{\unicode[STIX]{x1D71B}^{1/4}\unicode[STIX]{x1D6FF}_{1}^{2q}}}\nonumber\\ \displaystyle & \equiv & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D701}^{\prime \prime 2}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}_{1})-\unicode[STIX]{x1D6FF}_{1})}{\unicode[STIX]{x1D71B}^{1/12}\unicode[STIX]{x1D6FF}_{1}^{4}}}\equiv \unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}^{2}\biggl({\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12})}{\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12}}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})-\unicode[STIX]{x1D6FF}\biggr)\nonumber\\ \displaystyle & \equiv & \displaystyle \unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}\quad \left(\text{mod}~0+\right),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle b_{\unicode[STIX]{x1D70E}}^{2q^{4}} & \equiv & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D70E}(b_{2,\unicode[STIX]{x1D701}^{\prime }}^{2q^{4}})(\unicode[STIX]{x1D70E}(c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}(2q-3)})-c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}(2q-3)})}{\unicode[STIX]{x1D71B}^{1/4}c_{2,\unicode[STIX]{x1D701}^{\prime }}^{2q^{5}}}}\equiv {\displaystyle \frac{a_{\unicode[STIX]{x1D70E}}^{2q^{4}}b_{2,\unicode[STIX]{x1D701}^{\prime }}^{2q^{4}}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}_{1}^{2q-3})-\unicode[STIX]{x1D6FF}_{1}^{2q-3})}{\unicode[STIX]{x1D71B}^{1/4}\unicode[STIX]{x1D6FF}_{1}^{2q}}}\nonumber\\ \displaystyle & \equiv & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D701}^{\prime \prime 2}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}_{1})-\unicode[STIX]{x1D6FF}_{1})}{\unicode[STIX]{x1D71B}^{1/12}\unicode[STIX]{x1D6FF}_{1}^{4}}}\equiv \unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}^{2}\biggl({\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12})}{\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12}}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})-\unicode[STIX]{x1D6FF}\biggr)\nonumber\\ \displaystyle & \equiv & \displaystyle \unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}\quad \left(\text{mod}~0+\right),\nonumber\end{eqnarray}$$
where we use Lemma 6.8 in the second congruence,
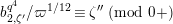 $b_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}}/\unicode[STIX]{x1D71B}^{1/12}\equiv \unicode[STIX]{x1D701}^{\prime \prime }\;(\text{mod}~0+)$
in the third congruence,
$b_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}}/\unicode[STIX]{x1D71B}^{1/12}\equiv \unicode[STIX]{x1D701}^{\prime \prime }\;(\text{mod}~0+)$
in the third congruence,
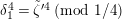 $\unicode[STIX]{x1D6FF}_{1}^{4}=\tilde{\unicode[STIX]{x1D701}}^{\prime 4}\;(\text{mod}~1/4)$
and
$\unicode[STIX]{x1D6FF}_{1}^{4}=\tilde{\unicode[STIX]{x1D701}}^{\prime 4}\;(\text{mod}~1/4)$
and
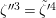 $\unicode[STIX]{x1D701}^{\prime \prime 3}=\tilde{\unicode[STIX]{x1D701}}^{\prime 4}$
in the fourth congruence, and
$\unicode[STIX]{x1D701}^{\prime \prime 3}=\tilde{\unicode[STIX]{x1D701}}^{\prime 4}$
in the fourth congruence, and
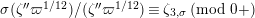 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12})/(\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12})\equiv \unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}\;(\text{mod}~0+)$
in the last congruence. Hence, we obtain
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12})/(\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12})\equiv \unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}\;(\text{mod}~0+)$
in the last congruence. Hence, we obtain
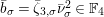 $\bar{b}_{\unicode[STIX]{x1D70E}}=\bar{\unicode[STIX]{x1D701}}_{3,\unicode[STIX]{x1D70E}}\bar{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D70E}}^{2}\in \mathbb{F}_{4}$
.
$\bar{b}_{\unicode[STIX]{x1D70E}}=\bar{\unicode[STIX]{x1D701}}_{3,\unicode[STIX]{x1D70E}}\bar{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D70E}}^{2}\in \mathbb{F}_{4}$
.
By Lemma 6.8 and
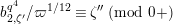 $b_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}}/\unicode[STIX]{x1D71B}^{1/12}\equiv \unicode[STIX]{x1D701}^{\prime \prime }\;(\text{mod}~0+)$
, we have
$b_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}}/\unicode[STIX]{x1D71B}^{1/12}\equiv \unicode[STIX]{x1D701}^{\prime \prime }\;(\text{mod}~0+)$
, we have
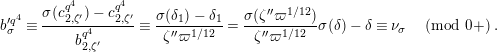 $$\begin{eqnarray}b_{\unicode[STIX]{x1D70E}}^{\prime q^{4}}\equiv {\displaystyle \frac{\unicode[STIX]{x1D70E}(c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}})-c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}}}{b_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}}}}\equiv {\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}_{1})-\unicode[STIX]{x1D6FF}_{1}}{\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12}}}={\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12})}{\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12}}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})-\unicode[STIX]{x1D6FF}\equiv \unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
$$\begin{eqnarray}b_{\unicode[STIX]{x1D70E}}^{\prime q^{4}}\equiv {\displaystyle \frac{\unicode[STIX]{x1D70E}(c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}})-c_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}}}{b_{2,\unicode[STIX]{x1D701}^{\prime }}^{q^{4}}}}\equiv {\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}_{1})-\unicode[STIX]{x1D6FF}_{1}}{\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12}}}={\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12})}{\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/12}}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})-\unicode[STIX]{x1D6FF}\equiv \unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
Hence, we obtain
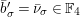 $\bar{b}_{\unicode[STIX]{x1D70E}}^{\prime }=\bar{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D70E}}\in \mathbb{F}_{4}$
.
$\bar{b}_{\unicode[STIX]{x1D70E}}^{\prime }=\bar{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D70E}}\in \mathbb{F}_{4}$
.
By Lemmas 6.8 and 6.9 and the definition of
![]() $a_{1,\unicode[STIX]{x1D701}^{\prime }}$
, we have
$a_{1,\unicode[STIX]{x1D701}^{\prime }}$
, we have
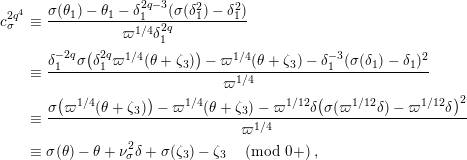 $$\begin{eqnarray}\displaystyle c_{\unicode[STIX]{x1D70E}}^{2q^{4}} & \equiv & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703}_{1})-\unicode[STIX]{x1D703}_{1}-\unicode[STIX]{x1D6FF}_{1}^{2q-3}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}_{1}^{2})-\unicode[STIX]{x1D6FF}_{1}^{2})}{\unicode[STIX]{x1D71B}^{1/4}\unicode[STIX]{x1D6FF}_{1}^{2q}}}\nonumber\\ \displaystyle & \equiv & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D6FF}_{1}^{-2q}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}_{1}^{2q}\unicode[STIX]{x1D71B}^{1/4}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D701}_{3}))-\unicode[STIX]{x1D71B}^{1/4}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D701}_{3})-\unicode[STIX]{x1D6FF}_{1}^{-3}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}_{1})-\unicode[STIX]{x1D6FF}_{1})^{2}}{\unicode[STIX]{x1D71B}^{1/4}}}\nonumber\\ \displaystyle & \equiv & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}^{1/4}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D701}_{3}))-\unicode[STIX]{x1D71B}^{1/4}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D701}_{3})-\unicode[STIX]{x1D71B}^{1/12}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}^{1/12}\unicode[STIX]{x1D6FF})-\unicode[STIX]{x1D71B}^{1/12}\unicode[STIX]{x1D6FF})^{2}}{\unicode[STIX]{x1D71B}^{1/4}}}\nonumber\\ \displaystyle & \equiv & \displaystyle \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}_{3})-\unicode[STIX]{x1D701}_{3}\quad \left(\text{mod}~0+\right),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{\unicode[STIX]{x1D70E}}^{2q^{4}} & \equiv & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703}_{1})-\unicode[STIX]{x1D703}_{1}-\unicode[STIX]{x1D6FF}_{1}^{2q-3}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}_{1}^{2})-\unicode[STIX]{x1D6FF}_{1}^{2})}{\unicode[STIX]{x1D71B}^{1/4}\unicode[STIX]{x1D6FF}_{1}^{2q}}}\nonumber\\ \displaystyle & \equiv & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D6FF}_{1}^{-2q}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}_{1}^{2q}\unicode[STIX]{x1D71B}^{1/4}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D701}_{3}))-\unicode[STIX]{x1D71B}^{1/4}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D701}_{3})-\unicode[STIX]{x1D6FF}_{1}^{-3}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}_{1})-\unicode[STIX]{x1D6FF}_{1})^{2}}{\unicode[STIX]{x1D71B}^{1/4}}}\nonumber\\ \displaystyle & \equiv & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}^{1/4}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D701}_{3}))-\unicode[STIX]{x1D71B}^{1/4}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D701}_{3})-\unicode[STIX]{x1D71B}^{1/12}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D71B}^{1/12}\unicode[STIX]{x1D6FF})-\unicode[STIX]{x1D71B}^{1/12}\unicode[STIX]{x1D6FF})^{2}}{\unicode[STIX]{x1D71B}^{1/4}}}\nonumber\\ \displaystyle & \equiv & \displaystyle \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}_{3})-\unicode[STIX]{x1D701}_{3}\quad \left(\text{mod}~0+\right),\nonumber\end{eqnarray}$$
where we use
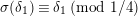 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}_{1})\equiv \unicode[STIX]{x1D6FF}_{1}\;(\text{mod}~1/4)$
in the second congruence, and
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF}_{1})\equiv \unicode[STIX]{x1D6FF}_{1}\;(\text{mod}~1/4)$
in the second congruence, and
 $\unicode[STIX]{x1D6FF}_{1}^{4}=\tilde{\unicode[STIX]{x1D701}}^{\prime 4}\;(\text{mod}~1/4)$
in the third congruence. Then, we have
$\unicode[STIX]{x1D6FF}_{1}^{4}=\tilde{\unicode[STIX]{x1D701}}^{\prime 4}\;(\text{mod}~1/4)$
in the third congruence. Then, we have
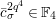 $\bar{c}_{\unicode[STIX]{x1D70E}}^{2q^{4}}\in \mathbb{F}_{4}$
by (6.8). Hence, we have
$\bar{c}_{\unicode[STIX]{x1D70E}}^{2q^{4}}\in \mathbb{F}_{4}$
by (6.8). Hence, we have
![]() $\bar{c}_{\unicode[STIX]{x1D70E}}\in \mathbb{F}_{4}$
and
$\bar{c}_{\unicode[STIX]{x1D70E}}\in \mathbb{F}_{4}$
and
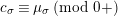 $c_{\unicode[STIX]{x1D70E}}\equiv \unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}\;(\text{mod}~0+)$
, again by (6.8).
$c_{\unicode[STIX]{x1D70E}}\equiv \unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}\;(\text{mod}~0+)$
, again by (6.8).
By the above calculations, we can easily check that
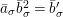 $\bar{a}_{\unicode[STIX]{x1D70E}}\bar{b}_{\unicode[STIX]{x1D70E}}^{2}=\bar{b}_{\unicode[STIX]{x1D70E}}^{\prime }$
and
$\bar{a}_{\unicode[STIX]{x1D70E}}\bar{b}_{\unicode[STIX]{x1D70E}}^{2}=\bar{b}_{\unicode[STIX]{x1D70E}}^{\prime }$
and
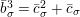 $\bar{b}_{\unicode[STIX]{x1D70E}}^{3}=\bar{c}_{\unicode[STIX]{x1D70E}}^{2}+\bar{c}_{\unicode[STIX]{x1D70E}}$
.◻
$\bar{b}_{\unicode[STIX]{x1D70E}}^{3}=\bar{c}_{\unicode[STIX]{x1D70E}}^{2}+\bar{c}_{\unicode[STIX]{x1D70E}}$
.◻
Lemma 6.11. The field
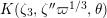 $K(\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})$
is a Galois extension over
$K(\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})$
is a Galois extension over
![]() $K$
.
$K$
.
Proof. Let
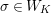 $\unicode[STIX]{x1D70E}\in W_{K}$
. It suffices to show that
$\unicode[STIX]{x1D70E}\in W_{K}$
. It suffices to show that
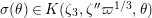 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\in K(\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})$
. We put
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\in K(\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})$
. We put
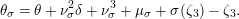 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{3}+\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}+\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}_{3})-\unicode[STIX]{x1D701}_{3}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{2}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}^{3}+\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}+\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D701}_{3})-\unicode[STIX]{x1D701}_{3}.\end{eqnarray}$$
Then, we have
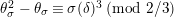 $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}}^{2}-\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}}\equiv \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})^{3}\;(\text{mod}~2/3)$
. Hence, we can find
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}}^{2}-\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}}\equiv \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})^{3}\;(\text{mod}~2/3)$
. Hence, we can find
![]() $\unicode[STIX]{x1D703}^{\prime }$
such that
$\unicode[STIX]{x1D703}^{\prime }$
such that
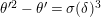 $\unicode[STIX]{x1D703}^{\prime 2}-\unicode[STIX]{x1D703}^{\prime }=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})^{3}$
and
$\unicode[STIX]{x1D703}^{\prime 2}-\unicode[STIX]{x1D703}^{\prime }=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})^{3}$
and
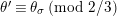 $\unicode[STIX]{x1D703}^{\prime }\equiv \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}}\;(\text{mod}~2/3)$
. By the choice of
$\unicode[STIX]{x1D703}^{\prime }\equiv \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}}\;(\text{mod}~2/3)$
. By the choice of
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}$
, we have
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}$
, we have
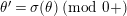 $\unicode[STIX]{x1D703}^{\prime }=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\;(\text{mod}~0+)$
. Hence, we obtain
$\unicode[STIX]{x1D703}^{\prime }=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\;(\text{mod}~0+)$
. Hence, we obtain
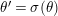 $\unicode[STIX]{x1D703}^{\prime }=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})$
.
$\unicode[STIX]{x1D703}^{\prime }=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})$
.
We take
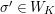 $\unicode[STIX]{x1D70E}^{\prime }\in W_{K}$
such that
$\unicode[STIX]{x1D70E}^{\prime }\in W_{K}$
such that
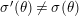 $\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D703})\neq \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})$
. We can define
$\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D703})\neq \unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})$
. We can define
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}^{\prime }}$
as above, and have
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}^{\prime }}$
as above, and have
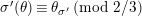 $\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D703})\equiv \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}^{\prime }}\;(\text{mod}~2/3)$
. If
$\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D703})\equiv \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}^{\prime }}\;(\text{mod}~2/3)$
. If
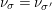 $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}^{\prime }}$
, then we have
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}^{\prime }}$
, then we have
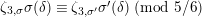 $\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})\equiv \unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}^{\prime }}\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D6FF})\;(\text{mod}~5/6)$
, which implies that
$\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})\equiv \unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}^{\prime }}\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D6FF})\;(\text{mod}~5/6)$
, which implies that
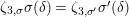 $\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}^{\prime }}\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D6FF})$
because both sides are roots of
$\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}^{\prime }}\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D6FF})$
because both sides are roots of
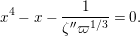 $$\begin{eqnarray}x^{4}-x-{\displaystyle \frac{1}{\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3}}}=0.\end{eqnarray}$$
$$\begin{eqnarray}x^{4}-x-{\displaystyle \frac{1}{\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3}}}=0.\end{eqnarray}$$
Hence, if
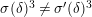 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})^{3}\neq \unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D6FF})^{3}$
, we have
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})^{3}\neq \unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D6FF})^{3}$
, we have
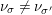 $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}\neq \unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}^{\prime }}$
, which implies that
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}\neq \unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}^{\prime }}$
, which implies that
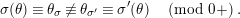 $$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\equiv \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}}\not \equiv \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}^{\prime }}\equiv \unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D703})\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\equiv \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}}\not \equiv \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}^{\prime }}\equiv \unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D703})\quad \left(\text{mod}~0+\right).\end{eqnarray}$$
If
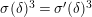 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})^{3}=\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D6FF})^{3}$
, we have
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FF})^{3}=\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D6FF})^{3}$
, we have
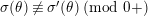 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\not \equiv \unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D703})\;(\text{mod}~0+)$
. Therefore, we have
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\not \equiv \unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D703})\;(\text{mod}~0+)$
. Therefore, we have
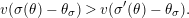 $$\begin{eqnarray}v(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}})>v(\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}}).\end{eqnarray}$$
$$\begin{eqnarray}v(\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}})>v(\unicode[STIX]{x1D70E}^{\prime }(\unicode[STIX]{x1D703})-\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}}).\end{eqnarray}$$
Then, we obtain
 $$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\in K(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}})\subset K(\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\in K(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}})\subset K(\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})\end{eqnarray}$$
by Krasner’s lemma. ◻
Let
![]() $E$
be the elliptic curve over
$E$
be the elliptic curve over
![]() $k^{\text{ac}}$
defined by
$k^{\text{ac}}$
defined by
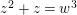 $z^{2}+z=w^{3}$
. We put
$z^{2}+z=w^{3}$
. We put
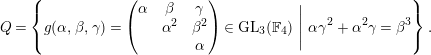 $$\begin{eqnarray}Q=\left\{g(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FD} & \unicode[STIX]{x1D6FE}\\ & \unicode[STIX]{x1D6FC}^{2} & \unicode[STIX]{x1D6FD}^{2}\\ & & \unicode[STIX]{x1D6FC}\end{array}\right)\in \text{GL}_{3}(\mathbb{F}_{4})~\Bigg|~\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}^{2}+\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FD}^{3}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}Q=\left\{g(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})=\left(\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FD} & \unicode[STIX]{x1D6FE}\\ & \unicode[STIX]{x1D6FC}^{2} & \unicode[STIX]{x1D6FD}^{2}\\ & & \unicode[STIX]{x1D6FC}\end{array}\right)\in \text{GL}_{3}(\mathbb{F}_{4})~\Bigg|~\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FE}^{2}+\unicode[STIX]{x1D6FC}^{2}\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FD}^{3}\right\}.\end{eqnarray}$$
We note that
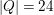 $|Q|=24$
and
$|Q|=24$
and
![]() $Q$
is isomorphic to
$Q$
is isomorphic to
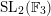 $\text{SL}_{2}(\mathbb{F}_{3})$
(cf. [Reference SerreSe, 8.5. Exercices 2]). Let
$\text{SL}_{2}(\mathbb{F}_{3})$
(cf. [Reference SerreSe, 8.5. Exercices 2]). Let
![]() $Q\rtimes \mathbb{Z}$
be a semidirect product, where
$Q\rtimes \mathbb{Z}$
be a semidirect product, where
![]() $r\in \mathbb{Z}$
acts on
$r\in \mathbb{Z}$
acts on
![]() $Q$
by
$Q$
by
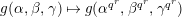 $g(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})\mapsto g(\unicode[STIX]{x1D6FC}^{q^{r}},\unicode[STIX]{x1D6FD}^{q^{r}},\unicode[STIX]{x1D6FE}^{q^{r}})$
. Then,
$g(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})\mapsto g(\unicode[STIX]{x1D6FC}^{q^{r}},\unicode[STIX]{x1D6FD}^{q^{r}},\unicode[STIX]{x1D6FE}^{q^{r}})$
. Then,
![]() $Q\rtimes \mathbb{Z}$
acts faithfully on
$Q\rtimes \mathbb{Z}$
acts faithfully on
![]() $E$
as a scheme over
$E$
as a scheme over
![]() $k$
, where
$k$
, where
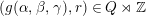 $(g(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}),r)\in Q\rtimes \mathbb{Z}$
acts on
$(g(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}),r)\in Q\rtimes \mathbb{Z}$
acts on
![]() $E$
by
$E$
by
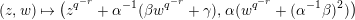 $$\begin{eqnarray}(z,w)\mapsto (z^{q^{-r}}+\unicode[STIX]{x1D6FC}^{-1}(\unicode[STIX]{x1D6FD}w^{q^{-r}}+\unicode[STIX]{x1D6FE}),\unicode[STIX]{x1D6FC}(w^{q^{-r}}+(\unicode[STIX]{x1D6FC}^{-1}\unicode[STIX]{x1D6FD})^{2}))\end{eqnarray}$$
$$\begin{eqnarray}(z,w)\mapsto (z^{q^{-r}}+\unicode[STIX]{x1D6FC}^{-1}(\unicode[STIX]{x1D6FD}w^{q^{-r}}+\unicode[STIX]{x1D6FE}),\unicode[STIX]{x1D6FC}(w^{q^{-r}}+(\unicode[STIX]{x1D6FC}^{-1}\unicode[STIX]{x1D6FD})^{2}))\end{eqnarray}$$
for
![]() $k^{\text{ac}}$
-valued points.
$k^{\text{ac}}$
-valued points.
Proposition 6.12. The element
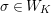 $\unicode[STIX]{x1D70E}\in W_{K}$
sends
$\unicode[STIX]{x1D70E}\in W_{K}$
sends
![]() $\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
to
$\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
to
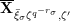 $\overline{\mathbf{X}}_{\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}},\unicode[STIX]{x1D701}^{\prime }}$
. We identify
$\overline{\mathbf{X}}_{\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}},\unicode[STIX]{x1D701}^{\prime }}$
. We identify
![]() $\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
with
$\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
with
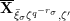 $\overline{\mathbf{X}}_{\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}},\unicode[STIX]{x1D701}^{\prime }}$
by
$\overline{\mathbf{X}}_{\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}^{q^{-r_{\unicode[STIX]{x1D70E}}}},\unicode[STIX]{x1D701}^{\prime }}$
by
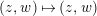 $(z,w)\mapsto (z,w)$
. Then, the action of
$(z,w)\mapsto (z,w)$
. Then, the action of
![]() $W_{K}$
gives a homomorphism
$W_{K}$
gives a homomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D701}^{\prime }}:W_{K}\rightarrow Q\rtimes \mathbb{Z}\subset \text{Aut}_{k}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }});\qquad \unicode[STIX]{x1D70E}\mapsto (g(\bar{\unicode[STIX]{x1D701}}_{3,\unicode[STIX]{x1D70E}},\bar{\unicode[STIX]{x1D701}}_{3,\unicode[STIX]{x1D70E}}^{2}\bar{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D70E}}^{2},\bar{\unicode[STIX]{x1D701}}_{3,\unicode[STIX]{x1D70E}}\bar{\unicode[STIX]{x1D707}}_{\unicode[STIX]{x1D70E}}),r_{\unicode[STIX]{x1D70E}}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D701}^{\prime }}:W_{K}\rightarrow Q\rtimes \mathbb{Z}\subset \text{Aut}_{k}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }});\qquad \unicode[STIX]{x1D70E}\mapsto (g(\bar{\unicode[STIX]{x1D701}}_{3,\unicode[STIX]{x1D70E}},\bar{\unicode[STIX]{x1D701}}_{3,\unicode[STIX]{x1D70E}}^{2}\bar{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D70E}}^{2},\bar{\unicode[STIX]{x1D701}}_{3,\unicode[STIX]{x1D70E}}\bar{\unicode[STIX]{x1D707}}_{\unicode[STIX]{x1D70E}}),r_{\unicode[STIX]{x1D70E}}).\end{eqnarray}$$
Proposition 6.13. The homomorphism
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D701}^{\prime }}$
factors through
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D701}^{\prime }}$
factors through
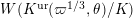 $W(K^{\text{ur}}(\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})/K)$
and gives an isomorphism
$W(K^{\text{ur}}(\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})/K)$
and gives an isomorphism
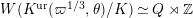 $W(K^{\text{ur}}(\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})/K)\simeq Q\rtimes \mathbb{Z}$
.
$W(K^{\text{ur}}(\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})/K)\simeq Q\rtimes \mathbb{Z}$
.
Proof. By Lemma 6.10(1), the homomorphism
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D701}^{\prime }}$
factors through
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D701}^{\prime }}$
factors through
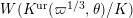 $W(K^{\text{ur}}(\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})/K)$
and induces an injective homomorphism
$W(K^{\text{ur}}(\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})/K)$
and induces an injective homomorphism
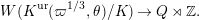 $$\begin{eqnarray}W(K^{\text{ur}}(\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})/K)\rightarrow Q\rtimes \mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}W(K^{\text{ur}}(\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})/K)\rightarrow Q\rtimes \mathbb{Z}.\end{eqnarray}$$
To prove the surjectivity, it suffices to show that
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D701}^{\prime }}$
sends
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D701}^{\prime }}$
sends
![]() $I_{K}$
onto
$I_{K}$
onto
![]() $Q$
. Let
$Q$
. Let
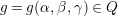 $g=g(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})\in Q$
. We take
$g=g(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})\in Q$
. We take
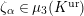 $\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D707}_{3}(K^{\text{ur}})$
,
$\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D707}_{3}(K^{\text{ur}})$
,
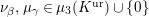 $\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}\in \unicode[STIX]{x1D707}_{3}(K^{\text{ur}})\cup \{0\}$
such that
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}\in \unicode[STIX]{x1D707}_{3}(K^{\text{ur}})\cup \{0\}$
such that
![]() $\bar{\unicode[STIX]{x1D701}}_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6FC}$
,
$\bar{\unicode[STIX]{x1D701}}_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D6FC}$
,
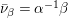 $\bar{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FC}^{-1}\unicode[STIX]{x1D6FD}$
and
$\bar{\unicode[STIX]{x1D708}}_{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FC}^{-1}\unicode[STIX]{x1D6FD}$
and
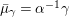 $\bar{\unicode[STIX]{x1D707}}_{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D6FC}^{-1}\unicode[STIX]{x1D6FE}$
. We put
$\bar{\unicode[STIX]{x1D707}}_{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D6FC}^{-1}\unicode[STIX]{x1D6FE}$
. We put
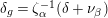 $\unicode[STIX]{x1D6FF}_{g}=\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FC}}^{-1}(\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}})$
and
$\unicode[STIX]{x1D6FF}_{g}=\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FC}}^{-1}(\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}})$
and
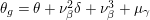 $\unicode[STIX]{x1D703}_{g}=\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}}^{2}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}}^{3}+\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}$
. Then, we have
$\unicode[STIX]{x1D703}_{g}=\unicode[STIX]{x1D703}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}}^{2}\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FD}}^{3}+\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FE}}$
. Then, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{g}^{4}-\unicode[STIX]{x1D6FF}_{g}\equiv {\displaystyle \frac{1}{\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3}}}\quad \left(\text{mod}~{\displaystyle \frac{5}{6}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{g}^{4}-\unicode[STIX]{x1D6FF}_{g}\equiv {\displaystyle \frac{1}{\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3}}}\quad \left(\text{mod}~{\displaystyle \frac{5}{6}}\right).\end{eqnarray}$$
Hence, we can find
![]() $\unicode[STIX]{x1D6FF}_{g}^{\prime }$
such that
$\unicode[STIX]{x1D6FF}_{g}^{\prime }$
such that
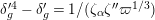 $\unicode[STIX]{x1D6FF}_{g}^{\prime 4}-\unicode[STIX]{x1D6FF}_{g}^{\prime }=1/(\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3})$
and
$\unicode[STIX]{x1D6FF}_{g}^{\prime 4}-\unicode[STIX]{x1D6FF}_{g}^{\prime }=1/(\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D701}^{\prime \prime }\unicode[STIX]{x1D71B}^{1/3})$
and
![]() $\unicode[STIX]{x1D6FF}_{g}^{\prime }\equiv \unicode[STIX]{x1D6FF}_{g}$
$\unicode[STIX]{x1D6FF}_{g}^{\prime }\equiv \unicode[STIX]{x1D6FF}_{g}$
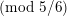 $(\text{mod}~5/6)$
. Further, we have
$(\text{mod}~5/6)$
. Further, we have
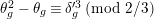 $\unicode[STIX]{x1D703}_{g}^{2}-\unicode[STIX]{x1D703}_{g}\equiv \unicode[STIX]{x1D6FF}_{g}^{\prime 3}\;(\text{mod}~2/3)$
. Hence, we can find
$\unicode[STIX]{x1D703}_{g}^{2}-\unicode[STIX]{x1D703}_{g}\equiv \unicode[STIX]{x1D6FF}_{g}^{\prime 3}\;(\text{mod}~2/3)$
. Hence, we can find
![]() $\unicode[STIX]{x1D703}_{g}^{\prime }$
such that
$\unicode[STIX]{x1D703}_{g}^{\prime }$
such that
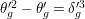 $\unicode[STIX]{x1D703}_{g}^{\prime 2}-\unicode[STIX]{x1D703}_{g}^{\prime }=\unicode[STIX]{x1D6FF}_{g}^{\prime 3}$
and
$\unicode[STIX]{x1D703}_{g}^{\prime 2}-\unicode[STIX]{x1D703}_{g}^{\prime }=\unicode[STIX]{x1D6FF}_{g}^{\prime 3}$
and
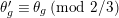 $\unicode[STIX]{x1D703}_{g}^{\prime }\equiv \unicode[STIX]{x1D703}_{g}\;(\text{mod}~2/3)$
. Then,
$\unicode[STIX]{x1D703}_{g}^{\prime }\equiv \unicode[STIX]{x1D703}_{g}\;(\text{mod}~2/3)$
. Then,
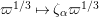 $\unicode[STIX]{x1D71B}^{1/3}\mapsto \unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D71B}^{1/3}$
, and
$\unicode[STIX]{x1D71B}^{1/3}\mapsto \unicode[STIX]{x1D701}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D71B}^{1/3}$
, and
![]() $\unicode[STIX]{x1D703}\mapsto \unicode[STIX]{x1D703}_{g}^{\prime }$
gives an element of
$\unicode[STIX]{x1D703}\mapsto \unicode[STIX]{x1D703}_{g}^{\prime }$
gives an element of
![]() $I_{K}$
, whose image by
$I_{K}$
, whose image by
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D701}^{\prime }}$
is
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D701}^{\prime }}$
is
![]() $g$
.◻
$g$
.◻
7 Cohomology of
 $\mathbf{X}_{1}(\mathfrak{p}^{3})$
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
In this section, we show that the covering
![]() ${\mathcal{C}}_{1}(\mathfrak{p}^{3})$
is semistable, and study a structure of
${\mathcal{C}}_{1}(\mathfrak{p}^{3})$
is semistable, and study a structure of
![]() $\ell$
-adic cohomology of
$\ell$
-adic cohomology of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
. In the following, for a projective smooth curve
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
. In the following, for a projective smooth curve
![]() $X$
over
$X$
over
![]() $k$
, we simply write
$k$
, we simply write
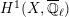 $H^{1}(X,\overline{\mathbb{Q}}_{\ell })$
for
$H^{1}(X,\overline{\mathbb{Q}}_{\ell })$
for
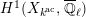 $H^{1}(X_{k^{\text{ac}}},\overline{\mathbb{Q}}_{\ell })$
. For a finite abelian group
$H^{1}(X_{k^{\text{ac}}},\overline{\mathbb{Q}}_{\ell })$
. For a finite abelian group
![]() $A$
, the character group
$A$
, the character group
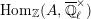 $\text{Hom}_{\mathbb{Z}}(A,\overline{\mathbb{Q}}_{\ell }^{\times })$
is denoted by
$\text{Hom}_{\mathbb{Z}}(A,\overline{\mathbb{Q}}_{\ell }^{\times })$
is denoted by
![]() $A^{\vee }$
.
$A^{\vee }$
.
7.1 Cohomology of reductions
Let
![]() $X_{\text{DL}}$
be the smooth compactification of the affine curve over
$X_{\text{DL}}$
be the smooth compactification of the affine curve over
![]() $k$
defined by
$k$
defined by
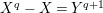 $X^{q}-X=Y^{q+1}$
. The curve
$X^{q}-X=Y^{q+1}$
. The curve
![]() $X_{\text{DL}}$
is also the smooth compactification of the Deligne–Lusztig curve
$X_{\text{DL}}$
is also the smooth compactification of the Deligne–Lusztig curve
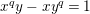 $x^{q}y-xy^{q}=1$
for
$x^{q}y-xy^{q}=1$
for
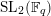 $\text{SL}_{2}(\mathbb{F}_{q})$
. Then,
$\text{SL}_{2}(\mathbb{F}_{q})$
. Then,
![]() $a\in k$
acts on
$a\in k$
acts on
![]() $X_{\text{DL}}$
by
$X_{\text{DL}}$
by
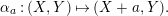 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{a}:(X,Y)\mapsto (X+a,Y).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{a}:(X,Y)\mapsto (X+a,Y).\end{eqnarray}$$
On the other hand,
![]() $\unicode[STIX]{x1D701}\in k_{2}^{\times }$
acts on
$\unicode[STIX]{x1D701}\in k_{2}^{\times }$
acts on
![]() $X_{\text{DL}}$
by
$X_{\text{DL}}$
by
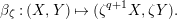 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}}:(X,Y)\mapsto (\unicode[STIX]{x1D701}^{q+1}X,\unicode[STIX]{x1D701}Y).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}}:(X,Y)\mapsto (\unicode[STIX]{x1D701}^{q+1}X,\unicode[STIX]{x1D701}Y).\end{eqnarray}$$
By these actions, we consider
 $H^{1}(X_{\text{DL}},\overline{\mathbb{Q}}_{\ell })$
as a
$H^{1}(X_{\text{DL}},\overline{\mathbb{Q}}_{\ell })$
as a
 $\overline{\mathbb{Q}}_{\ell }[k\times k_{2}^{\times }]$
-module.
$\overline{\mathbb{Q}}_{\ell }[k\times k_{2}^{\times }]$
-module.
Lemma 7.1. We have an isomorphism
 $$\begin{eqnarray}H^{1}(X_{\text{DL}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}}\bigoplus _{\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{q+1}(k_{2})^{\vee }\backslash \{1\}}\unicode[STIX]{x1D713}\otimes \unicode[STIX]{x1D712}\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(X_{\text{DL}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}}\bigoplus _{\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{q+1}(k_{2})^{\vee }\backslash \{1\}}\unicode[STIX]{x1D713}\otimes \unicode[STIX]{x1D712}\end{eqnarray}$$
as
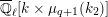 $\overline{\mathbb{Q}}_{\ell }[k\times \unicode[STIX]{x1D707}_{q+1}(k_{2})]$
-modules.
$\overline{\mathbb{Q}}_{\ell }[k\times \unicode[STIX]{x1D707}_{q+1}(k_{2})]$
-modules.
Proof. As
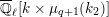 $\overline{\mathbb{Q}}_{\ell }[k\times \unicode[STIX]{x1D707}_{q+1}(k_{2})]$
-modules, we have the short exact sequence
$\overline{\mathbb{Q}}_{\ell }[k\times \unicode[STIX]{x1D707}_{q+1}(k_{2})]$
-modules, we have the short exact sequence
 $$\begin{eqnarray}0\rightarrow \bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }}\unicode[STIX]{x1D713}\rightarrow H_{c}^{1}(X_{\text{DL}}\backslash X_{\text{DL}}(k),\overline{\mathbb{Q}}_{\ell })\rightarrow H^{1}(X_{\text{DL}},\overline{\mathbb{Q}}_{\ell })\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }}\unicode[STIX]{x1D713}\rightarrow H_{c}^{1}(X_{\text{DL}}\backslash X_{\text{DL}}(k),\overline{\mathbb{Q}}_{\ell })\rightarrow H^{1}(X_{\text{DL}},\overline{\mathbb{Q}}_{\ell })\rightarrow 0.\end{eqnarray}$$
Let
![]() ${\mathcal{L}}_{\unicode[STIX]{x1D713}}$
denote the Artin–Schreier
${\mathcal{L}}_{\unicode[STIX]{x1D713}}$
denote the Artin–Schreier
![]() $\overline{\mathbb{Q}}_{\ell }$
-sheaf associated to
$\overline{\mathbb{Q}}_{\ell }$
-sheaf associated to
![]() $\unicode[STIX]{x1D713}\in k^{\vee }$
. Let
$\unicode[STIX]{x1D713}\in k^{\vee }$
. Let
![]() ${\mathcal{K}}_{\unicode[STIX]{x1D712}}$
denote the Kummer
${\mathcal{K}}_{\unicode[STIX]{x1D712}}$
denote the Kummer
![]() $\overline{\mathbb{Q}}_{\ell }$
-sheaf associated to
$\overline{\mathbb{Q}}_{\ell }$
-sheaf associated to
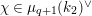 $\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{q+1}(k_{2})^{\vee }$
. Since
$\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{q+1}(k_{2})^{\vee }$
. Since
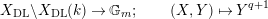 $$\begin{eqnarray}X_{\text{DL}}\backslash X_{\text{DL}}(k)\rightarrow \mathbb{G}_{m};\qquad (X,Y)\mapsto Y^{q+1}\end{eqnarray}$$
$$\begin{eqnarray}X_{\text{DL}}\backslash X_{\text{DL}}(k)\rightarrow \mathbb{G}_{m};\qquad (X,Y)\mapsto Y^{q+1}\end{eqnarray}$$
is a finite etale Galois covering with a Galois group
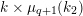 $k\times \unicode[STIX]{x1D707}_{q+1}(k_{2})$
, we have the isomorphism
$k\times \unicode[STIX]{x1D707}_{q+1}(k_{2})$
, we have the isomorphism
 $$\begin{eqnarray}H_{c}^{1}(X_{\text{DL}}\backslash X_{\text{DL}}(k),\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }}\bigoplus _{\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{q+1}(k_{2})^{\vee }}H_{c}^{1}(\mathbb{G}_{m},{\mathcal{L}}_{\unicode[STIX]{x1D713}}\otimes {\mathcal{K}}_{\unicode[STIX]{x1D712}})\end{eqnarray}$$
$$\begin{eqnarray}H_{c}^{1}(X_{\text{DL}}\backslash X_{\text{DL}}(k),\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }}\bigoplus _{\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{q+1}(k_{2})^{\vee }}H_{c}^{1}(\mathbb{G}_{m},{\mathcal{L}}_{\unicode[STIX]{x1D713}}\otimes {\mathcal{K}}_{\unicode[STIX]{x1D712}})\end{eqnarray}$$
as
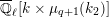 $\overline{\mathbb{Q}}_{\ell }[k\times \unicode[STIX]{x1D707}_{q+1}(k_{2})]$
-modules. Note that we have
$\overline{\mathbb{Q}}_{\ell }[k\times \unicode[STIX]{x1D707}_{q+1}(k_{2})]$
-modules. Note that we have
 $$\begin{eqnarray}\dim H_{c}^{1}(\mathbb{G}_{m},{\mathcal{L}}_{\unicode[STIX]{x1D713}}\otimes {\mathcal{K}}_{\unicode[STIX]{x1D712}})=1\end{eqnarray}$$
$$\begin{eqnarray}\dim H_{c}^{1}(\mathbb{G}_{m},{\mathcal{L}}_{\unicode[STIX]{x1D713}}\otimes {\mathcal{K}}_{\unicode[STIX]{x1D712}})=1\end{eqnarray}$$
if
![]() $\unicode[STIX]{x1D713}\neq 1$
by the Grothendieck–Ogg–Shafarevich formula (cf. [Reference GrothendieckSGA5, Exposé X, Théorème 7.1]). Clearly, if
$\unicode[STIX]{x1D713}\neq 1$
by the Grothendieck–Ogg–Shafarevich formula (cf. [Reference GrothendieckSGA5, Exposé X, Théorème 7.1]). Clearly, if
![]() $\unicode[STIX]{x1D712}\neq 1$
, we have
$\unicode[STIX]{x1D712}\neq 1$
, we have
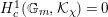 $H_{c}^{1}(\mathbb{G}_{m},{\mathcal{K}}_{\unicode[STIX]{x1D712}})=0$
and
$H_{c}^{1}(\mathbb{G}_{m},{\mathcal{K}}_{\unicode[STIX]{x1D712}})=0$
and
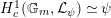 $H_{c}^{1}(\mathbb{G}_{m},{\mathcal{L}}_{\unicode[STIX]{x1D713}})\simeq \unicode[STIX]{x1D713}$
. Hence, we acquire the isomorphism
$H_{c}^{1}(\mathbb{G}_{m},{\mathcal{L}}_{\unicode[STIX]{x1D713}})\simeq \unicode[STIX]{x1D713}$
. Hence, we acquire the isomorphism
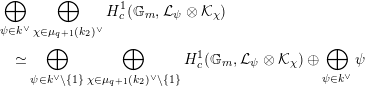 $$\begin{eqnarray}\displaystyle & & \displaystyle \bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }}\bigoplus _{\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{q+1}(k_{2})^{\vee }}H_{c}^{1}(\mathbb{G}_{m},{\mathcal{L}}_{\unicode[STIX]{x1D713}}\otimes {\mathcal{K}}_{\unicode[STIX]{x1D712}})\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }\setminus \{1\}}\bigoplus _{\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{q+1}(k_{2})^{\vee }\setminus \{1\}}H_{c}^{1}(\mathbb{G}_{m},{\mathcal{L}}_{\unicode[STIX]{x1D713}}\otimes {\mathcal{K}}_{\unicode[STIX]{x1D712}})\oplus \bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }}\unicode[STIX]{x1D713}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }}\bigoplus _{\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{q+1}(k_{2})^{\vee }}H_{c}^{1}(\mathbb{G}_{m},{\mathcal{L}}_{\unicode[STIX]{x1D713}}\otimes {\mathcal{K}}_{\unicode[STIX]{x1D712}})\nonumber\\ \displaystyle & & \displaystyle \quad \simeq \bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }\setminus \{1\}}\bigoplus _{\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{q+1}(k_{2})^{\vee }\setminus \{1\}}H_{c}^{1}(\mathbb{G}_{m},{\mathcal{L}}_{\unicode[STIX]{x1D713}}\otimes {\mathcal{K}}_{\unicode[STIX]{x1D712}})\oplus \bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }}\unicode[STIX]{x1D713}\end{eqnarray}$$
as
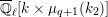 $\overline{\mathbb{Q}}_{\ell }[k\times \unicode[STIX]{x1D707}_{q+1}(k_{2})]$
-modules. By (7.1), (7.2) and (7.3), the required assertion follows.◻
$\overline{\mathbb{Q}}_{\ell }[k\times \unicode[STIX]{x1D707}_{q+1}(k_{2})]$
-modules. By (7.1), (7.2) and (7.3), the required assertion follows.◻
For a character
![]() $\unicode[STIX]{x1D713}\in k^{\vee }$
and an element
$\unicode[STIX]{x1D713}\in k^{\vee }$
and an element
![]() $\unicode[STIX]{x1D701}\in k^{\times }$
, we denote by
$\unicode[STIX]{x1D701}\in k^{\times }$
, we denote by
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D701}}$
the character
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D701}}$
the character
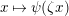 $x\mapsto \unicode[STIX]{x1D713}(\unicode[STIX]{x1D701}x)$
. We consider a character group
$x\mapsto \unicode[STIX]{x1D713}(\unicode[STIX]{x1D701}x)$
. We consider a character group
![]() $(k^{\times })^{\vee }$
as a subgroup of
$(k^{\times })^{\vee }$
as a subgroup of
![]() $(k_{2}^{\times })^{\vee }$
by
$(k_{2}^{\times })^{\vee }$
by
![]() $\text{Nr}_{k_{2}/k}^{\vee }$
.
$\text{Nr}_{k_{2}/k}^{\vee }$
.
Lemma 7.2. We have an isomorphism
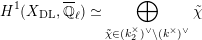 $$\begin{eqnarray}H^{1}(X_{\text{DL}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\tilde{\unicode[STIX]{x1D712}}\in (k_{2}^{\times })^{\vee }\backslash (k^{\times })^{\vee }}\tilde{\unicode[STIX]{x1D712}}\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(X_{\text{DL}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\tilde{\unicode[STIX]{x1D712}}\in (k_{2}^{\times })^{\vee }\backslash (k^{\times })^{\vee }}\tilde{\unicode[STIX]{x1D712}}\end{eqnarray}$$
as
![]() $\overline{\mathbb{Q}}_{\ell }[k_{2}^{\times }]$
-modules.
$\overline{\mathbb{Q}}_{\ell }[k_{2}^{\times }]$
-modules.
Proof. By Lemma 7.1, we take a basis
 $$\begin{eqnarray}\{e_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712}}\}_{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\},\,\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{q+1}(k_{2})^{\vee }\backslash \{1\}}\end{eqnarray}$$
$$\begin{eqnarray}\{e_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712}}\}_{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\},\,\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{q+1}(k_{2})^{\vee }\backslash \{1\}}\end{eqnarray}$$
of
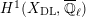 $H^{1}(X_{\text{DL}},\overline{\mathbb{Q}}_{\ell })$
over
$H^{1}(X_{\text{DL}},\overline{\mathbb{Q}}_{\ell })$
over
![]() $\overline{\mathbb{Q}}_{\ell }$
such that
$\overline{\mathbb{Q}}_{\ell }$
such that
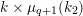 $k\times \unicode[STIX]{x1D707}_{q+1}(k_{2})$
acts on
$k\times \unicode[STIX]{x1D707}_{q+1}(k_{2})$
acts on
![]() $e_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712}}$
by
$e_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712}}$
by
![]() $\unicode[STIX]{x1D713}\otimes \unicode[STIX]{x1D712}$
. For
$\unicode[STIX]{x1D713}\otimes \unicode[STIX]{x1D712}$
. For
![]() $\unicode[STIX]{x1D701}\in k_{2}^{\times }$
and
$\unicode[STIX]{x1D701}\in k_{2}^{\times }$
and
![]() $a\in k$
, we have
$a\in k$
, we have
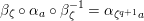 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}}\circ \unicode[STIX]{x1D6FC}_{a}\circ \unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}}^{-1}=\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D701}^{q+1}a}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}}\circ \unicode[STIX]{x1D6FC}_{a}\circ \unicode[STIX]{x1D6FD}_{\unicode[STIX]{x1D701}}^{-1}=\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D701}^{q+1}a}\end{eqnarray}$$
in
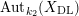 $\text{Aut}_{k_{2}}(X_{\text{DL}})$
. Hence,
$\text{Aut}_{k_{2}}(X_{\text{DL}})$
. Hence,
![]() $\unicode[STIX]{x1D701}\in k_{2}^{\times }$
acts on
$\unicode[STIX]{x1D701}\in k_{2}^{\times }$
acts on
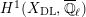 $H^{1}(X_{\text{DL}},\overline{\mathbb{Q}}_{\ell })$
by
$H^{1}(X_{\text{DL}},\overline{\mathbb{Q}}_{\ell })$
by
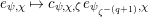 $$\begin{eqnarray}e_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712}}\mapsto c_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712},\unicode[STIX]{x1D701}}e_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D701}^{-(q+1)}},\unicode[STIX]{x1D712}}\end{eqnarray}$$
$$\begin{eqnarray}e_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712}}\mapsto c_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712},\unicode[STIX]{x1D701}}e_{\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D701}^{-(q+1)}},\unicode[STIX]{x1D712}}\end{eqnarray}$$
with some constant
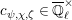 $c_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712},\unicode[STIX]{x1D701}}\in \overline{\mathbb{Q}}_{\ell }^{\times }$
. Therefore, we acquire an isomorphism
$c_{\unicode[STIX]{x1D713},\unicode[STIX]{x1D712},\unicode[STIX]{x1D701}}\in \overline{\mathbb{Q}}_{\ell }^{\times }$
. Therefore, we acquire an isomorphism
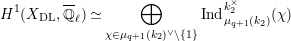 $$\begin{eqnarray}H^{1}(X_{\text{DL}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{q+1}(k_{2})^{\vee }\backslash \{1\}}\text{Ind}_{\unicode[STIX]{x1D707}_{q+1}(k_{2})}^{k_{2}^{\times }}(\unicode[STIX]{x1D712})\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(X_{\text{DL}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in \unicode[STIX]{x1D707}_{q+1}(k_{2})^{\vee }\backslash \{1\}}\text{Ind}_{\unicode[STIX]{x1D707}_{q+1}(k_{2})}^{k_{2}^{\times }}(\unicode[STIX]{x1D712})\end{eqnarray}$$
as
![]() $\overline{\mathbb{Q}}_{\ell }[k_{2}^{\times }]$
-modules. Hence, the required assertion follows.◻
$\overline{\mathbb{Q}}_{\ell }[k_{2}^{\times }]$
-modules. Hence, the required assertion follows.◻
Proposition 7.3. We have isomorphisms
 $$\begin{eqnarray}\displaystyle & \displaystyle H^{1}(\overline{\mathbf{Y}}_{1,2}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\tilde{\unicode[STIX]{x1D712}}\in (k_{2}^{\times })^{\vee }\backslash (k^{\times })^{\vee }}(\tilde{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D706})\otimes (\tilde{\unicode[STIX]{x1D712}}^{q}\circ \unicode[STIX]{x1D705}_{1}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle H^{1}(\overline{\mathbf{Y}}_{2,1}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\tilde{\unicode[STIX]{x1D712}}\in (k_{2}^{\times })^{\vee }\backslash (k^{\times })^{\vee }}(\tilde{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D706})\otimes (\tilde{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D705}_{1}) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle H^{1}(\overline{\mathbf{Y}}_{1,2}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\tilde{\unicode[STIX]{x1D712}}\in (k_{2}^{\times })^{\vee }\backslash (k^{\times })^{\vee }}(\tilde{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D706})\otimes (\tilde{\unicode[STIX]{x1D712}}^{q}\circ \unicode[STIX]{x1D705}_{1}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle H^{1}(\overline{\mathbf{Y}}_{2,1}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\tilde{\unicode[STIX]{x1D712}}\in (k_{2}^{\times })^{\vee }\backslash (k^{\times })^{\vee }}(\tilde{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D706})\otimes (\tilde{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D705}_{1}) & \displaystyle \nonumber\end{eqnarray}$$
as
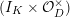 $(I_{K}\times {\mathcal{O}}_{D}^{\times })$
-representations over
$(I_{K}\times {\mathcal{O}}_{D}^{\times })$
-representations over
![]() $\overline{\mathbb{Q}}_{\ell }$
.
$\overline{\mathbb{Q}}_{\ell }$
.
Let
![]() $X_{\text{AS}}$
be the smooth compactification of the affine curve
$X_{\text{AS}}$
be the smooth compactification of the affine curve
![]() $X_{\text{AS}}^{\prime }$
over
$X_{\text{AS}}^{\prime }$
over
![]() $k$
defined by
$k$
defined by
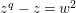 $z^{q}-z=w^{2}$
. Let
$z^{q}-z=w^{2}$
. Let
![]() $a\in k$
act on
$a\in k$
act on
![]() $X_{\text{AS}}$
by
$X_{\text{AS}}$
by
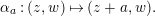 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{a}:(z,w)\mapsto (z+a,w).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{a}:(z,w)\mapsto (z+a,w).\end{eqnarray}$$
By this action, we consider
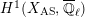 $H^{1}(X_{\text{AS}},\overline{\mathbb{Q}}_{\ell })$
as a
$H^{1}(X_{\text{AS}},\overline{\mathbb{Q}}_{\ell })$
as a
![]() $\overline{\mathbb{Q}}_{\ell }[k]$
-module. On the other hand, let
$\overline{\mathbb{Q}}_{\ell }[k]$
-module. On the other hand, let
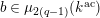 $b\in \unicode[STIX]{x1D707}_{2(q-1)}(k^{\text{ac}})$
act on
$b\in \unicode[STIX]{x1D707}_{2(q-1)}(k^{\text{ac}})$
act on
![]() $X_{\text{AS}}$
by
$X_{\text{AS}}$
by
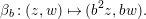 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{b}:(z,w)\mapsto (b^{2}z,bw).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{b}:(z,w)\mapsto (b^{2}z,bw).\end{eqnarray}$$
Lemma 7.4. We assume that
![]() $q$
is odd. Let
$q$
is odd. Let
![]() $G$
be the Galois group of the Galois extension
$G$
be the Galois group of the Galois extension
![]() $F$
over
$F$
over
![]() $k((s))$
defined by
$k((s))$
defined by
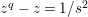 $z^{q}-z=1/s^{2}$
. Let
$z^{q}-z=1/s^{2}$
. Let
![]() $G^{r}$
be the upper numbering ramification filtration of
$G^{r}$
be the upper numbering ramification filtration of
![]() $G$
. Then,
$G$
. Then,
![]() $G^{r}=G$
if
$G^{r}=G$
if
![]() $r\leqslant 2$
, and
$r\leqslant 2$
, and
![]() $G^{r}=1$
if
$G^{r}=1$
if
![]() $r>2$
.
$r>2$
.
Proof. We take
![]() $a\in F$
such that
$a\in F$
such that
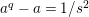 $a^{q}-a=1/s^{2}$
. Then,
$a^{q}-a=1/s^{2}$
. Then,
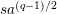 $sa^{(q-1)/2}$
is a uniformizer of
$sa^{(q-1)/2}$
is a uniformizer of
![]() $F$
. Let
$F$
. Let
![]() $v_{F}$
be the normalized valuation of
$v_{F}$
be the normalized valuation of
![]() $F$
. For
$F$
. For
![]() $\unicode[STIX]{x1D70E}\in G$
and an integer
$\unicode[STIX]{x1D70E}\in G$
and an integer
![]() $i$
, the condition
$i$
, the condition
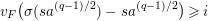 $$\begin{eqnarray}v_{F}(\unicode[STIX]{x1D70E}(sa^{(q-1)/2})-sa^{(q-1)/2})\geqslant i\end{eqnarray}$$
$$\begin{eqnarray}v_{F}(\unicode[STIX]{x1D70E}(sa^{(q-1)/2})-sa^{(q-1)/2})\geqslant i\end{eqnarray}$$
is equivalent to the condition
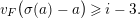 $$\begin{eqnarray}v_{F}(\unicode[STIX]{x1D70E}(a)-a)\geqslant i-3.\end{eqnarray}$$
$$\begin{eqnarray}v_{F}(\unicode[STIX]{x1D70E}(a)-a)\geqslant i-3.\end{eqnarray}$$
Hence, the claim follows. ◻
For a character
![]() $\unicode[STIX]{x1D713}\in k^{\vee }$
and
$\unicode[STIX]{x1D713}\in k^{\vee }$
and
![]() $x\in k^{\times }$
, we write
$x\in k^{\times }$
, we write
 $\unicode[STIX]{x1D713}_{x}\in k^{\vee }$
for the character
$\unicode[STIX]{x1D713}_{x}\in k^{\vee }$
for the character
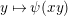 $y\mapsto \unicode[STIX]{x1D713}(xy)$
. We set
$y\mapsto \unicode[STIX]{x1D713}(xy)$
. We set
 $$\begin{eqnarray}V=\bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}}\unicode[STIX]{x1D713}\end{eqnarray}$$
$$\begin{eqnarray}V=\bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}}\unicode[STIX]{x1D713}\end{eqnarray}$$
as
![]() $\overline{\mathbb{Q}}_{\ell }[k]$
-modules. Let
$\overline{\mathbb{Q}}_{\ell }[k]$
-modules. Let
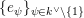 $\{e_{\unicode[STIX]{x1D713}}\}_{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}}$
be the standard basis of
$\{e_{\unicode[STIX]{x1D713}}\}_{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}}$
be the standard basis of
![]() $V$
.
$V$
.
Lemma 7.5. We assume that
![]() $q$
is odd.
$q$
is odd.
-
(1) Then, we have
 $H^{1}(X_{\text{AS}},\overline{\mathbb{Q}}_{\ell })\simeq V$
as
$H^{1}(X_{\text{AS}},\overline{\mathbb{Q}}_{\ell })\simeq V$
as
 $\overline{\mathbb{Q}}_{\ell }[k]$
-modules.
$\overline{\mathbb{Q}}_{\ell }[k]$
-modules. -
(2) For
 $b\in \unicode[STIX]{x1D707}_{2(q-1)}(k^{\text{ac}})$
, the automorphism
$b\in \unicode[STIX]{x1D707}_{2(q-1)}(k^{\text{ac}})$
, the automorphism
 $\unicode[STIX]{x1D6FD}_{b}$
of
$\unicode[STIX]{x1D6FD}_{b}$
of
 $X_{\text{AS}}$
induces the action on
$X_{\text{AS}}$
induces the action on $$\begin{eqnarray}e_{\unicode[STIX]{x1D713}}\mapsto c_{\unicode[STIX]{x1D713},b}e_{\unicode[STIX]{x1D713}_{b^{-2}}}\end{eqnarray}$$
$$\begin{eqnarray}e_{\unicode[STIX]{x1D713}}\mapsto c_{\unicode[STIX]{x1D713},b}e_{\unicode[STIX]{x1D713}_{b^{-2}}}\end{eqnarray}$$
 $H^{1}(X_{\text{AS}},\overline{\mathbb{Q}}_{\ell })\simeq V$
with some constant
$H^{1}(X_{\text{AS}},\overline{\mathbb{Q}}_{\ell })\simeq V$
with some constant
 $c_{\unicode[STIX]{x1D713},b}\in \overline{\mathbb{Q}}_{\ell }^{\times }$
. Furthermore, we have
$c_{\unicode[STIX]{x1D713},b}\in \overline{\mathbb{Q}}_{\ell }^{\times }$
. Furthermore, we have
 $c_{\unicode[STIX]{x1D713},-1}=-1$
.
$c_{\unicode[STIX]{x1D713},-1}=-1$
.
Proof. We have
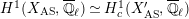 $H^{1}(X_{\text{AS}},\overline{\mathbb{Q}}_{\ell })\simeq H_{c}^{1}(X_{\text{AS}}^{\prime },\overline{\mathbb{Q}}_{\ell })$
, because the complement
$H^{1}(X_{\text{AS}},\overline{\mathbb{Q}}_{\ell })\simeq H_{c}^{1}(X_{\text{AS}}^{\prime },\overline{\mathbb{Q}}_{\ell })$
, because the complement
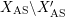 $X_{\text{AS}}\backslash X_{\text{AS}}^{\prime }$
consists of one point. The curve
$X_{\text{AS}}\backslash X_{\text{AS}}^{\prime }$
consists of one point. The curve
![]() $X_{\text{AS}}^{\prime }$
is a finite etale Galois covering of
$X_{\text{AS}}^{\prime }$
is a finite etale Galois covering of
![]() $\mathbb{A}^{1}$
with a Galois group
$\mathbb{A}^{1}$
with a Galois group
![]() $k$
by
$k$
by
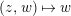 $(z,w)\mapsto w$
. For
$(z,w)\mapsto w$
. For
![]() $\unicode[STIX]{x1D713}\in k^{\vee }$
, let
$\unicode[STIX]{x1D713}\in k^{\vee }$
, let
![]() ${\mathcal{L}}_{2,\unicode[STIX]{x1D713}}$
be the smooth
${\mathcal{L}}_{2,\unicode[STIX]{x1D713}}$
be the smooth
![]() $\overline{\mathbb{Q}}_{\ell }$
-sheaf on
$\overline{\mathbb{Q}}_{\ell }$
-sheaf on
![]() $\mathbb{A}^{1}$
defined by the covering
$\mathbb{A}^{1}$
defined by the covering
![]() $X_{\text{AS}}^{\prime }$
and
$X_{\text{AS}}^{\prime }$
and
![]() $\unicode[STIX]{x1D713}$
. Then, we have
$\unicode[STIX]{x1D713}$
. Then, we have
 $$\begin{eqnarray}H_{c}^{1}(X_{\text{AS}}^{\prime },\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}}H_{c}^{1}(\mathbb{A}^{1},{\mathcal{L}}_{2,\unicode[STIX]{x1D713}})\end{eqnarray}$$
$$\begin{eqnarray}H_{c}^{1}(X_{\text{AS}}^{\prime },\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}}H_{c}^{1}(\mathbb{A}^{1},{\mathcal{L}}_{2,\unicode[STIX]{x1D713}})\end{eqnarray}$$
as
![]() $\overline{\mathbb{Q}}_{\ell }[k]$
-modules. By Lemma 7.4 and the Grothendieck–Ogg–Shafarevich formula, we have
$\overline{\mathbb{Q}}_{\ell }[k]$
-modules. By Lemma 7.4 and the Grothendieck–Ogg–Shafarevich formula, we have
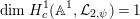 $$\begin{eqnarray}\dim H_{c}^{1}(\mathbb{A}^{1},{\mathcal{L}}_{2,\unicode[STIX]{x1D713}})=1\end{eqnarray}$$
$$\begin{eqnarray}\dim H_{c}^{1}(\mathbb{A}^{1},{\mathcal{L}}_{2,\unicode[STIX]{x1D713}})=1\end{eqnarray}$$
and
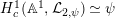 $H_{c}^{1}(\mathbb{A}^{1},{\mathcal{L}}_{2,\unicode[STIX]{x1D713}})\simeq \unicode[STIX]{x1D713}$
as
$H_{c}^{1}(\mathbb{A}^{1},{\mathcal{L}}_{2,\unicode[STIX]{x1D713}})\simeq \unicode[STIX]{x1D713}$
as
![]() $\overline{\mathbb{Q}}_{\ell }[k]$
-modules for
$\overline{\mathbb{Q}}_{\ell }[k]$
-modules for
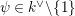 $\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}$
. Hence, the first assertion follows.
$\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}$
. Hence, the first assertion follows.
The second assertion follows from the fact that
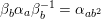 $\unicode[STIX]{x1D6FD}_{b}\unicode[STIX]{x1D6FC}_{a}\unicode[STIX]{x1D6FD}_{b}^{-1}=\unicode[STIX]{x1D6FC}_{ab^{2}}$
for
$\unicode[STIX]{x1D6FD}_{b}\unicode[STIX]{x1D6FC}_{a}\unicode[STIX]{x1D6FD}_{b}^{-1}=\unicode[STIX]{x1D6FC}_{ab^{2}}$
for
![]() $a\in k$
and
$a\in k$
and
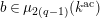 $b\in \unicode[STIX]{x1D707}_{2(q-1)}(k^{\text{ac}})$
. The assertion
$b\in \unicode[STIX]{x1D707}_{2(q-1)}(k^{\text{ac}})$
. The assertion
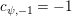 $c_{\unicode[STIX]{x1D713},-1}=-1$
follows from the Lefschetz trace formula.◻
$c_{\unicode[STIX]{x1D713},-1}=-1$
follows from the Lefschetz trace formula.◻
We put
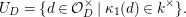 $$\begin{eqnarray}U_{D}=\{d\in {\mathcal{O}}_{D}^{\times }\mid \unicode[STIX]{x1D705}_{1}(d)\in k^{\times }\}.\end{eqnarray}$$
$$\begin{eqnarray}U_{D}=\{d\in {\mathcal{O}}_{D}^{\times }\mid \unicode[STIX]{x1D705}_{1}(d)\in k^{\times }\}.\end{eqnarray}$$
We take
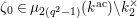 $\unicode[STIX]{x1D701}_{0}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})\backslash k_{2}^{\times }$
. Let
$\unicode[STIX]{x1D701}_{0}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})\backslash k_{2}^{\times }$
. Let
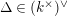 $\unicode[STIX]{x1D6E5}\in (k^{\times })^{\vee }$
be the character defined by
$\unicode[STIX]{x1D6E5}\in (k^{\times })^{\vee }$
be the character defined by
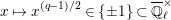 $$\begin{eqnarray}x\mapsto x^{(q-1)/2}\in \{\pm 1\}\subset \overline{\mathbb{Q}}_{\ell }^{\times }\end{eqnarray}$$
$$\begin{eqnarray}x\mapsto x^{(q-1)/2}\in \{\pm 1\}\subset \overline{\mathbb{Q}}_{\ell }^{\times }\end{eqnarray}$$
for
![]() $x\in k^{\times }$
. If
$x\in k^{\times }$
. If
![]() $q$
is odd, we put
$q$
is odd, we put
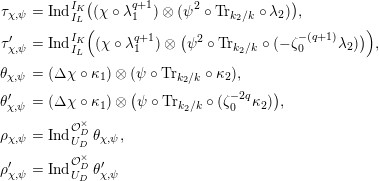 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}} & = & \displaystyle \text{Ind}_{I_{L}}^{I_{K}}((\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D706}_{1}^{q+1})\otimes (\unicode[STIX]{x1D713}^{2}\circ \text{Tr}_{k_{2}/k}\circ \unicode[STIX]{x1D706}_{2})),\nonumber\\ \displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime } & = & \displaystyle \text{Ind}_{I_{L}}^{I_{K}}\Bigl((\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D706}_{1}^{q+1})\otimes (\unicode[STIX]{x1D713}^{2}\circ \text{Tr}_{k_{2}/k}\circ (-\unicode[STIX]{x1D701}_{0}^{-(q+1)}\unicode[STIX]{x1D706}_{2}))\Bigr),\nonumber\\ \displaystyle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}} & = & \displaystyle (\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D705}_{1})\otimes (\unicode[STIX]{x1D713}\circ \text{Tr}_{k_{2}/k}\circ \unicode[STIX]{x1D705}_{2}),\nonumber\\ \displaystyle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime } & = & \displaystyle (\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D705}_{1})\otimes (\unicode[STIX]{x1D713}\circ \text{Tr}_{k_{2}/k}\circ (\unicode[STIX]{x1D701}_{0}^{-2q}\unicode[STIX]{x1D705}_{2})),\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}} & = & \displaystyle \text{Ind}_{U_{D}}^{{\mathcal{O}}_{D}^{\times }}\,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}},\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime } & = & \displaystyle \text{Ind}_{U_{D}}^{{\mathcal{O}}_{D}^{\times }}\,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}} & = & \displaystyle \text{Ind}_{I_{L}}^{I_{K}}((\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D706}_{1}^{q+1})\otimes (\unicode[STIX]{x1D713}^{2}\circ \text{Tr}_{k_{2}/k}\circ \unicode[STIX]{x1D706}_{2})),\nonumber\\ \displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime } & = & \displaystyle \text{Ind}_{I_{L}}^{I_{K}}\Bigl((\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D706}_{1}^{q+1})\otimes (\unicode[STIX]{x1D713}^{2}\circ \text{Tr}_{k_{2}/k}\circ (-\unicode[STIX]{x1D701}_{0}^{-(q+1)}\unicode[STIX]{x1D706}_{2}))\Bigr),\nonumber\\ \displaystyle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}} & = & \displaystyle (\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D705}_{1})\otimes (\unicode[STIX]{x1D713}\circ \text{Tr}_{k_{2}/k}\circ \unicode[STIX]{x1D705}_{2}),\nonumber\\ \displaystyle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime } & = & \displaystyle (\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D705}_{1})\otimes (\unicode[STIX]{x1D713}\circ \text{Tr}_{k_{2}/k}\circ (\unicode[STIX]{x1D701}_{0}^{-2q}\unicode[STIX]{x1D705}_{2})),\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}} & = & \displaystyle \text{Ind}_{U_{D}}^{{\mathcal{O}}_{D}^{\times }}\,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}},\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime } & = & \displaystyle \text{Ind}_{U_{D}}^{{\mathcal{O}}_{D}^{\times }}\,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }\nonumber\end{eqnarray}$$
for
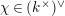 $\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }$
and
$\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }$
and
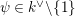 $\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}$
. We note that
$\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}$
. We note that
 $$\begin{eqnarray}\dim \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}=\dim \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }=q+1.\end{eqnarray}$$
$$\begin{eqnarray}\dim \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}=\dim \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }=q+1.\end{eqnarray}$$
For different
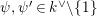 $\unicode[STIX]{x1D713},\unicode[STIX]{x1D713}^{\prime }\in k^{\vee }\backslash \{1\}$
, we can check that
$\unicode[STIX]{x1D713},\unicode[STIX]{x1D713}^{\prime }\in k^{\vee }\backslash \{1\}$
, we can check that
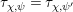 $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}^{\prime }}$
if and only if
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}^{\prime }}$
if and only if
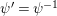 $\unicode[STIX]{x1D713}^{\prime }=\unicode[STIX]{x1D713}^{-1}$
, and
$\unicode[STIX]{x1D713}^{\prime }=\unicode[STIX]{x1D713}^{-1}$
, and
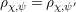 $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}^{\prime }}$
if and only if
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}^{\prime }}$
if and only if
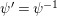 $\unicode[STIX]{x1D713}^{\prime }=\unicode[STIX]{x1D713}^{-1}$
. Similar conditions hold also for
$\unicode[STIX]{x1D713}^{\prime }=\unicode[STIX]{x1D713}^{-1}$
. Similar conditions hold also for
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }$
and
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }$
and
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }$
. We define an equivalence relation
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }$
. We define an equivalence relation
![]() ${\sim}$
on
${\sim}$
on
![]() $k^{\vee }\backslash \{1\}$
by
$k^{\vee }\backslash \{1\}$
by
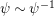 $\unicode[STIX]{x1D713}\sim \unicode[STIX]{x1D713}^{-1}$
. We put
$\unicode[STIX]{x1D713}\sim \unicode[STIX]{x1D713}^{-1}$
. We put
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}},\qquad \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }\otimes \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}},\qquad \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }\otimes \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }\end{eqnarray}$$
for
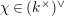 $\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }$
and
$\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }$
and
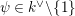 $\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}$
.
$\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}$
.
Proposition 7.6. We assume that
![]() $q$
is odd. Then, we have an isomorphism
$q$
is odd. Then, we have an isomorphism
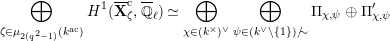 $$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\bigoplus _{\unicode[STIX]{x1D713}\in (k^{\vee }\backslash \{1\})/\!\sim }\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}\oplus \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\bigoplus _{\unicode[STIX]{x1D713}\in (k^{\vee }\backslash \{1\})/\!\sim }\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}\oplus \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }\end{eqnarray}$$
as representations of
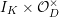 $I_{K}\times {\mathcal{O}}_{D}^{\times }$
.
$I_{K}\times {\mathcal{O}}_{D}^{\times }$
.
Proof. The actions of
![]() $I_{L}$
and
$I_{L}$
and
![]() $U_{D}$
on
$U_{D}$
on
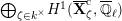 $\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })$
factor through
$\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })$
factor through
![]() $k^{\times }\times k$
by Proposition 5.4 and Corollary 6.5. On the other hand, the action of
$k^{\times }\times k$
by Proposition 5.4 and Corollary 6.5. On the other hand, the action of
![]() $k^{\times }\times k$
on
$k^{\times }\times k$
on
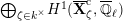 $\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })$
is induced from the action of
$\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })$
is induced from the action of
![]() $\{1\}\times k$
on
$\{1\}\times k$
on
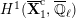 $H^{1}(\overline{\mathbf{X}}_{1}^{\text{c}},\overline{\mathbb{Q}}_{\ell })$
. Hence, we have
$H^{1}(\overline{\mathbf{X}}_{1}^{\text{c}},\overline{\mathbb{Q}}_{\ell })$
. Hence, we have
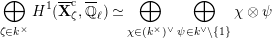 $$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}}\unicode[STIX]{x1D712}\otimes \unicode[STIX]{x1D713}\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}}\unicode[STIX]{x1D712}\otimes \unicode[STIX]{x1D713}\end{eqnarray}$$
as representations of
![]() $k^{\times }\times k$
by Lemma 7.5.1. Therefore, we have an isomorphism
$k^{\times }\times k$
by Lemma 7.5.1. Therefore, we have an isomorphism
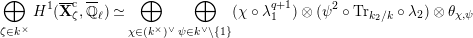 $$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}}(\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D706}_{1}^{q+1})\otimes (\unicode[STIX]{x1D713}^{2}\circ \text{Tr}_{k_{2}/k}\circ \unicode[STIX]{x1D706}_{2})\otimes \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}}(\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D706}_{1}^{q+1})\otimes (\unicode[STIX]{x1D713}^{2}\circ \text{Tr}_{k_{2}/k}\circ \unicode[STIX]{x1D706}_{2})\otimes \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}\end{eqnarray}$$
as representations of
 $I_{L}\times U_{D}$
by Proposition 5.4, Corollary 6.5 and Lemma 7.5.2. Inducing this representation from
$I_{L}\times U_{D}$
by Proposition 5.4, Corollary 6.5 and Lemma 7.5.2. Inducing this representation from
![]() $U_{D}$
to
$U_{D}$
to
![]() ${\mathcal{O}}_{D}^{\times }$
, we obtain an isomorphism
${\mathcal{O}}_{D}^{\times }$
, we obtain an isomorphism
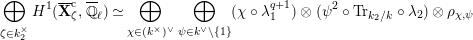 $$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in k_{2}^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}}(\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D706}_{1}^{q+1})\otimes (\unicode[STIX]{x1D713}^{2}\circ \text{Tr}_{k_{2}/k}\circ \unicode[STIX]{x1D706}_{2})\otimes \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in k_{2}^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\bigoplus _{\unicode[STIX]{x1D713}\in k^{\vee }\backslash \{1\}}(\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D706}_{1}^{q+1})\otimes (\unicode[STIX]{x1D713}^{2}\circ \text{Tr}_{k_{2}/k}\circ \unicode[STIX]{x1D706}_{2})\otimes \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}\end{eqnarray}$$
as representations of
 $I_{L}\times {\mathcal{O}}_{D}^{\times }$
. On the left-hand side of this isomorphism, we have an action of
$I_{L}\times {\mathcal{O}}_{D}^{\times }$
. On the left-hand side of this isomorphism, we have an action of
![]() $I_{K}$
that commutes with the action of
$I_{K}$
that commutes with the action of
![]() ${\mathcal{O}}_{D}^{\times }$
. Hence, we have
${\mathcal{O}}_{D}^{\times }$
. Hence, we have
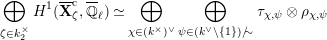 $$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in k_{2}^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\bigoplus _{\unicode[STIX]{x1D713}\in (k^{\vee }\backslash \{1\})/\!\sim }\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in k_{2}^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\bigoplus _{\unicode[STIX]{x1D713}\in (k^{\vee }\backslash \{1\})/\!\sim }\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}\otimes \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}\end{eqnarray}$$
as representations of
 $I_{K}\times {\mathcal{O}}_{D}^{\times }$
. By similar arguments, we have
$I_{K}\times {\mathcal{O}}_{D}^{\times }$
. By similar arguments, we have
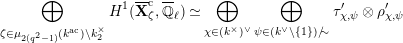 $$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})\backslash k_{2}^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\bigoplus _{\unicode[STIX]{x1D713}\in (k^{\vee }\backslash \{1\})/\!\sim }\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }\otimes \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})\backslash k_{2}^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\bigoplus _{\unicode[STIX]{x1D713}\in (k^{\vee }\backslash \{1\})/\!\sim }\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }\otimes \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }\end{eqnarray}$$
as representations of
 $I_{K}\times {\mathcal{O}}_{D}^{\times }$
. Therefore, we have the isomorphism in the assertion.◻
$I_{K}\times {\mathcal{O}}_{D}^{\times }$
. Therefore, we have the isomorphism in the assertion.◻
Let
![]() $E$
and
$E$
and
![]() $Q$
be as in Section 6.2.2. Let
$Q$
be as in Section 6.2.2. Let
![]() $Z\subset Q$
be the subgroup consisting of
$Z\subset Q$
be the subgroup consisting of
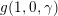 $g(1,0,\unicode[STIX]{x1D6FE})$
with
$g(1,0,\unicode[STIX]{x1D6FE})$
with
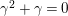 $\unicode[STIX]{x1D6FE}^{2}+\unicode[STIX]{x1D6FE}=0$
, and let
$\unicode[STIX]{x1D6FE}^{2}+\unicode[STIX]{x1D6FE}=0$
, and let
![]() $\unicode[STIX]{x1D719}$
be the unique nontrivial character of
$\unicode[STIX]{x1D719}$
be the unique nontrivial character of
![]() $Z$
. By [Reference Bushnell and HenniartBH, Lemma 22.2], there exists a unique irreducible two-dimensional representation
$Z$
. By [Reference Bushnell and HenniartBH, Lemma 22.2], there exists a unique irreducible two-dimensional representation
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $Q$
such that
$Q$
such that
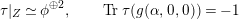 $$\begin{eqnarray}\unicode[STIX]{x1D70F}|_{Z}\simeq \unicode[STIX]{x1D719}^{\oplus 2},\qquad \text{Tr}\,\unicode[STIX]{x1D70F}(g(\unicode[STIX]{x1D6FC},0,0))=-1\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}|_{Z}\simeq \unicode[STIX]{x1D719}^{\oplus 2},\qquad \text{Tr}\,\unicode[STIX]{x1D70F}(g(\unicode[STIX]{x1D6FC},0,0))=-1\end{eqnarray}$$
for
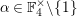 $\unicode[STIX]{x1D6FC}\in \mathbb{F}_{4}^{\times }\backslash \{1\}$
. Then, it is easily checked that the determinant character of
$\unicode[STIX]{x1D6FC}\in \mathbb{F}_{4}^{\times }\backslash \{1\}$
. Then, it is easily checked that the determinant character of
![]() $\unicode[STIX]{x1D70F}$
is trivial. Note that every two-dimensional irreducible representation of
$\unicode[STIX]{x1D70F}$
is trivial. Note that every two-dimensional irreducible representation of
![]() $Q$
has a form
$Q$
has a form
![]() $\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D712}$
with
$\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D712}$
with
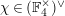 $\unicode[STIX]{x1D712}\in (\mathbb{F}_{4}^{\times })^{\vee }$
, where we consider
$\unicode[STIX]{x1D712}\in (\mathbb{F}_{4}^{\times })^{\vee }$
, where we consider
![]() $\unicode[STIX]{x1D712}$
as a character of
$\unicode[STIX]{x1D712}$
as a character of
![]() $Q$
by
$Q$
by
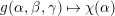 $g(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})\mapsto \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC})$
.
$g(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})\mapsto \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC})$
.
Lemma 7.7. The
![]() $Q$
-representation
$Q$
-representation
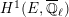 $H^{1}(E,\overline{\mathbb{Q}}_{\ell })$
is isomorphic to
$H^{1}(E,\overline{\mathbb{Q}}_{\ell })$
is isomorphic to
![]() $\unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70F}$
.
Proof. The
![]() $Q$
-representation
$Q$
-representation
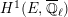 $H^{1}(E,\overline{\mathbb{Q}}_{\ell })$
satisfies (7.4) by Lemma 7.1. Hence, the assertion follows.◻
$H^{1}(E,\overline{\mathbb{Q}}_{\ell })$
satisfies (7.4) by Lemma 7.1. Hence, the assertion follows.◻
Let
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime }}$
be the representation of
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime }}$
be the representation of
![]() $W_{K}$
induced from the
$W_{K}$
induced from the
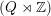 $(Q\rtimes \mathbb{Z})$
-representation
$(Q\rtimes \mathbb{Z})$
-representation
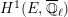 $H^{1}(E,\overline{\mathbb{Q}}_{\ell })$
by
$H^{1}(E,\overline{\mathbb{Q}}_{\ell })$
by
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D701}^{\prime }}$
. Then, the restriction to
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D701}^{\prime }}$
. Then, the restriction to
![]() $I_{K}$
of
$I_{K}$
of
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime }}$
is isomorphic to the representation induced from
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime }}$
is isomorphic to the representation induced from
![]() $\unicode[STIX]{x1D70F}$
by Lemma 7.7.
$\unicode[STIX]{x1D70F}$
by Lemma 7.7.
We say that a continuous two-dimensional irreducible representation
![]() $V$
of
$V$
of
![]() $W_{K}$
over
$W_{K}$
over
![]() $\overline{\mathbb{Q}}_{\ell }$
is primitive, if there is no pair of a quadratic extension
$\overline{\mathbb{Q}}_{\ell }$
is primitive, if there is no pair of a quadratic extension
![]() $K^{\prime }$
and a continuous character
$K^{\prime }$
and a continuous character
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $W_{K^{\prime }}$
such that
$W_{K^{\prime }}$
such that
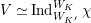 $V\simeq \text{Ind}_{W_{K^{\prime }}}^{W_{K}}\,\unicode[STIX]{x1D712}$
.
$V\simeq \text{Ind}_{W_{K^{\prime }}}^{W_{K}}\,\unicode[STIX]{x1D712}$
.
Lemma 7.8. The representation
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime }}$
is primitive of Artin conductor
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime }}$
is primitive of Artin conductor
![]() $3$
.
$3$
.
Proof. We use the notations in the proof of Lemma 6.11. The element
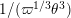 $1/(\unicode[STIX]{x1D71B}^{1/3}\unicode[STIX]{x1D703}^{3})$
is a uniformizer of
$1/(\unicode[STIX]{x1D71B}^{1/3}\unicode[STIX]{x1D703}^{3})$
is a uniformizer of
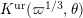 $K^{\text{ur}}(\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})$
. For
$K^{\text{ur}}(\unicode[STIX]{x1D71B}^{1/3},\unicode[STIX]{x1D703})$
. For
![]() $\unicode[STIX]{x1D70E}\in I_{K}$
, we can show that
$\unicode[STIX]{x1D70E}\in I_{K}$
, we can show that
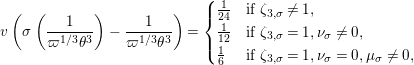 $$\begin{eqnarray}v\left(\unicode[STIX]{x1D70E}\left({\displaystyle \frac{1}{\unicode[STIX]{x1D71B}^{1/3}\unicode[STIX]{x1D703}^{3}}}\right)-{\displaystyle \frac{1}{\unicode[STIX]{x1D71B}^{1/3}\unicode[STIX]{x1D703}^{3}}}\right)=\left\{\begin{array}{@{}ll@{}}{\textstyle \frac{1}{24}}\quad & \text{if }\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}\neq 1,\\ {\textstyle \frac{1}{12}}\quad & \text{if }\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}=1,\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}\neq 0,\\ {\textstyle \frac{1}{6}}\quad & \text{if }\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}=1,\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}=0,\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}\neq 0,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}v\left(\unicode[STIX]{x1D70E}\left({\displaystyle \frac{1}{\unicode[STIX]{x1D71B}^{1/3}\unicode[STIX]{x1D703}^{3}}}\right)-{\displaystyle \frac{1}{\unicode[STIX]{x1D71B}^{1/3}\unicode[STIX]{x1D703}^{3}}}\right)=\left\{\begin{array}{@{}ll@{}}{\textstyle \frac{1}{24}}\quad & \text{if }\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}\neq 1,\\ {\textstyle \frac{1}{12}}\quad & \text{if }\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}=1,\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}\neq 0,\\ {\textstyle \frac{1}{6}}\quad & \text{if }\unicode[STIX]{x1D701}_{3,\unicode[STIX]{x1D70E}}=1,\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D70E}}=0,\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D70E}}\neq 0,\end{array}\right.\end{eqnarray}$$
using
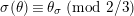 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\equiv \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}}\;(\text{mod}~2/3)$
. The claim on the Artin conductor follows from this.
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D703})\equiv \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70E}}\;(\text{mod}~2/3)$
. The claim on the Artin conductor follows from this.
The unique index-
![]() $2$
subgroup of
$2$
subgroup of
![]() $Q\rtimes \mathbb{Z}$
is
$Q\rtimes \mathbb{Z}$
is
![]() $Q\rtimes 2\mathbb{Z}$
, because
$Q\rtimes 2\mathbb{Z}$
, because
![]() $Q$
has no index-
$Q$
has no index-
![]() $2$
subgroup. Hence, if
$2$
subgroup. Hence, if
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime }}$
is not primitive, it is induced from a character of
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime }}$
is not primitive, it is induced from a character of
![]() $W_{K_{2}}$
. However, this is impossible, because the restriction of
$W_{K_{2}}$
. However, this is impossible, because the restriction of
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime }}$
to
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime }}$
to
![]() $W_{K_{2}}$
is irreducible.◻
$W_{K_{2}}$
is irreducible.◻
We define a character
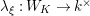 $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709}}:W_{K}\rightarrow k^{\times }$
by
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709}}:W_{K}\rightarrow k^{\times }$
by
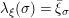 $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70E})=\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}$
. We put
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D70E})=\bar{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D70E}}$
. We put
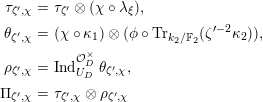 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}} & = & \displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime }}\otimes (\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709}}),\nonumber\\ \displaystyle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}} & = & \displaystyle (\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D705}_{1})\otimes (\unicode[STIX]{x1D719}\circ \text{Tr}_{k_{2}/\mathbb{F}_{2}}(\unicode[STIX]{x1D701}^{\prime -2}\unicode[STIX]{x1D705}_{2})),\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}} & = & \displaystyle \text{Ind}_{U_{D}}^{{\mathcal{O}}_{D}^{\times }}\,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}},\nonumber\\ \displaystyle \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}} & = & \displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}}\otimes \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}} & = & \displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime }}\otimes (\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D706}_{\unicode[STIX]{x1D709}}),\nonumber\\ \displaystyle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}} & = & \displaystyle (\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D705}_{1})\otimes (\unicode[STIX]{x1D719}\circ \text{Tr}_{k_{2}/\mathbb{F}_{2}}(\unicode[STIX]{x1D701}^{\prime -2}\unicode[STIX]{x1D705}_{2})),\nonumber\\ \displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}} & = & \displaystyle \text{Ind}_{U_{D}}^{{\mathcal{O}}_{D}^{\times }}\,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}},\nonumber\\ \displaystyle \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}} & = & \displaystyle \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}}\otimes \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}}\nonumber\end{eqnarray}$$
for
![]() $\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
and
$\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
and
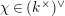 $\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }$
. In the following, we consider
$\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }$
. In the following, we consider
![]() $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}}$
as a representation of
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}}$
as a representation of
![]() $I_{K}$
.
$I_{K}$
.
Proposition 7.9. We assume that
![]() $q$
is even. Let
$q$
is even. Let
![]() $\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
. Then, we have an isomorphism
$\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
. Then, we have an isomorphism
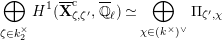 $$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in k_{2}^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}}\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in k_{2}^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}}\end{eqnarray}$$
as representations of
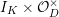 $I_{K}\times {\mathcal{O}}_{D}^{\times }$
.
$I_{K}\times {\mathcal{O}}_{D}^{\times }$
.
Proof. The actions of
![]() $I_{K}$
and
$I_{K}$
and
![]() $U_{D}$
on
$U_{D}$
on
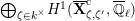 $\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}^{\text{c}},\overline{\mathbb{Q}}_{\ell })$
factor through
$\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}^{\text{c}},\overline{\mathbb{Q}}_{\ell })$
factor through
![]() $Q\times k^{\times }$
by Propositions 5.4 and 6.12. On the other hand, the action of
$Q\times k^{\times }$
by Propositions 5.4 and 6.12. On the other hand, the action of
![]() $Q\times k^{\times }$
on
$Q\times k^{\times }$
on
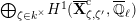 $\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}^{\text{c}},\overline{\mathbb{Q}}_{\ell })$
is induced from the action of
$\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}^{\text{c}},\overline{\mathbb{Q}}_{\ell })$
is induced from the action of
![]() $Q$
on
$Q$
on
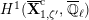 $H^{1}(\overline{\mathbf{X}}_{1,\unicode[STIX]{x1D701}^{\prime }}^{\text{c}},\overline{\mathbb{Q}}_{\ell })$
. Hence, we have an isomorphism
$H^{1}(\overline{\mathbf{X}}_{1,\unicode[STIX]{x1D701}^{\prime }}^{\text{c}},\overline{\mathbb{Q}}_{\ell })$
. Hence, we have an isomorphism
 $$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D712}\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\unicode[STIX]{x1D70F}\otimes \unicode[STIX]{x1D712}\end{eqnarray}$$
as representations of
![]() $Q\times k^{\times }$
. Therefore, we have an isomorphism
$Q\times k^{\times }$
. Therefore, we have an isomorphism
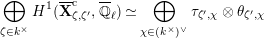 $$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}}\otimes \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}}\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D701}\in k^{\times }}H^{1}(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}^{\text{c}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}}\otimes \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}}\end{eqnarray}$$
as representations of
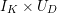 $I_{K}\times U_{D}$
by Propositions 5.4 and 6.12. Inducing this representation from
$I_{K}\times U_{D}$
by Propositions 5.4 and 6.12. Inducing this representation from
![]() $U_{D}$
to
$U_{D}$
to
![]() ${\mathcal{O}}_{D}^{\times }$
, we obtain the isomorphism in the assertion.◻
${\mathcal{O}}_{D}^{\times }$
, we obtain the isomorphism in the assertion.◻
7.2 Genus calculation
Lemma 7.10. We have
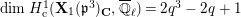 $\dim H_{\text{c}}^{1}(\mathbf{X}_{1}(\mathfrak{p}^{3})_{\mathbf{C}},\overline{\mathbb{Q}}_{\ell })=2q^{3}-2q+1$
.
$\dim H_{\text{c}}^{1}(\mathbf{X}_{1}(\mathfrak{p}^{3})_{\mathbf{C}},\overline{\mathbb{Q}}_{\ell })=2q^{3}-2q+1$
.
Proof. It suffices to show that
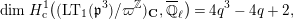 $$\begin{eqnarray}\dim H_{\text{c}}^{1}((\text{LT}_{1}(\mathfrak{p}^{3})/\unicode[STIX]{x1D71B}^{\mathbb{Z}})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell })=4q^{3}-4q+2,\end{eqnarray}$$
$$\begin{eqnarray}\dim H_{\text{c}}^{1}((\text{LT}_{1}(\mathfrak{p}^{3})/\unicode[STIX]{x1D71B}^{\mathbb{Z}})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell })=4q^{3}-4q+2,\end{eqnarray}$$
because we have
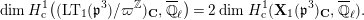 $$\begin{eqnarray}\dim H_{\text{c}}^{1}((\text{LT}_{1}(\mathfrak{p}^{3})/\unicode[STIX]{x1D71B}^{\mathbb{Z}})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell })=2\dim H_{\text{c}}^{1}(\mathbf{X}_{1}(\mathfrak{p}^{3})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell }).\end{eqnarray}$$
$$\begin{eqnarray}\dim H_{\text{c}}^{1}((\text{LT}_{1}(\mathfrak{p}^{3})/\unicode[STIX]{x1D71B}^{\mathbb{Z}})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell })=2\dim H_{\text{c}}^{1}(\mathbf{X}_{1}(\mathfrak{p}^{3})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell }).\end{eqnarray}$$
For an irreducible smooth representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
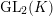 $\text{GL}_{2}(K)$
, we write
$\text{GL}_{2}(K)$
, we write
![]() $c(\unicode[STIX]{x1D70B})$
for the conductor of
$c(\unicode[STIX]{x1D70B})$
for the conductor of
![]() $\unicode[STIX]{x1D70B}$
. By Proposition 2.1, we have
$\unicode[STIX]{x1D70B}$
. By Proposition 2.1, we have
 $$\begin{eqnarray}H_{\text{c}}^{1}((\text{LT}_{1}(\mathfrak{p}^{3})/\unicode[STIX]{x1D71B}^{\mathbb{Z}})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70B}^{K_{1}(\mathfrak{p}^{3})})^{\oplus 2\dim \text{LJ}(\unicode[STIX]{x1D70B})}\oplus \bigoplus _{\unicode[STIX]{x1D712}}(\text{St}\otimes \unicode[STIX]{x1D712})^{K_{1}(\mathfrak{p}^{3})},\end{eqnarray}$$
$$\begin{eqnarray}H_{\text{c}}^{1}((\text{LT}_{1}(\mathfrak{p}^{3})/\unicode[STIX]{x1D71B}^{\mathbb{Z}})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell })\simeq \bigoplus _{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D70B}^{K_{1}(\mathfrak{p}^{3})})^{\oplus 2\dim \text{LJ}(\unicode[STIX]{x1D70B})}\oplus \bigoplus _{\unicode[STIX]{x1D712}}(\text{St}\otimes \unicode[STIX]{x1D712})^{K_{1}(\mathfrak{p}^{3})},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70B}$
runs through irreducible cuspidal representations of
$\unicode[STIX]{x1D70B}$
runs through irreducible cuspidal representations of
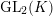 $\text{GL}_{2}(K)$
such that
$\text{GL}_{2}(K)$
such that
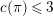 $c(\unicode[STIX]{x1D70B})\leqslant 3$
and
$c(\unicode[STIX]{x1D70B})\leqslant 3$
and
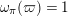 $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D71B})=1$
, and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D71B})=1$
, and
![]() $\unicode[STIX]{x1D712}$
runs through characters of
$\unicode[STIX]{x1D712}$
runs through characters of
![]() $K^{\times }$
such that
$K^{\times }$
such that
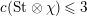 $c(\text{St}\otimes \unicode[STIX]{x1D712})\leqslant 3$
and
$c(\text{St}\otimes \unicode[STIX]{x1D712})\leqslant 3$
and
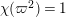 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{2})=1$
. We have the following list of discrete series representations
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{2})=1$
. We have the following list of discrete series representations
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
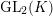 $\text{GL}_{2}(K)$
such that
$\text{GL}_{2}(K)$
such that
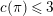 $c(\unicode[STIX]{x1D70B})\leqslant 3$
and
$c(\unicode[STIX]{x1D70B})\leqslant 3$
and
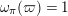 $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D71B})=1$
.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D71B})=1$
.
-
(1)
 $\unicode[STIX]{x1D70B}\simeq \text{St}\otimes \unicode[STIX]{x1D712}$
for an unramified character
$\unicode[STIX]{x1D70B}\simeq \text{St}\otimes \unicode[STIX]{x1D712}$
for an unramified character
 $\unicode[STIX]{x1D712}:K^{\times }\rightarrow \overline{\mathbb{Q}}_{\ell }^{\times }$
such that
$\unicode[STIX]{x1D712}:K^{\times }\rightarrow \overline{\mathbb{Q}}_{\ell }^{\times }$
such that
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{2})=1$
. Then,
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{2})=1$
. Then,
 $c(\unicode[STIX]{x1D70B})=1$
and
$c(\unicode[STIX]{x1D70B})=1$
and
 $\dim \text{LJ}(\unicode[STIX]{x1D70B})=1$
. There are two such representations.
$\dim \text{LJ}(\unicode[STIX]{x1D70B})=1$
. There are two such representations. -
(2)
 $\unicode[STIX]{x1D70B}\simeq \text{St}\otimes \unicode[STIX]{x1D712}$
for a tamely ramified character
$\unicode[STIX]{x1D70B}\simeq \text{St}\otimes \unicode[STIX]{x1D712}$
for a tamely ramified character
 $\unicode[STIX]{x1D712}:K^{\times }\rightarrow \overline{\mathbb{Q}}_{\ell }^{\times }$
that is not unramified and satisfies
$\unicode[STIX]{x1D712}:K^{\times }\rightarrow \overline{\mathbb{Q}}_{\ell }^{\times }$
that is not unramified and satisfies
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{2})=1$
. Then,
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B}^{2})=1$
. Then,
 $c(\unicode[STIX]{x1D70B})=2$
and
$c(\unicode[STIX]{x1D70B})=2$
and
 $\dim \text{LJ}(\unicode[STIX]{x1D70B})=1$
. There are
$\dim \text{LJ}(\unicode[STIX]{x1D70B})=1$
. There are
 $2(q-2)$
such representations.
$2(q-2)$
such representations. -
(3)
 $\unicode[STIX]{x1D70B}\simeq \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D712}}$
, in the notation of [Reference Bushnell and HenniartBH, 19.1], for a character
$\unicode[STIX]{x1D70B}\simeq \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D712}}$
, in the notation of [Reference Bushnell and HenniartBH, 19.1], for a character
 $\unicode[STIX]{x1D712}:K_{2}^{\times }\rightarrow \overline{\mathbb{Q}}_{\ell }^{\times }$
of level zero such that
$\unicode[STIX]{x1D712}:K_{2}^{\times }\rightarrow \overline{\mathbb{Q}}_{\ell }^{\times }$
of level zero such that
 $\unicode[STIX]{x1D712}$
does not factor through
$\unicode[STIX]{x1D712}$
does not factor through
 $\text{Nr}_{K_{2}/K}$
and
$\text{Nr}_{K_{2}/K}$
and
 $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B})=1$
. Then,
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D71B})=1$
. Then,
 $c(\unicode[STIX]{x1D70B})=2$
and
$c(\unicode[STIX]{x1D70B})=2$
and
 $\dim \text{LJ}(\unicode[STIX]{x1D70B})=2$
. There are
$\dim \text{LJ}(\unicode[STIX]{x1D70B})=2$
. There are
 $q(q-1)/2$
such representations.
$q(q-1)/2$
such representations. -
(4) The cuspidal representations
 $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
 $\text{GL}_{2}(K)$
such that
$\text{GL}_{2}(K)$
such that
 $c(\unicode[STIX]{x1D70B})=3$
and
$c(\unicode[STIX]{x1D70B})=3$
and
 $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D71B})=1$
. Then,
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}(\unicode[STIX]{x1D71B})=1$
. Then,
 $\dim \text{LJ}(\unicode[STIX]{x1D70B})=q+1$
by [Reference TunnellTu, Theorem 3.6]. There are
$\dim \text{LJ}(\unicode[STIX]{x1D70B})=q+1$
by [Reference TunnellTu, Theorem 3.6]. There are
 $2(q-1)^{2}$
such representations by [Reference TunnellTu, Theorem 3.9].
$2(q-1)^{2}$
such representations by [Reference TunnellTu, Theorem 3.9].
We note that
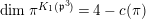 $\dim \unicode[STIX]{x1D70B}^{K_{1}(\mathfrak{p}^{3})}=4-c(\unicode[STIX]{x1D70B})$
if
$\dim \unicode[STIX]{x1D70B}^{K_{1}(\mathfrak{p}^{3})}=4-c(\unicode[STIX]{x1D70B})$
if
![]() $\unicode[STIX]{x1D70B}$
is a discrete series representation of
$\unicode[STIX]{x1D70B}$
is a discrete series representation of
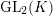 $\text{GL}_{2}(K)$
such that
$\text{GL}_{2}(K)$
such that
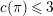 $c(\unicode[STIX]{x1D70B})\leqslant 3$
. Then, we obtain the claim by taking a summation according to the above list.◻
$c(\unicode[STIX]{x1D70B})\leqslant 3$
. Then, we obtain the claim by taking a summation according to the above list.◻
For an affinoid rigid space
![]() $X$
, a Zariski subaffinoid of
$X$
, a Zariski subaffinoid of
![]() $X$
is the inverse image of a nonempty open subscheme of
$X$
is the inverse image of a nonempty open subscheme of
![]() $\overline{X}$
under the reduction map
$\overline{X}$
under the reduction map
 $X\rightarrow \overline{X}$
.
$X\rightarrow \overline{X}$
.
Proposition 7.11. Let
![]() $W$
be a wide open rigid curve over a finite extension of
$W$
be a wide open rigid curve over a finite extension of
![]() $\widehat{K}^{\text{ur}}$
with a stable covering
$\widehat{K}^{\text{ur}}$
with a stable covering
 $\{(U_{i},U_{i}^{\text{u}})\}_{i\in I}$
. Let
$\{(U_{i},U_{i}^{\text{u}})\}_{i\in I}$
. Let
![]() $X$
be a subaffinoid space of
$X$
be a subaffinoid space of
![]() $W$
such that
$W$
such that
![]() $\overline{X}$
is a connected smooth curve with a positive genus. Then, there exists
$\overline{X}$
is a connected smooth curve with a positive genus. Then, there exists
![]() $i\in I$
such that
$i\in I$
such that
![]() $X$
is a Zariski subaffinoid of
$X$
is a Zariski subaffinoid of
![]() $U_{i}^{\text{u}}$
.
$U_{i}^{\text{u}}$
.
Proof. Assume that
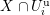 $X\cap U_{i}^{\text{u}}$
is contained in a finite union of residue classes of
$X\cap U_{i}^{\text{u}}$
is contained in a finite union of residue classes of
![]() $X$
for any
$X$
for any
![]() $i\in I$
. Then, a Zariski subaffinoid of
$i\in I$
. Then, a Zariski subaffinoid of
![]() $X$
appears in an open annulus. This is a contradiction, because
$X$
appears in an open annulus. This is a contradiction, because
![]() $\overline{X}$
has a positive genus. Hence, there exists
$\overline{X}$
has a positive genus. Hence, there exists
![]() $i^{\prime }\in I$
such that
$i^{\prime }\in I$
such that
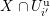 $X\cap U_{i^{\prime }}^{\text{u}}$
is not contained in any finite union of residue class of
$X\cap U_{i^{\prime }}^{\text{u}}$
is not contained in any finite union of residue class of
![]() $X$
. We fix such
$X$
. We fix such
![]() $i^{\prime }$
in the following.
$i^{\prime }$
in the following.
Then, some open irreducible subscheme of the reduction of
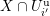 $X\cap U_{i^{\prime }}^{\text{u}}$
does not go to one point in
$X\cap U_{i^{\prime }}^{\text{u}}$
does not go to one point in
![]() $\overline{X}$
under the natural map
$\overline{X}$
under the natural map
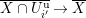 $\overline{X\cap U_{i^{\prime }}^{\text{u}}}\rightarrow \overline{X}$
. Let
$\overline{X\cap U_{i^{\prime }}^{\text{u}}}\rightarrow \overline{X}$
. Let
![]() $Y$
be the inverse image of such an open subscheme under the reduction map
$Y$
be the inverse image of such an open subscheme under the reduction map
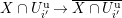 $X\cap U_{i^{\prime }}^{\text{u}}\rightarrow \overline{X\cap U_{i^{\prime }}^{\text{u}}}$
. Then, we see that
$X\cap U_{i^{\prime }}^{\text{u}}\rightarrow \overline{X\cap U_{i^{\prime }}^{\text{u}}}$
. Then, we see that
![]() $Y$
is a Zariski subaffinoid of
$Y$
is a Zariski subaffinoid of
![]() $X$
by [Reference Coleman and McMurdyCM, Lemma 2.24(i)]. Each connected component of
$X$
by [Reference Coleman and McMurdyCM, Lemma 2.24(i)]. Each connected component of
![]() $X\setminus Y$
is an open disk, and is included in
$X\setminus Y$
is an open disk, and is included in
![]() $U_{i^{\prime }}^{\text{u}}$
or
$U_{i^{\prime }}^{\text{u}}$
or
![]() $U_{i}^{\text{u}}$
for
$U_{i}^{\text{u}}$
for
![]() $i\neq i^{\prime }$
or an open annulus outside the underlying affinoids. This can be checked by applying [Reference Coleman and McMurdyCM, Corollary 2.39] to every closed disk in a connected component of
$i\neq i^{\prime }$
or an open annulus outside the underlying affinoids. This can be checked by applying [Reference Coleman and McMurdyCM, Corollary 2.39] to every closed disk in a connected component of
![]() $X\setminus Y$
. Hence,
$X\setminus Y$
. Hence,
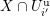 $X\cap U_{i^{\prime }}^{\text{u}}$
is a Zariski subaffinoid of
$X\cap U_{i^{\prime }}^{\text{u}}$
is a Zariski subaffinoid of
![]() $X$
. If
$X$
. If
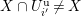 $X\cap U_{i^{\prime }}^{\text{u}}\neq X$
, then
$X\cap U_{i^{\prime }}^{\text{u}}\neq X$
, then
![]() $U_{i^{\prime }}^{\text{u}}$
is connected to an open disk in
$U_{i^{\prime }}^{\text{u}}$
is connected to an open disk in
![]() $U_{i}^{\text{u}}$
for
$U_{i}^{\text{u}}$
for
![]() $i\neq i^{\prime }$
or in an open annulus outside the underlying affinoids. This is a contradiction. Therefore, we have
$i\neq i^{\prime }$
or in an open annulus outside the underlying affinoids. This is a contradiction. Therefore, we have
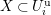 $X\subset U_{i}^{\text{u}}$
. Then, we obtain the claim by [Reference Coleman and McMurdyCM, Lemma 2.24(i)].◻
$X\subset U_{i}^{\text{u}}$
. Then, we obtain the claim by [Reference Coleman and McMurdyCM, Lemma 2.24(i)].◻
Lemma 7.12. Let
![]() $W$
be a wide open rigid curve over a finite extension of
$W$
be a wide open rigid curve over a finite extension of
![]() $\widehat{K}^{\text{ur}}$
with a stable covering. Let
$\widehat{K}^{\text{ur}}$
with a stable covering. Let
![]() $X$
be a subaffinoid space of
$X$
be a subaffinoid space of
![]() $W$
such that
$W$
such that
![]() $\overline{X}$
is a connected smooth curve with genus zero. Then, there is a basic wide open subspace of
$\overline{X}$
is a connected smooth curve with genus zero. Then, there is a basic wide open subspace of
![]() $W$
such that its underlying affinoid is
$W$
such that its underlying affinoid is
![]() $X$
.
$X$
.
Proof. We note that we have the claim if
![]() $X$
appears in an open subannulus of
$X$
appears in an open subannulus of
![]() $W$
. Let
$W$
. Let
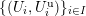 $\{(U_{i},U_{i}^{\text{u}})\}_{i\in I}$
be the stable covering of
$\{(U_{i},U_{i}^{\text{u}})\}_{i\in I}$
be the stable covering of
![]() $W$
.
$W$
.
First, we consider the case where
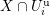 $X\cap U_{i}^{\text{u}}$
is contained in a finite union of residue classes of
$X\cap U_{i}^{\text{u}}$
is contained in a finite union of residue classes of
![]() $X$
for any
$X$
for any
![]() $i\in I$
. Then, a Zariski subaffinoid of
$i\in I$
. Then, a Zariski subaffinoid of
![]() $X$
appears in an open annulus. Further,
$X$
appears in an open annulus. Further,
![]() $X$
itself appears in the open annulus, because
$X$
itself appears in the open annulus, because
![]() $X$
is connected. Hence, we have the claim in this case.
$X$
is connected. Hence, we have the claim in this case.
Therefore, we may assume that there exists
![]() $i^{\prime }\in I$
such that
$i^{\prime }\in I$
such that
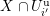 $X\cap U_{i^{\prime }}^{\text{u}}$
is not contained in any finite union of residue class of
$X\cap U_{i^{\prime }}^{\text{u}}$
is not contained in any finite union of residue class of
![]() $X$
. We fix such
$X$
. We fix such
![]() $i^{\prime }$
. By the same argument as in the proof of Proposition 7.11, we have
$i^{\prime }$
. By the same argument as in the proof of Proposition 7.11, we have
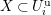 $X\subset U_{i}^{\text{u}}$
. If the image of the induced map
$X\subset U_{i}^{\text{u}}$
. If the image of the induced map
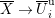 $\overline{X}\rightarrow \overline{U}_{i}^{\text{u}}$
is one point, we have the claim because
$\overline{X}\rightarrow \overline{U}_{i}^{\text{u}}$
is one point, we have the claim because
![]() $X$
appears in an open disk. Otherwise,
$X$
appears in an open disk. Otherwise,
![]() $X$
is a Zariski subaffinoid of
$X$
is a Zariski subaffinoid of
![]() $U_{i}^{\text{u}}$
, and we have the claim.◻
$U_{i}^{\text{u}}$
, and we have the claim.◻
We consider the natural level-lowering map
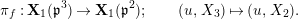 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{f}:\mathbf{X}_{1}(\mathfrak{p}^{3})\rightarrow \mathbf{X}_{1}(\mathfrak{p}^{2});\qquad (u,X_{3})\mapsto (u,X_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{f}:\mathbf{X}_{1}(\mathfrak{p}^{3})\rightarrow \mathbf{X}_{1}(\mathfrak{p}^{2});\qquad (u,X_{3})\mapsto (u,X_{2}).\end{eqnarray}$$
Lemma 7.13. The connected components of
![]() $\mathbf{W}_{1,2^{\prime }}$
,
$\mathbf{W}_{1,2^{\prime }}$
,
![]() $\mathbf{W}_{1,3^{\prime }}$
,
$\mathbf{W}_{1,3^{\prime }}$
,
![]() $\mathbf{W}_{2,1^{\prime }}$
and
$\mathbf{W}_{2,1^{\prime }}$
and
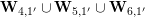 $\mathbf{W}_{4,1^{\prime }}\cup \mathbf{W}_{5,1^{\prime }}\cup \mathbf{W}_{6,1^{\prime }}$
are not open balls.
$\mathbf{W}_{4,1^{\prime }}\cup \mathbf{W}_{5,1^{\prime }}\cup \mathbf{W}_{6,1^{\prime }}$
are not open balls.
Proof. Let
![]() $\mathbf{W}_{0}^{\prime }$
be a subannulus of
$\mathbf{W}_{0}^{\prime }$
be a subannulus of
![]() $\mathbf{W}_{0}$
defined by
$\mathbf{W}_{0}$
defined by
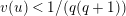 $v(u)<1/(q(q+1))$
. Then, we have
$v(u)<1/(q(q+1))$
. Then, we have
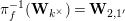 $\unicode[STIX]{x1D70B}_{f}^{-1}(\mathbf{W}_{k^{\times }})=\mathbf{W}_{2,1^{\prime }}$
,
$\unicode[STIX]{x1D70B}_{f}^{-1}(\mathbf{W}_{k^{\times }})=\mathbf{W}_{2,1^{\prime }}$
,
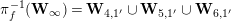 $\unicode[STIX]{x1D70B}_{f}^{-1}(\mathbf{W}_{\infty })=\mathbf{W}_{4,1^{\prime }}\cup \mathbf{W}_{5,1^{\prime }}\cup \mathbf{W}_{6,1^{\prime }}$
and
$\unicode[STIX]{x1D70B}_{f}^{-1}(\mathbf{W}_{\infty })=\mathbf{W}_{4,1^{\prime }}\cup \mathbf{W}_{5,1^{\prime }}\cup \mathbf{W}_{6,1^{\prime }}$
and
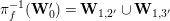 $\unicode[STIX]{x1D70B}_{f}^{-1}(\mathbf{W}_{0}^{\prime })=\mathbf{W}_{1,2^{\prime }}\cup \mathbf{W}_{1,3^{\prime }}$
. Hence, we have the claim by Proposition 3.1 and [Reference ColemanCo, Lemma 1.4].◻
$\unicode[STIX]{x1D70B}_{f}^{-1}(\mathbf{W}_{0}^{\prime })=\mathbf{W}_{1,2^{\prime }}\cup \mathbf{W}_{1,3^{\prime }}$
. Hence, we have the claim by Proposition 3.1 and [Reference ColemanCo, Lemma 1.4].◻
The smooth projective curves
![]() $\overline{\mathbf{Y}}_{1,2}^{\text{c}}$
and
$\overline{\mathbf{Y}}_{1,2}^{\text{c}}$
and
![]() $\overline{\mathbf{Y}}_{2,1}^{\text{c}}$
have defining equations
$\overline{\mathbf{Y}}_{2,1}^{\text{c}}$
have defining equations
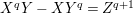 $X^{q}Y-XY^{q}=Z^{q+1}$
determined by the equation in Propositions 4.2 and 4.3. The infinity points of
$X^{q}Y-XY^{q}=Z^{q+1}$
determined by the equation in Propositions 4.2 and 4.3. The infinity points of
![]() $\overline{\mathbf{Y}}_{1,2}$
in
$\overline{\mathbf{Y}}_{1,2}$
in
![]() $\mathbb{P}_{k}^{2}$
consist of
$\mathbb{P}_{k}^{2}$
consist of
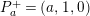 $P_{a}^{+}=(a,1,0)$
for
$P_{a}^{+}=(a,1,0)$
for
![]() $a\in k$
and
$a\in k$
and
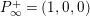 $P_{\infty }^{+}=(1,0,0)$
. The infinity points of
$P_{\infty }^{+}=(1,0,0)$
. The infinity points of
![]() $\overline{\mathbf{Y}}_{2,1}$
consist of
$\overline{\mathbf{Y}}_{2,1}$
consist of
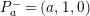 $P_{a}^{-}=(a,1,0)$
for
$P_{a}^{-}=(a,1,0)$
for
![]() $a\in k$
and
$a\in k$
and
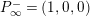 $P_{\infty }^{-}=(1,0,0)$
.
$P_{\infty }^{-}=(1,0,0)$
.
For a wide open space
![]() $W$
, let
$W$
, let
![]() $e(W)$
be the number of ends of
$e(W)$
be the number of ends of
![]() $W$
, and let
$W$
, and let
![]() $g(W)$
be the genus of
$g(W)$
be the genus of
![]() $W$
(cf. [Reference Coleman and McMurdyCM, p. 369 and p. 380]). For a proper smooth curve
$W$
(cf. [Reference Coleman and McMurdyCM, p. 369 and p. 380]). For a proper smooth curve
![]() $C$
over
$C$
over
![]() $k^{\text{ac}}$
, we write
$k^{\text{ac}}$
, we write
![]() $g(C)$
for the genus of
$g(C)$
for the genus of
![]() $C$
.
$C$
.
Theorem 7.14. The covering
![]() ${\mathcal{C}}_{1}(\mathfrak{p}^{3})$
is a semistable covering of
${\mathcal{C}}_{1}(\mathfrak{p}^{3})$
is a semistable covering of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
over some finite extension.
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
over some finite extension.
Proof. We consider the stable covering of
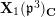 $\mathbf{X}_{1}(\mathfrak{p}^{3})_{\mathbf{C}}$
by Proposition 4.11. Then,
$\mathbf{X}_{1}(\mathfrak{p}^{3})_{\mathbf{C}}$
by Proposition 4.11. Then,
![]() $\overline{\mathbf{Y}}_{1,2}^{\text{c}}$
and
$\overline{\mathbf{Y}}_{1,2}^{\text{c}}$
and
![]() $\overline{\mathbf{Y}}_{2,1}^{\text{c}}$
appear in the stable reduction of
$\overline{\mathbf{Y}}_{2,1}^{\text{c}}$
appear in the stable reduction of
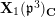 $\mathbf{X}_{1}(\mathfrak{p}^{3})_{\mathbf{C}}$
as irreducible components by Proposition 7.11. The point
$\mathbf{X}_{1}(\mathfrak{p}^{3})_{\mathbf{C}}$
as irreducible components by Proposition 7.11. The point
![]() $P_{0}^{+}$
is the unique infinity point of
$P_{0}^{+}$
is the unique infinity point of
![]() $\overline{\mathbf{Y}}_{1,2}$
whose tube is contained in
$\overline{\mathbf{Y}}_{1,2}$
whose tube is contained in
![]() $\mathbf{W}_{1,1^{\prime }}^{+}$
, because
$\mathbf{W}_{1,1^{\prime }}^{+}$
, because
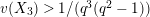 $v(X_{3})>1/(q^{3}(q^{2}-1))$
in
$v(X_{3})>1/(q^{3}(q^{2}-1))$
in
![]() $\mathbf{W}_{1,1^{\prime }}^{+}$
. Similarly,
$\mathbf{W}_{1,1^{\prime }}^{+}$
. Similarly,
![]() $P_{0}^{-}$
is the unique infinity point of
$P_{0}^{-}$
is the unique infinity point of
![]() $\overline{\mathbf{Y}}_{2,1}$
whose tube is contained in
$\overline{\mathbf{Y}}_{2,1}$
whose tube is contained in
![]() $\mathbf{W}_{1,1^{\prime }}^{-}$
. Hence, we have
$\mathbf{W}_{1,1^{\prime }}^{-}$
. Hence, we have
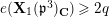 $e(\mathbf{X}_{1}(\mathfrak{p}^{3})_{\mathbf{C}})\geqslant 2q$
by Lemma 7.13. Therefore, we have
$e(\mathbf{X}_{1}(\mathfrak{p}^{3})_{\mathbf{C}})\geqslant 2q$
by Lemma 7.13. Therefore, we have
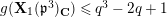 $g(\mathbf{X}_{1}(\mathfrak{p}^{3})_{\mathbf{C}})\leqslant q^{3}-2q+1$
by Lemma 7.10. On the other hand, we have
$g(\mathbf{X}_{1}(\mathfrak{p}^{3})_{\mathbf{C}})\leqslant q^{3}-2q+1$
by Lemma 7.10. On the other hand, we have
 $$\begin{eqnarray}g(\mathbf{X}_{1}(\mathfrak{p}^{3})_{\boldsymbol{ C}})\geqslant g(\overline{\mathbf{Y}}_{1,2}^{\text{c}})+g(\overline{\mathbf{Y}}_{2,1}^{\text{c}})+\left\{\begin{array}{@{}ll@{}}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})}g(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}})\quad & \text{if }q\text{ is odd},\\ \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D701}\in k_{2}^{\times },\,\unicode[STIX]{x1D701}^{\prime }\in k^{\times }}g(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}^{\text{c}})\quad & \text{if }q\text{ is even},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}g(\mathbf{X}_{1}(\mathfrak{p}^{3})_{\boldsymbol{ C}})\geqslant g(\overline{\mathbf{Y}}_{1,2}^{\text{c}})+g(\overline{\mathbf{Y}}_{2,1}^{\text{c}})+\left\{\begin{array}{@{}ll@{}}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})}g(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701}}^{\text{c}})\quad & \text{if }q\text{ is odd},\\ \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D701}\in k_{2}^{\times },\,\unicode[STIX]{x1D701}^{\prime }\in k^{\times }}g(\overline{\mathbf{X}}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}^{\text{c}})\quad & \text{if }q\text{ is even},\end{array}\right.\end{eqnarray}$$
where the summation on the right-hand side is
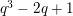 $q^{3}-2q+1$
by Propositions 7.3, 7.6 and 7.9. Then, the affinoids
$q^{3}-2q+1$
by Propositions 7.3, 7.6 and 7.9. Then, the affinoids
![]() $\mathbf{Y}_{1,2}$
,
$\mathbf{Y}_{1,2}$
,
![]() $\mathbf{Y}_{2,1}$
,
$\mathbf{Y}_{2,1}$
,
![]() $\mathbf{X}_{\unicode[STIX]{x1D701}}$
for
$\mathbf{X}_{\unicode[STIX]{x1D701}}$
for
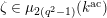 $\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})$
and
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{2(q^{2}-1)}(k^{\text{ac}})$
and
![]() $\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
for
$\mathbf{X}_{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }}$
for
![]() $\unicode[STIX]{x1D701}\in k_{2}^{\times }$
and
$\unicode[STIX]{x1D701}\in k_{2}^{\times }$
and
![]() $\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
are underlying affinoids of basic wide open spaces in the stable covering by Proposition 7.11 and Lemma 7.13. Therefore, by the above genus inequalities, we see that
$\unicode[STIX]{x1D701}^{\prime }\in k^{\times }$
are underlying affinoids of basic wide open spaces in the stable covering by Proposition 7.11 and Lemma 7.13. Therefore, by the above genus inequalities, we see that
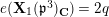 $e(\mathbf{X}_{1}(\mathfrak{p}^{3})_{\mathbf{C}})=2q$
, and the connected components of
$e(\mathbf{X}_{1}(\mathfrak{p}^{3})_{\mathbf{C}})=2q$
, and the connected components of
![]() $\mathbf{W}_{1,2^{\prime }}$
,
$\mathbf{W}_{1,2^{\prime }}$
,
![]() $\mathbf{W}_{1,3^{\prime }}$
,
$\mathbf{W}_{1,3^{\prime }}$
,
![]() $\mathbf{W}_{2,1^{\prime }}$
and
$\mathbf{W}_{2,1^{\prime }}$
and
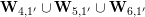 $\mathbf{W}_{4,1^{\prime }}\cup \mathbf{W}_{5,1^{\prime }}\cup \mathbf{W}_{6,1^{\prime }}$
are open annuli.
$\mathbf{W}_{4,1^{\prime }}\cup \mathbf{W}_{5,1^{\prime }}\cup \mathbf{W}_{6,1^{\prime }}$
are open annuli.
The connected components of
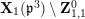 $\mathbf{X}_{1}(\mathfrak{p}^{3})\setminus \mathbf{Z}_{1,1}^{0}$
are two wide open spaces, because each connected component is connected to
$\mathbf{X}_{1}(\mathfrak{p}^{3})\setminus \mathbf{Z}_{1,1}^{0}$
are two wide open spaces, because each connected component is connected to
![]() $\mathbf{Z}_{1,1}^{0}$
at an open subannulus by Lemma 7.12. Then, we see that these two wide open spaces are basic wide open spaces with underlying affinoids
$\mathbf{Z}_{1,1}^{0}$
at an open subannulus by Lemma 7.12. Then, we see that these two wide open spaces are basic wide open spaces with underlying affinoids
![]() $\mathbf{Y}_{1,2}$
and
$\mathbf{Y}_{1,2}$
and
![]() $\mathbf{Y}_{2,1}$
by the above genus inequalities. Therefore, we have the claim by Propositions 4.7, 4.9 and 4.10.◻
$\mathbf{Y}_{2,1}$
by the above genus inequalities. Therefore, we have the claim by Propositions 4.7, 4.9 and 4.10.◻
7.3 Structure of cohomology
In this subsection, we study the action of
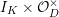 $I_{K}\times {\mathcal{O}}_{D}^{\times }$
on
$I_{K}\times {\mathcal{O}}_{D}^{\times }$
on
![]() $\ell$
-adic cohomology of
$\ell$
-adic cohomology of
![]() $\mathbf{X}_{1}(\mathfrak{p}^{3})$
. We put
$\mathbf{X}_{1}(\mathfrak{p}^{3})$
. We put
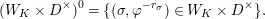 $$\begin{eqnarray}(W_{K}\times D^{\times })^{0}=\{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D711}^{-r_{\unicode[STIX]{x1D70E}}})\in W_{K}\times D^{\times }\}.\end{eqnarray}$$
$$\begin{eqnarray}(W_{K}\times D^{\times })^{0}=\{(\unicode[STIX]{x1D70E},\unicode[STIX]{x1D711}^{-r_{\unicode[STIX]{x1D70E}}})\in W_{K}\times D^{\times }\}.\end{eqnarray}$$
Although it is possible to study the action of
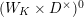 $(W_{K}\times D^{\times })^{0}$
using the result of Section 6, here we study only the inertia action for simplicity. The result in this subsection is essentially used in [Reference Imai and TsushimaIT3].
$(W_{K}\times D^{\times })^{0}$
using the result of Section 6, here we study only the inertia action for simplicity. The result in this subsection is essentially used in [Reference Imai and TsushimaIT3].
Let
![]() ${\mathcal{X}}_{1}(\mathfrak{p}^{3})$
be the semistable formal scheme constructed from
${\mathcal{X}}_{1}(\mathfrak{p}^{3})$
be the semistable formal scheme constructed from
![]() ${\mathcal{C}}_{1}(\mathfrak{p}^{3})$
by [Reference Imai and TsushimaIT2, Theorem 3.5]. The semistable reduction of
${\mathcal{C}}_{1}(\mathfrak{p}^{3})$
by [Reference Imai and TsushimaIT2, Theorem 3.5]. The semistable reduction of
![]() ${\mathcal{X}}_{1}(\mathfrak{p}^{3})$
means the underlying reduced scheme of
${\mathcal{X}}_{1}(\mathfrak{p}^{3})$
means the underlying reduced scheme of
![]() ${\mathcal{X}}_{1}(\mathfrak{p}^{3})$
, which is denoted by
${\mathcal{X}}_{1}(\mathfrak{p}^{3})$
, which is denoted by
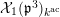 ${\mathcal{X}}_{1}(\mathfrak{p}^{3})_{k^{\text{ac}}}$
.
${\mathcal{X}}_{1}(\mathfrak{p}^{3})_{k^{\text{ac}}}$
.
Lemma 7.15. The smooth projective curves
![]() $\overline{\mathbf{Y}}_{1,2}^{\text{c}}$
and
$\overline{\mathbf{Y}}_{1,2}^{\text{c}}$
and
![]() $\overline{\mathbf{Y}}_{2,1}^{\text{c}}$
intersect with
$\overline{\mathbf{Y}}_{2,1}^{\text{c}}$
intersect with
![]() $\overline{\mathbf{Z}}_{1,1}^{\text{c}}$
at
$\overline{\mathbf{Z}}_{1,1}^{\text{c}}$
at
![]() $P_{0}^{+}$
and
$P_{0}^{+}$
and
![]() $P_{0}^{-}$
respectively in the stable reduction
$P_{0}^{-}$
respectively in the stable reduction
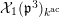 ${\mathcal{X}}_{1}(\mathfrak{p}^{3})_{k^{\text{ac}}}$
.
${\mathcal{X}}_{1}(\mathfrak{p}^{3})_{k^{\text{ac}}}$
.
Proof. We see this from the proof of Theorem 7.14. ◻
Let
![]() $\unicode[STIX]{x1D6E4}$
be the graph defined by the following.
$\unicode[STIX]{x1D6E4}$
be the graph defined by the following.
-
∙ The set of the vertexes of
 $\unicode[STIX]{x1D6E4}$
consists of
$\unicode[STIX]{x1D6E4}$
consists of
 $P_{0}$
,
$P_{0}$
,
 $P_{\infty }$
,
$P_{\infty }$
,
 $P_{a}^{+}$
and
$P_{a}^{+}$
and
 $P_{a}^{-}$
for
$P_{a}^{-}$
for
 $a\in \mathbb{P}^{1}(k)\setminus \{0\}$
.
$a\in \mathbb{P}^{1}(k)\setminus \{0\}$
. -
∙ The set of the edges of
 $\unicode[STIX]{x1D6E4}$
consists of
$\unicode[STIX]{x1D6E4}$
consists of
 $P_{0}P_{a}^{+}$
,
$P_{0}P_{a}^{+}$
,
 $P_{0}P_{a}^{-}$
,
$P_{0}P_{a}^{-}$
,
 $P_{\infty }P_{a}^{+}$
and
$P_{\infty }P_{a}^{+}$
and
 $P_{\infty }P_{a}^{-}$
for
$P_{\infty }P_{a}^{-}$
for
 $a\in \mathbb{P}^{1}(k)\setminus \{0\}$
.
$a\in \mathbb{P}^{1}(k)\setminus \{0\}$
.
We note that
![]() $P_{a}^{+}$
and
$P_{a}^{+}$
and
![]() $P_{a}^{-}$
for
$P_{a}^{-}$
for
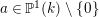 $a\in \mathbb{P}^{1}(k)\setminus \{0\}$
are points of
$a\in \mathbb{P}^{1}(k)\setminus \{0\}$
are points of
![]() $\overline{\mathbf{Y}}_{1,2}^{\text{c}}$
and
$\overline{\mathbf{Y}}_{1,2}^{\text{c}}$
and
![]() $\overline{\mathbf{Y}}_{2,1}^{\text{c}}$
that are not on
$\overline{\mathbf{Y}}_{2,1}^{\text{c}}$
that are not on
![]() $\overline{\mathbf{Z}}_{1,1}^{\text{c}}$
by Lemma 7.15. Let
$\overline{\mathbf{Z}}_{1,1}^{\text{c}}$
by Lemma 7.15. Let
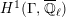 $H^{1}(\unicode[STIX]{x1D6E4},\overline{\mathbb{Q}}_{\ell })$
be the cohomology group of
$H^{1}(\unicode[STIX]{x1D6E4},\overline{\mathbb{Q}}_{\ell })$
be the cohomology group of
![]() $\unicode[STIX]{x1D6E4}$
with coefficients in
$\unicode[STIX]{x1D6E4}$
with coefficients in
![]() $\overline{\mathbb{Q}}_{\ell }$
(cf. [Reference Imai and TsushimaIT2, Section 2]). The group
$\overline{\mathbb{Q}}_{\ell }$
(cf. [Reference Imai and TsushimaIT2, Section 2]). The group
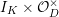 $I_{K}\times {\mathcal{O}}_{D}^{\times }$
acts on
$I_{K}\times {\mathcal{O}}_{D}^{\times }$
acts on
![]() $P_{a}^{+}$
and
$P_{a}^{+}$
and
![]() $P_{a}^{-}$
for
$P_{a}^{-}$
for
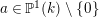 $a\in \mathbb{P}^{1}(k)\setminus \{0\}$
via the action on
$a\in \mathbb{P}^{1}(k)\setminus \{0\}$
via the action on
![]() $\overline{\mathbf{Y}}_{1,2}^{\text{c}}$
and
$\overline{\mathbf{Y}}_{1,2}^{\text{c}}$
and
![]() $\overline{\mathbf{Y}}_{2,1}^{\text{c}}$
. Let
$\overline{\mathbf{Y}}_{2,1}^{\text{c}}$
. Let
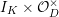 $I_{K}\times {\mathcal{O}}_{D}^{\times }$
act on
$I_{K}\times {\mathcal{O}}_{D}^{\times }$
act on
![]() $P_{0}$
and
$P_{0}$
and
![]() $P_{\infty }$
trivially. By this action, we consider
$P_{\infty }$
trivially. By this action, we consider
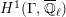 $H^{1}(\unicode[STIX]{x1D6E4},\overline{\mathbb{Q}}_{\ell })$
as a
$H^{1}(\unicode[STIX]{x1D6E4},\overline{\mathbb{Q}}_{\ell })$
as a
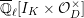 $\overline{\mathbb{Q}}_{\ell }[I_{K}\times {\mathcal{O}}_{D}^{\times }]$
-module.
$\overline{\mathbb{Q}}_{\ell }[I_{K}\times {\mathcal{O}}_{D}^{\times }]$
-module.
Theorem 7.16. We have an exact sequence
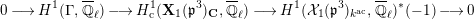 $$\begin{eqnarray}0\longrightarrow H^{1}(\unicode[STIX]{x1D6E4},\overline{\mathbb{Q}}_{\ell })\longrightarrow H_{\text{c}}^{1}(\mathbf{X}_{1}(\mathfrak{p}^{3})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell })\longrightarrow H^{1}({\mathcal{X}}_{1}(\mathfrak{p}^{3})_{k^{\text{ac}}},\overline{\mathbb{Q}}_{\ell })^{\ast }(-1)\longrightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow H^{1}(\unicode[STIX]{x1D6E4},\overline{\mathbb{Q}}_{\ell })\longrightarrow H_{\text{c}}^{1}(\mathbf{X}_{1}(\mathfrak{p}^{3})_{\boldsymbol{ C}},\overline{\mathbb{Q}}_{\ell })\longrightarrow H^{1}({\mathcal{X}}_{1}(\mathfrak{p}^{3})_{k^{\text{ac}}},\overline{\mathbb{Q}}_{\ell })^{\ast }(-1)\longrightarrow 0\end{eqnarray}$$
as representations of
 $(W_{K}\times D^{\times })^{0}$
. Further, as
$(W_{K}\times D^{\times })^{0}$
. Further, as
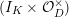 $(I_{K}\times {\mathcal{O}}_{D}^{\times })$
-representations,
$(I_{K}\times {\mathcal{O}}_{D}^{\times })$
-representations,
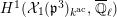 $H^{1}({\mathcal{X}}_{1}(\mathfrak{p}^{3})_{k^{\text{ac}}},\overline{\mathbb{Q}}_{\ell })$
is isomorphic to
$H^{1}({\mathcal{X}}_{1}(\mathfrak{p}^{3})_{k^{\text{ac}}},\overline{\mathbb{Q}}_{\ell })$
is isomorphic to
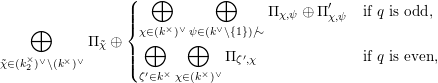 $$\begin{eqnarray}\displaystyle \bigoplus _{\tilde{\unicode[STIX]{x1D712}}\in (k_{2}^{\times })^{\vee }\backslash (k^{\times })^{\vee }}\unicode[STIX]{x1D6F1}_{\tilde{\unicode[STIX]{x1D712}}}\oplus \left\{\begin{array}{@{}ll@{}}\displaystyle \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\bigoplus _{\unicode[STIX]{x1D713}\in (k^{\vee }\backslash \{1\})/\!\sim }\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}\oplus \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }\quad & \text{if }q\text{ is odd},\\ \displaystyle \bigoplus _{\unicode[STIX]{x1D701}^{\prime }\in k^{\times }}\bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}}\quad & \text{if }q\text{ is even},\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \bigoplus _{\tilde{\unicode[STIX]{x1D712}}\in (k_{2}^{\times })^{\vee }\backslash (k^{\times })^{\vee }}\unicode[STIX]{x1D6F1}_{\tilde{\unicode[STIX]{x1D712}}}\oplus \left\{\begin{array}{@{}ll@{}}\displaystyle \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\bigoplus _{\unicode[STIX]{x1D713}\in (k^{\vee }\backslash \{1\})/\!\sim }\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}\oplus \unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D712},\unicode[STIX]{x1D713}}^{\prime }\quad & \text{if }q\text{ is odd},\\ \displaystyle \bigoplus _{\unicode[STIX]{x1D701}^{\prime }\in k^{\times }}\bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D712}}\quad & \text{if }q\text{ is even},\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$
where we put
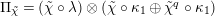 $\unicode[STIX]{x1D6F1}_{\tilde{\unicode[STIX]{x1D712}}}=(\tilde{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D706})\otimes (\tilde{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D705}_{1}\oplus \tilde{\unicode[STIX]{x1D712}}^{q}\circ \unicode[STIX]{x1D705}_{1})$
, and
$\unicode[STIX]{x1D6F1}_{\tilde{\unicode[STIX]{x1D712}}}=(\tilde{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D706})\otimes (\tilde{\unicode[STIX]{x1D712}}\circ \unicode[STIX]{x1D705}_{1}\oplus \tilde{\unicode[STIX]{x1D712}}^{q}\circ \unicode[STIX]{x1D705}_{1})$
, and
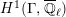 $H^{1}(\unicode[STIX]{x1D6E4},\overline{\mathbb{Q}}_{\ell })$
is isomorphic to
$H^{1}(\unicode[STIX]{x1D6E4},\overline{\mathbb{Q}}_{\ell })$
is isomorphic to
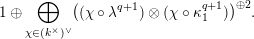 $$\begin{eqnarray}1\oplus \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}((\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D706}^{q+1})\otimes (\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D705}_{1}^{q+1}))^{\oplus 2}.\end{eqnarray}$$
$$\begin{eqnarray}1\oplus \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}((\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D706}^{q+1})\otimes (\unicode[STIX]{x1D712}\circ \unicode[STIX]{x1D705}_{1}^{q+1}))^{\oplus 2}.\end{eqnarray}$$
Proof. The existence of the exact sequence follows from [Reference Imai and TsushimaIT2, Theorem 5.3] and Lemma 7.15 using Poincaré duality (cf. [Reference FarguesFar1, Proposition 5.9.2]). We know the structure of
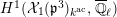 $H^{1}({\mathcal{X}}_{1}(\mathfrak{p}^{3})_{k^{\text{ac}}},\overline{\mathbb{Q}}_{\ell })$
by Propositions 7.3, 7.6 and 7.9.
$H^{1}({\mathcal{X}}_{1}(\mathfrak{p}^{3})_{k^{\text{ac}}},\overline{\mathbb{Q}}_{\ell })$
by Propositions 7.3, 7.6 and 7.9.
We study the structure of
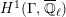 $H^{1}(\unicode[STIX]{x1D6E4},\overline{\mathbb{Q}}_{\ell })$
. By Lemma 5.1 and Lemma 6.2, the action of
$H^{1}(\unicode[STIX]{x1D6E4},\overline{\mathbb{Q}}_{\ell })$
. By Lemma 5.1 and Lemma 6.2, the action of
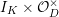 $I_{K}\times {\mathcal{O}}_{D}^{\times }$
on
$I_{K}\times {\mathcal{O}}_{D}^{\times }$
on
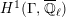 $H^{1}(\unicode[STIX]{x1D6E4},\overline{\mathbb{Q}}_{\ell })$
factors through
$H^{1}(\unicode[STIX]{x1D6E4},\overline{\mathbb{Q}}_{\ell })$
factors through
![]() $k^{\times }$
. We can check that
$k^{\times }$
. We can check that
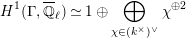 $$\begin{eqnarray}H^{1}(\unicode[STIX]{x1D6E4},\overline{\mathbb{Q}}_{\ell })\simeq 1\oplus \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\unicode[STIX]{x1D712}^{\oplus 2}\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(\unicode[STIX]{x1D6E4},\overline{\mathbb{Q}}_{\ell })\simeq 1\oplus \bigoplus _{\unicode[STIX]{x1D712}\in (k^{\times })^{\vee }}\unicode[STIX]{x1D712}^{\oplus 2}\end{eqnarray}$$
as representations of
![]() $k^{\times }$
. Hence, the claim follows from Lemmas 5.1 and 6.2.◻
$k^{\times }$
. Hence, the claim follows from Lemmas 5.1 and 6.2.◻
Acknowledgments
The authors thank Seidai Yasuda for helpful discussion on the subject in Section 6.2.2. They are grateful to a referee for suggestions for improvements.