Research Article
On a Formalism Which Makes any Sequence of Symbols Well-Formed
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-4
-
- Article
-
- You have access
- Export citation
A Note on Triple Systems and Totally Geodesic Submanifolds in a Homogeneous Space
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 5-20
-
- Article
-
- You have access
- Export citation
Higher Derivations and Central Simple Algebras
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 21-30
-
- Article
-
- You have access
- Export citation
ε-Entropy of the Brownian Motion with the Multi-Dimensional Spherical Parameter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 31-40
-
- Article
-
- You have access
- Export citation
II-Principal Hereditary Orders
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 41-65
-
- Article
-
- You have access
- Export citation
Prolongations of G-Structures to Tangent Bundles
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 67-108
-
- Article
-
- You have access
- Export citation
Homotopy Groups of Compact Lie Groups E6, E7 and E8
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 109-139
-
- Article
-
- You have access
- Export citation
Spectral Type of One-Parameter Group of Unitary Operators with Transversal Group
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 141-153
-
- Article
-
- You have access
- Export citation
On Signed Branching Markov Processes with Age
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 155-225
-
- Article
-
- You have access
- Export citation
Automorphism Groups of Jordan Algebras
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 227-235
-
- Article
-
- You have access
- Export citation
Existence of Non-Trivial Deformations of Inseparable Algebraic Extension Fields II*
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 237-245
-
- Article
-
- You have access
- Export citation
On the Galois Cohomology Group of the Ring of Integers in a Global Field and its Adele Ring
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 247-252
-
- Article
-
- You have access
- Export citation
Semi-Primary QF-3 Rings
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 253-258
-
- Article
-
- You have access
- Export citation
Über Diskontinuierliche Gruppen Picardschen Typus und Zugehörige Eisensteinsche Reihen
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 259-271
-
- Article
-
- You have access
- Export citation
Note on Schiffer’s Variation in the Class of Univalent Functions in the Unit Disc
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 273-276
-
- Article
-
- You have access
- Export citation
A Criterion for Normalcy
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 277-282
-
- Article
-
- You have access
- Export citation
On Groups All of whose 2-Blocks Have the Highest Defects
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 283-286
-
- Article
-
- You have access
- Export citation
A Remark on the Continuity of the Dual Process
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 287-295
-
- Article
-
- You have access
- Export citation
Approximation of Uniform Transport Process on a Finite Interval to Brownian Motion
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 297-314
-
- Article
-
- You have access
- Export citation
Upper Bounds on Homological Dimensions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 315-322
-
- Article
-
- You have access
- Export citation

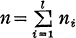 is the dimension of
is the dimension of