Let U0 = [(0, 1); and U1 = (0,1)]. Suppose we have a distribution 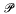 of N points in
of N points in 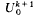 , where, for k ≥ 1,
, where, for k ≥ 1, 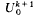 is the unit cube consisting of the points y = (y1, … , yk+1) with 0 ≤ yi < 1 (i = 1 , … , k + 1). For X = (x1 ,…, xk + 1) in
is the unit cube consisting of the points y = (y1, … , yk+1) with 0 ≤ yi < 1 (i = 1 , … , k + 1). For X = (x1 ,…, xk + 1) in 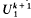 , let B(x) denote the box consisting of all y such that 0 ≤ yi < xi (i = 1 ,…, k + 1), and let
, let B(x) denote the box consisting of all y such that 0 ≤ yi < xi (i = 1 ,…, k + 1), and let 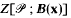 denote the number of points of
denote the number of points of 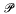 which lie in B(x).
which lie in B(x).