Article contents
Borel isomorphisms at the first level: Corrigenda et addenda
Published online by Cambridge University Press: 26 February 2010
Extract
In recent work [2] we have investigated Borel isomorphisms at the first level, i.e. mappings that together with their inverses map Fσ-sets to Fσ-sets. We are grateful to Dr. F. Topsøe for writing to point out errors in the proofs of our Theorems 2.1, 2.2 and 2.3. The errors escaped our attention because we only wrote out the first step of a complicated inductive argument and carelessly and falsely claimed that the general step of the induction was similar to the first. To be more specific, in the proof of Theorem 2.1, although we do have
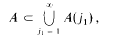
we do not, in general, have
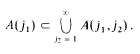
Fortunately the proofs can be corrected.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1980
References
- 2
- Cited by


