Let F: 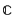 n ×
n × 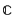 r →
r → 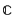 be a sufficiently small representative, defined near (0,0), of a versal unfolding of a germ F0: (
be a sufficiently small representative, defined near (0,0), of a versal unfolding of a germ F0: (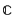 n, 0) → (
n, 0) → (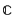 , 0) with isolated singularity at 0∈
, 0) with isolated singularity at 0∈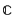 n. Then a result of Teissier ((4), p. 338) says that, for u∈
n. Then a result of Teissier ((4), p. 338) says that, for u∈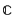 r sufficiently close to 0, F acts as a versal unfolding of all the various singularities, close to 0, on the fibre Fu = 0 (where Fu(x) = F(x, u)). Let us fix a small neighbourhood W of 0 in
r sufficiently close to 0, F acts as a versal unfolding of all the various singularities, close to 0, on the fibre Fu = 0 (where Fu(x) = F(x, u)). Let us fix a small neighbourhood W of 0 in 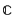 n and restrict u to be so close to 0 that all singularities of Fu lie in W. Suppose that the fibre Fu = 0 has singularities of (contact) type χ1, …, χm, all isolated. Suppose that, for each i, the collection {χij}(1 ≤ j ≤ k(i)) of singularities specializes to χi, that is it occurs on a single fibre arbitrarily close to χi in a versal unfolding of χi. Then Teissier's result shows that there will exist fibres Fv = 0 of F, with v arbitrarily close to u, such that the fibre Fv = 0 carries singularities, all in W, of all the types χij for 1 ≤ i ≤ m, 1 ≤ j ≤ k(i). In other words, if ‘despecializations’ {χij} of the separate singularities χi are possible, then they can all occur together on a single fibre of F, provided F is versal.
n and restrict u to be so close to 0 that all singularities of Fu lie in W. Suppose that the fibre Fu = 0 has singularities of (contact) type χ1, …, χm, all isolated. Suppose that, for each i, the collection {χij}(1 ≤ j ≤ k(i)) of singularities specializes to χi, that is it occurs on a single fibre arbitrarily close to χi in a versal unfolding of χi. Then Teissier's result shows that there will exist fibres Fv = 0 of F, with v arbitrarily close to u, such that the fibre Fv = 0 carries singularities, all in W, of all the types χij for 1 ≤ i ≤ m, 1 ≤ j ≤ k(i). In other words, if ‘despecializations’ {χij} of the separate singularities χi are possible, then they can all occur together on a single fibre of F, provided F is versal.