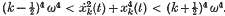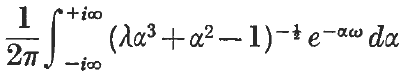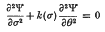Research Article
Some enumerative formulae for algebraic curves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 399-416
-
- Article
- Export citation
On the stabilization of matrices and the convergence of linear iterative processes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 417-425
-
- Article
- Export citation
A differential equation for undamped forced non-linear oscillations. II†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 426-438
-
- Article
- Export citation
The statistical distribution of the curvature of a random Gaussian surface
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 439-453
-
- Article
- Export citation
Numerical evaluation of the integral
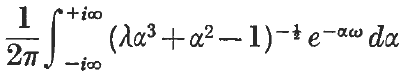
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 454-462
-
- Article
- Export citation
The effect of selection in a haploid genetic population
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 463-467
-
- Article
- Export citation
The distribution of gene frequency in a bisexual diploid population
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 468-474
-
- Article
- Export citation
Recurrence relations for oscillator-well radial integrals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 475-478
-
- Article
- Export citation
Diffraction by a wide slit and complementary strip. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 479-496
-
- Article
- Export citation
Diffraction by a wide slit and complementary strip. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 497-511
-
- Article
- Export citation
Variational principles in high-frequency scattering*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 512-529
-
- Article
- Export citation
Scattering of plane waves by locally homogeneous dielectric noise†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 530-537
-
- Article
- Export citation
The solution of boundary value problems for a general hodograph equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 538-553
-
- Article
- Export citation
Research Notes
On A4 + B4 + C4 + D4 = E4
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 554-555
-
- Article
- Export citation
Embeddings of real projective spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 555-557
-
- Article
- Export citation
A note concerning invariant subspaces of a bounded linear operator on a Banach space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 557-559
-
- Article
- Export citation
Discontinuous linear functionals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 559-560
-
- Article
- Export citation
A note on the relation between scattering phase and bound states
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 560-561
-
- Article
- Export citation
Proceedings at the meetings
Proceedings of the Meetings held during the session 1957–1958
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 562-565
-
- Article
- Export citation
Statement of Accounts
Cambridge philosophical society Statement of Accounts for the year ended 31 December 1957
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 566-568
-
- Article
- Export citation


 of periodic solutions or, equivalently, that a topological transformation
of periodic solutions or, equivalently, that a topological transformation