Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T14:01:46.814Z Has data issue: false hasContentIssue false
  • English
  • Français

The solution of boundary value problems for a general hodograph equation

Published online by Cambridge University Press:  24 October 2008

A. G. Mackie
A. G. Mackie
Affiliation:
St Salvator's CollegeSt Andrews
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper the solution is found of certain boundary value problems appropriate to the flow of an invisoid, compressible fluid past a wedge-shaped profile. The most general hodograph equation in the form

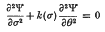
is used. Expressions are found for the position coordinates and the drag. The resulting solutions are then discussed for functions k(σ) appropriate to Chaplygin's equation, Tricomi's equation and the equation of Tomotika and Tamada. The case of Helmholtz flow past a wedge with sonic velocity upstream is treated in detail, and the resulting expressions for the drag enable an estimate to be made of the error which results in using approximations to Chaplygin's equation.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 54 , Issue 4 , October 1958 , pp. 538 - 553
Copyright
Copyright © Cambridge Philosophical Society 1958

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cherry, T. M.Proc. Boy. Soc. A, 202 (1950), 507.Google Scholar
(2)Cole, J. D.J. Math. Phys. 30 (1951), 79.Google Scholar
(3)Germain, P. J.Bat. Mech. Anal. 4 (1955), 925.Google Scholar
(4)Goldstein, S., Lighthill, M. J. and Craggs, J. W.Quart. J. Mech. Appl. Math. 1 (1948), 344.Google Scholar
(5)Helliwell, J. B. and Mackie, A. G.J. Fluid Mech. 3 (1957), 93.Google Scholar
(6)Imai, I.J. Aero. Sci. 19 (1952), 496.CrossRefGoogle Scholar
(7)Lighthill, M. J.Proc. Boy. Soc. A, 191 (1947), 341.Google Scholar
(8)Lighthill, M. J.Proc. Boy. Soc. A, 191 (1947), 352.Google Scholar
(9)Mackie, A. G. and Pack, D. C.Proc. Camb. Phil. Soc. 48 (1952), 178.Google Scholar
(10)Mackie, A. G. and Pack, D. C.J. Rat. Mech. Anal. 4 (1955), 177.Google Scholar
(11)Roshko, A.Nat. Adv. Comm. Aero., Wash., Tech. Note no. 3168 (1954).Google Scholar
(12)Tomotika, S. and Tamada, T.Quart. Appl. Math. 9 (1951), 129.Google Scholar
(13)Weinstein, A.Proc. Naval Ordnance Laboratory Aeroballistic Research Symposia (1950).Google Scholar