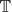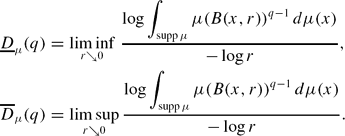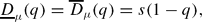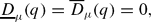Research Article
Cubic surfaces over finite fields
-
- Published online by Cambridge University Press:
- 07 July 2010, pp. 385-388
-
- Article
-
- You have access
- Export citation
On modular signs
-
- Published online by Cambridge University Press:
- 19 July 2010, pp. 389-411
-
- Article
- Export citation
The Brauer–Manin obstruction for integral points on curves
-
- Published online by Cambridge University Press:
- 24 June 2010, pp. 413-421
-
- Article
- Export citation
Exel's crossed product for non-unital C*-algebras
-
- Published online by Cambridge University Press:
- 19 July 2010, pp. 423-444
-
- Article
- Export citation
Catalan loops
-
- Published online by Cambridge University Press:
- 19 July 2010, pp. 445-453
-
- Article
- Export citation
Stable splittings, spaces of representations and almost commuting elements in Lie groups
-
- Published online by Cambridge University Press:
- 03 June 2010, pp. 455-490
-
- Article
- Export citation
Positive-entropy integrable systems and the Toda lattice, II
-
- Published online by Cambridge University Press:
- 19 July 2010, pp. 491-538
-
- Article
- Export citation
Cup-length estimates for leaf-wise intersections
-
- Published online by Cambridge University Press:
- 21 July 2010, pp. 539-551
-
- Article
- Export citation
Prevalent Lq-dimensions of measures
-
- Published online by Cambridge University Press:
- 24 June 2010, pp. 553-571
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 149 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 October 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PSP volume 149 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 05 October 2010, pp. b1-b6
-
- Article
-
- You have access
- Export citation