Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T14:10:25.990Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive-entropy integrable systems and the Toda lattice, II

Published online by Cambridge University Press:  19 July 2010

LEO T. BUTLER
LEO T. BUTLER*
Affiliation:
School of Mathematics, The University of Edinburgh, 6214 James Clerk Maxwell Building, Edinburgh, EH9 3JZ, UK. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper constructs completely integrable convex Hamiltonians on the cotangent bundle of certain 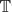k bundles over 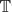l. A central role is played by the Lax representation of a Bogoyavlenskij–Toda lattice. The classification of these systems, up to iso-energetic topological conjugacy, is related to the classification of abelian groups of Anosov toral automorphisms by their topological entropy function.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 149 , Issue 3 , November 2010 , pp. 491 - 538
Copyright
Copyright © Cambridge Philosophical Society 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Adler, M. and van Moerbeke, P.Completely integrable systems, Euclidean Lie algebras, and curves. Adv. Math. 38 (3) (1980), 267–317.CrossRefGoogle Scholar
[2]Adler, M. and van Moerbeke, P.Linearization of Hamiltonian systems, Jacobi varieties and representation theory. Adv. Math. 38 (3) (1980), 318–379.CrossRefGoogle Scholar
[3]Adler, M. and van Moerbeke, P.Kowalewski's asymptotic method, Kac-Moody Lie algebras and regularization. Comm. Math. Phys. 83 (1) (1982), 83–106.CrossRefGoogle Scholar
[4]Bogoyavlenskij, O. I.On perturbations of the periodic Toda lattice. Comm. Math. Phys. 51 (3) (1976), 201–209.CrossRefGoogle Scholar
[5]Bolsinov, A. V. and Ĭovanovich, B.Integrable geodesic flows on homogeneous spaces. Mat. Sb. 192 (7) (2001), 21–40. Translation in Sb. Math. 192(7–8) (2001), 951–968.Google Scholar
[6]Bolsinov, A. V. and Taimanov, I. A.Integrable geodesic flows with positive topological entropy. Invent. Math. 140 (3) (2000), 639–650.Google Scholar
[7]Bolsinov, A. V. and Taimanov, I. A.Integrable geodesic flows on suspensions of automorphisms of tori. (Russian) Tr. Mat. Inst. Steklova 231 (2000), Din. Sist., Avtom. i Beskon. Gruppy, 46–63. Translation in Proc. Steklov Inst. Math. 231(4) (2000), 42–58.Google Scholar
[8]Boyd, D. W.Reciprocal Polynomials having small measure. Math. Comp. 53 (187) (1989), 355–357.CrossRefGoogle Scholar
[9]Bloch, A. and Gekhtman, M.Hamiltonian and gradient structures in the Toda flows. J. Geom. Phys. 27 (3–4) (1998), 230–248.CrossRefGoogle Scholar
[10]Butler, L.Invariant fibrations of geodesic flows. Topology. 44 (4) (2005), 769–789.CrossRefGoogle Scholar
[11]Butler, L.Positive-entropy integrable systems and the Toda lattice. Inv. Math. 158 (3) (2004), 515–549.CrossRefGoogle Scholar
[12]Butler, L.The Maslov cocycle, smooth structures and real-analytic complete integrability. Amer. J. Math. 131 (5) (2009), 1311–1336.CrossRefGoogle Scholar
[13]Dazord, P. and Delzant, T.Le probleme general des variables actions-angles. J. Differential Geom. 26 (2) (1987), 223–251.CrossRefGoogle Scholar
[14]Dinaburg, E. I.A connection between various entropy characterizations of dynamical systems. Izv. Akad. Nauk SSSR Ser. Mat. 35 (1971), 324–366.Google Scholar
[15]Foxman, J. A. and Robbins, J. M.Singularities, Lax degeneracies and Maslov indices of the periodic Toda chain. Nonlinearity 18 (6) (2005), 2795–2813.CrossRefGoogle Scholar
[16]Foxman, J. A. and Robbins, J. M.The Maslov index and nondegenerate singularities of integrable systems. Nonlinearity 18 (6) (2005), 2775–2794.CrossRefGoogle Scholar
[17]Fulton, W. and Harris, J.Representation theory. A first course. Graduate Texts in Math. 129. (Springer-Verlag, 1991).Google Scholar
[18]The GAP group GAP – Groups, Algorithms and Programming, Version 4.4.6; (2005). http://www.gap-system.orgGoogle Scholar
[19]Gelfond, A. O.Transcendental and Algebraic Numbers (Dover, 1960). Trans. Boron, Leo F..Google Scholar
[20]Katok, A., Katok, S. and Schmidt, K.Rigidity of measurable structure for Zd-actions by automorphisms of a torus. Comment. Math. Helv. 77 (4) (2002), 718–745.CrossRefGoogle Scholar
[21]Kostant, B.The solution to a generalized Toda lattice and representation theory. Adv. in Math. 34 (3) (1979), 195–338.CrossRefGoogle Scholar
[22]Kozlov, V. V.Symmetries, topology and resonances in Hamiltonian mechanics. Translated from the Russian manuscript by Bolotin, S. V., Treshchev, D. and Fedorov, Yuri Ergebn. Math. Grenzgeb. (3), 31. (Springer-Verlag, 1996).CrossRefGoogle Scholar
[23]Kozlov, V. V. and Treshchev, D. V.Polynomial integrals of Hamiltonian systems with exponential interaction. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 53 (3) (1989), 537–556. Translation in Math. USSR-Izv. 34(3) (1990), 555–574.Google Scholar
[24]Maxima.sourceforge.net Maxima, A Computer Algebra System. Version 5.18.1 http://maxima.sourceforge.net/Google Scholar
[25]Mossinghoff, M. J.Polynomials with small Mahler measure. Math. Comp. 67 (224) (1998), 1697–1705.CrossRefGoogle Scholar
[26]Raghunathan, M. S.Discrete subgroups of Lie groups. Ergeb. Math. Grenzgeb. Band 68. (Springer-Verlag, 1972).CrossRefGoogle Scholar
[27]Reyman, A. G. and Semenov-Tian-Shansky, A. Group-theoretical methods in the theory of finite-dimensional integrable systems, in Dynamical Systems. VII. Integrable Systems, Nonholonomic Dynamical Systems. Encyclopaedia of Mathematical Sciences, 16. (Springer-Verlag, 1994).Google Scholar
[28]Schwartzman, S.Asymptotic cycles. Ann. of Math. 66 (2) (1957), 270–284.CrossRefGoogle Scholar
[29]Wall, C. T. C.Surgery on compact manifolds. Second edition. Edited and with a foreword by Ranicki, A. A. Math. Sur. Monogr. 69 (Amer. Math. Soc. 1999).CrossRefGoogle Scholar