Research Article
Universal matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 193-198
-
- Article
- Export citation
Quaternionic analysis
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 199-225
-
- Article
- Export citation
Algebraic solutions of partizan games with cycles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 227-246
-
- Article
- Export citation
Augmentation quotients of group rings and symmetric powers
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 247-252
-
- Article
- Export citation
Closure operations for Schunck classes and formations of finite solvable groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 253-259
-
- Article
- Export citation
Augmentation quotients of some nonabelian finite groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 261-270
-
- Article
- Export citation
The covariance algebra of an extended covariant system
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 271-280
-
- Article
- Export citation
Remarks on generalized analytic independence
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 281-289
-
- Article
- Export citation
Boundaries for polydisc algebras in infinite dimensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 291-303
-
- Article
- Export citation
Eberlein compacts and spaces of continuous functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 305-313
-
- Article
- Export citation
Footnote to a paper of Baker and Mines
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 315
-
- Article
- Export citation
On the centres of hereditary JBW-subalgebras of a JBW-algebra
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 317-324
-
- Article
- Export citation
Constants relating a Hermitian operator and its square
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 325-333
-
- Article
- Export citation
A note on homology surgery and the Casson–Gordon invariant
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 335-344
-
- Article
- Export citation
On strong almost convergence
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 345-350
-
- Article
- Export citation
The determination of a function from its projections
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 351-355
-
- Article
- Export citation
Inner function images of radii
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 357-360
-
- Article
- Export citation
Generalized approximate methods for transmission through a barrier governed by a differential equation of order 2n
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 361-377
-
- Article
- Export citation
A continuum model of many-body interactions in a perfect crystal
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 379-385
-
- Article
- Export citation
Front matter
PSP volume 85 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation

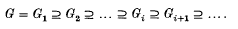
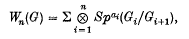
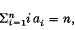 and
and 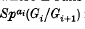 is the
is the 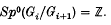
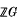 , the group ring of
, the group ring of 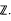 . Define the additive group
. Define the additive group 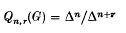
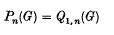
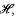 , and let
, and let 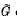 of
of 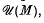 , the unitary group of
, the unitary group of 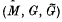 satisfies an additional axiom, we say that it is an extended covariant system. We define a Hilbert space
satisfies an additional axiom, we say that it is an extended covariant system. We define a Hilbert space 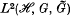 and operators
and operators 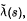 , acting on
, acting on  . The von Neumann algebra
. The von Neumann algebra 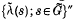 is then the covariance algebra of the extended covariant system
is then the covariance algebra of the extended covariant system 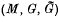 , denoted by
, denoted by 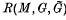 .
.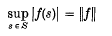

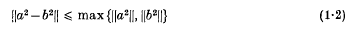


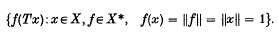
 for diffeomorphisms between the boundaries of manifolds. Here manifolds refer to smooth manifolds.
for diffeomorphisms between the boundaries of manifolds. Here manifolds refer to smooth manifolds.