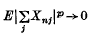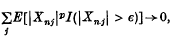Research Article
Applications of outwardly simple line families to plane convex sets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 353-356
-
- Article
- Export citation
On the coefficients of certain automorphic functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 357-367
-
- Article
- Export citation
On the Banach–Saks property
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 369-374
-
- Article
- Export citation
On non-unital Jordan–Banach algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 375-380
-
- Article
- Export citation
The 2-primary J-homomorphism
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 381-387
-
- Article
- Export citation
On stratifying 3-jets of functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 389-400
-
- Article
- Export citation
The ideal structure of the Stone-Čech compactification of a group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 401-409
-
- Article
- Export citation
The left Hilbert algebra associated to a semi-direct product*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 411-418
-
- Article
- Export citation
Non-singular bilinear maps and stable homotopy classes of spheres
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 419-425
-
- Article
- Export citation
An algorithm for the total, or partial, factorization of a polynomial
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 427-437
-
- Article
- Export citation
On the Lp convergence of sums of independent random variables
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 439-446
-
- Article
- Export citation
The asymptotic covariance of two counters
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 447-452
-
- Article
- Export citation
Harmonic balance and the Hopf bifurcation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 453-467
-
- Article
- Export citation
The Hopf bifurcation theorem in three dimensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 469-483
-
- Article
- Export citation
Properties of two-way transmission in generalized wave propagation problems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 485-488
-
- Article
- Export citation
Some remarks on the existence of spacelike hypersurfaces of constant mean curvature
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 489-495
-
- Article
- Export citation
A buckling model for the set of umbilic catastrophes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 497-507
-
- Article
- Export citation
Proceedings of meetings
Proceedings of the meetings held during the session 1976–77
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 509-515
-
- Article
- Export citation
Front matter
PSP volume 82 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 82 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b11
-
- Article
-
- You have access
- Export citation



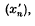 ), which is (
), which is (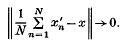
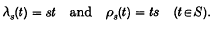

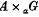 denote the semi-direct product of
denote the semi-direct product of 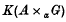 of continuous functions with compact support, has the same achieved left Hilbert algebra,
of continuous functions with compact support, has the same achieved left Hilbert algebra, 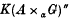 as the crossed product of
as the crossed product of 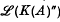 . As a consequence we obtain that the canonical weight on
. As a consequence we obtain that the canonical weight on 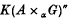 is the dual weight of the canonical weight on
is the dual weight of the canonical weight on 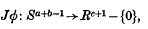
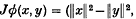 2ø(
2ø(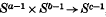 , and then applying the standard Hopf construction ((13), p. 112). In any case, one gets an element [Jø] in
, and then applying the standard Hopf construction ((13), p. 112). In any case, one gets an element [Jø] in 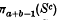 , which in turn determines a stable homotopy class of spheres {Jø} in the
, which in turn determines a stable homotopy class of spheres {Jø} in the  , where
, where  which equals {Jø} for some non-singular bilinear map ø will be called
which equals {Jø} for some non-singular bilinear map ø will be called 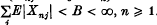 . Let
. Let