Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T13:11:52.746Z Has data issue: false hasContentIssue false
  • English
  • Français

The left Hilbert algebra associated to a semi-direct product*

Published online by Cambridge University Press:  24 October 2008

R. Rousseau
R. Rousseau
Affiliation:
Katholieke Universiteit, Leuven, Belgium
Get access Rights & Permissions [Opens in a new window]

Abstract

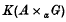Let A and G be locally compact groups and α a continuous action of G on A, and let denote the semi-direct product of A and G. Then we prove that the left Hilbert algebra of continuous functions with compact support, has the same achieved left Hilbert algebra, as the crossed product of K(A)" by the associated action α̃ of G on . As a consequence we obtain that the canonical weight on is the dual weight of the canonical weight on K(A)".

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 82 , Issue 3 , November 1977 , pp. 411 - 418
Copyright
Copyright © Cambridge Philosophical Society 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Digernes, T. Duality for weights on covariant systems and its application (Thesis, U.C.L.A., 1975).Google Scholar
(2)Haagerup, U.On the dual weights for crossed products of von Neumann algebras I (Preprint no. 10, Matematisk Institut Odense, 10 1975).Google Scholar
(3)Loomis, L. H.An introduction to abstract harmonic analysis (Princeton, N.J., D. Van Nostrand Co. Inc, 1953).Google Scholar
(4)Rieffel, M. and Van Daele, A.A bounded operator approach to Tomita-Takesaki theory. Pacific J. Math. 69 (1) (1977).CrossRefGoogle Scholar
(5)Rousseau, R. and Van Daele, A. Crossed products of commutation systems (Preprint K. U. Leuven (1977)).Google Scholar
(6)Stinespring, W. F.Integration theorems for gages and duality for unimodular groups. Trans. Amer. Math. Soc. 90 (1959), 15–56.CrossRefGoogle Scholar
(7)Takesaki, M.Tomita's theory and its applications (Springer Lecture Notes in Math. 128, Heidelberg, 1970).Google Scholar
(8)Takesaki, M.Duality for crossed products and the structure of von Neumann algebras of type III. Acta Math. 131 (1973), 249–310.CrossRefGoogle Scholar
(9)Van Daele, A. Crossed product of von Neumann algebras (Lecture notes K. U. Leuven, 06 1976).Google Scholar