Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Partington, J. R.
1983.
On nearly uniformly convex Banach spaces.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 93,
Issue. 1,
p.
127.
Diestel, Joseph
1984.
Sequences and Series in Banach Spaces.
Vol. 92,
Issue. ,
p.
124.
Castillo, Jesús M. F.
and
Sánchez, Fernando
1993.
Upper lp-estimates in vector sequence spaces, with some applications.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 113,
Issue. 2,
p.
329.
Castillo, Jesús M. F.
and
Simões, Marilda A.
1994.
On the Banach-Saks property in Fréchet spaces.
Results in Mathematics,
Vol. 26,
Issue. 1-2,
p.
18.
Cembranos, Pilar
1994.
The weak Banach-Saks property on Lp(μ, E).
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 115,
Issue. 2,
p.
283.
Hazewinkel, M.
1997.
Encyclopaedia of Mathematics.
p.
71.
Kucher, O. V.
1999.
The grothendieck property in the spacel ∞ (E) and the weak Banach-Saks property inc 0 (E).
Journal of Mathematical Sciences,
Vol. 96,
Issue. 1,
p.
2828.
Cho, Kyugeun
and
Lee, Chongsung
2011.
ALTERNATE SIGNS (Aκ) PROPERTY IN BANACH SPACES.
Korean Journal of Mathematics,
Vol. 19,
Issue. 3,
p.
301.
Cho, Kyugeun
and
Lee, Chongsung
2012.
WEAK PROPERTY (βκ).
Korean Journal of Mathematics,
Vol. 20,
Issue. 4,
p.
415.
Kryczka, Andrzej
2012.
Arithmetic separation and Banach–Saks sets.
Journal of Mathematical Analysis and Applications,
Vol. 394,
Issue. 2,
p.
772.
Kryczka, Andrzej
2013.
Mean separations in Banach spaces under abstract interpolation and extrapolation.
Journal of Mathematical Analysis and Applications,
Vol. 407,
Issue. 2,
p.
281.
Braga, Bruno M.
2014.
On the complexity of some classes of Banach spaces and non-universality.
Czechoslovak Mathematical Journal,
Vol. 64,
Issue. 4,
p.
1123.
Cho, Kyugeun
and
Lee, Chongsung
2015.
SOME UNIFORM GEOMETRICAL PROPERTIES IN BANACH SPACES.
Bulletin of the Korean Mathematical Society,
Vol. 52,
Issue. 2,
p.
505.
Kryczka, Andrzej
and
Kurlej, Konrad
2021.
Regular methods of summability for direct sums of Banach spaces.
Journal of Mathematical Analysis and Applications,
Vol. 494,
Issue. 1,
p.
124636.
Sun, Wenlong
Han, Xiaoying
and
Kloeden, Peter E.
2024.
Approximation of the Heaviside function by sigmoidal functions in reaction–diffusion equations.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 128,
Issue. ,
p.
107656.


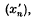 ), which is (
), which is (