Research Article
The densities of the regular polytopes, Part 3*
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-22
-
- Article
- Export citation
The spectrum of the self-adjoint partial differential equation in any domain
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 23-44
-
- Article
- Export citation
Some chains of theorems derived by successive projection
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 45-51
-
- Article
- Export citation
Configurations defined by six lines in space of three dimensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 52-68
-
- Article
- Export citation
The sum of powers as canonical expression
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 69-82
-
- Article
- Export citation
On the prior probability in the theory of sampling
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 83-87
-
- Article
- Export citation
Degenerate surfaces in higher space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 88-94
-
- Article
- Export citation
Rational normal octavic surfaces with a double line, in space of five dimensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 95-102
-
- Article
- Export citation
Planar threefolds in space of four dimensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-115
-
- Article
- Export citation
The reflexion of light at a surface covered by a monomolecular film
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 116-130
-
- Article
- Export citation
Surface motion of sputtered particles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 131-135
-
- Article
- Export citation
Some observations on the theory of interchange of vibrational and translational energy
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 136-141
-
- Article
- Export citation
Asymptotic expansions of the expressions for the partition function and the rotational specific heat of a rigid polyatomic molecule for high temperatures
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 142-148
-
- Article
- Export citation
Some comments on the relation between ionisation and ionisation current in gases at high pressures
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 149-155
-
- Article
- Export citation
The upper limit of energy in the β-ray spectrum of actinium B
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 156-160
-
- Article
- Export citation
The equilibrium of atoms and ions adsorbed on a metal surface
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 161-164
-
- Article
- Export citation
Front matter
PSP volume 29 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 29 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation


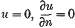 or similar, these conditions becoming identical at any part of the boundary of
or similar, these conditions becoming identical at any part of the boundary of 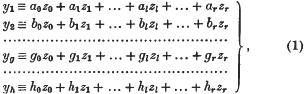

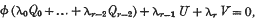
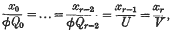
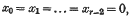
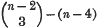 triple points.
triple points.
